Transformasi Geometri [Part 2] - Translasi (Pergeseran)
Summary
TLDRIn this educational video, Pak Beni explains the concept of translation (pergeseran) in geometry, focusing on how points and shapes shift on the Cartesian plane. Through visual and algebraic examples, viewers learn how to calculate translations along the x and y axes, using both drawings and formulas. The video covers practical examples, such as translating a triangle, determining translation vectors, and step-by-step coordinate transformations. It's an accessible introduction to a key geometric transformation, preparing viewers for further exploration of rotation in the next lesson.
Takeaways
- 😀 The video discusses the concept of translation (translasi) in geometry, focusing on moving points and shapes in a coordinate plane.
- 😀 Viewers are encouraged to understand how to determine the coordinates of a translated point or shape using either a diagram or formula.
- 😀 Translation is explained as a transformation that shifts every point of a geometric figure from one position to another.
- 😀 A simple example of translation is illustrated with two students pushing a table, demonstrating how objects shift in space.
- 😀 The translation formula is introduced, where the coordinates of a point P (x, y) shift by adding values to x and y, represented as A and B respectively.
- 😀 The significance of the translation direction is explained: positive values move right/up, while negative values move left/down.
- 😀 The example shows how to translate a triangle on a coordinate plane by moving each vertex according to specified units in the x and y directions.
- 😀 Viewers learn how to use the translation formula to calculate new coordinates for a triangle’s vertices after translation.
- 😀 Another example demonstrates how to find the translation needed to move a blue shape into a red shape by testing one point’s translation.
- 😀 A final example involves solving a translation problem by calculating the translation values for both x and y coordinates to map a point M to its new position M'.
Q & A
What is 'translasi' or translation in geometry?
-Translasi (translation) is a geometric transformation that shifts every point of a shape or object from one position to another, either horizontally or vertically.
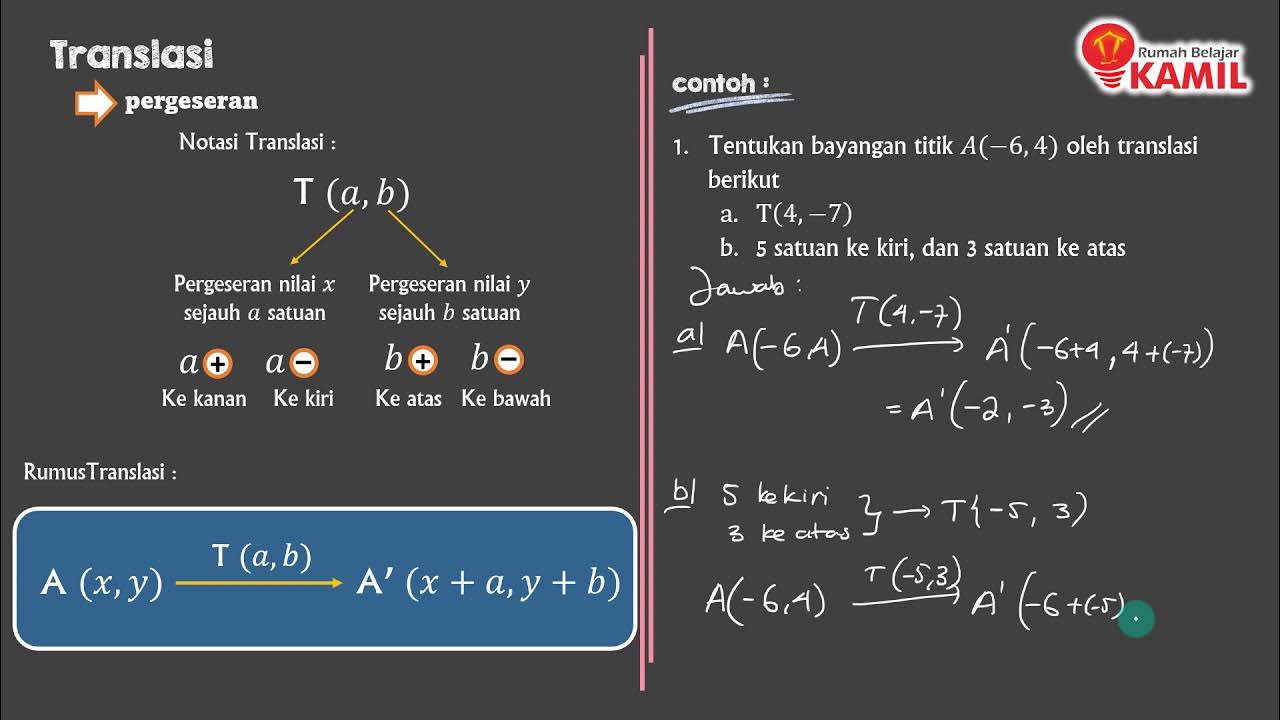
How does the translation formula work?
-The translation formula for a point P (x, y) involves shifting it by a translation vector (A, B), where the new coordinates become (x + A, y + B). A represents the horizontal shift and B represents the vertical shift.
What does a positive or negative value for A and B represent in the translation formula?
-If A is positive, the point shifts to the right; if A is negative, it shifts to the left. Similarly, if B is positive, the point moves up, and if B is negative, it moves down.
What is the first step when performing a translation on a geometric shape?
-The first step is to identify and locate the coordinates of each point or vertex of the shape before applying the translation.
In the example of translating a triangle, how do we find the new coordinates of the vertices?
-To find the new coordinates, we apply the translation to each vertex. For example, if a triangle is translated 4 units to the right and 3 units down, we add 4 to the x-coordinate and subtract 3 from the y-coordinate of each vertex.
Can we use the translation formula to solve translation problems visually or algebraically?
-Yes, the translation can be solved both visually by graphing the points and applying the shift, or algebraically by using the translation formula (x + A, y + B). Both methods should give the same result.
In the example where a triangle was translated, what were the final coordinates of the vertices?
-In the example, the final coordinates of the triangle's vertices after the translation were (1, 5) for A', (3, 1) for B', and (2, 5) for C'.
What is the concept of reverse translation, as seen in one of the examples?
-Reverse translation involves determining the translation vector that moves a shape from one position to another. By testing one point, we can calculate the translation vector (A, B) needed to map the original shape to its new position.
How is a translation that involves multiple steps, like first moving a point 3 units and then 4 units, handled?
-For a translation with multiple steps, such as first translating 3 units and then 4 units, we apply each translation sequentially, adjusting the coordinates step by step to find the final position of the point.
What are the key takeaways from the lesson on translation in geometry?
-The key takeaways are understanding the concept of translation as a shift of points in the coordinate plane, the use of the translation formula (x + A, y + B), and how to apply the translation either visually or algebraically to determine new coordinates.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Bangun Datar [Part 1] - Garis dan Sudut

Matematika Kelas 9 Bab 3 Transformasi Geometri - A. Translasi hal. 136 - 143 Kurikulum Merdeka
Matematika Kelas 9 : Transformasi Geometri (part 1 : Translasi)

Transformasi Geometri [Part 3] - Rotasi (Perputaran)

Kekongruenan dan Kesebangunan [Part 1] - Kekongruenan Bangun Datar

Kekongruenan dan Kesebangunan [Part 2] - Kekongruenan Dua Segitiga
5.0 / 5 (0 votes)
