Fixed Point Iteration Method Intuition | Numerical Methods

Summary

In this video, the fixed point method is explored as an open root-finding technique, similar to Newton's method. The process involves converting the function into a form where the root can be approximated by iterating with a function g(x), until the error is minimal. The example of solving for the root of the function f(x) = x³ + x - 0.5 demonstrates how to find the intersection point, called the fixed point. The method is explained step by step, emphasizing its iterative nature and the concept of convergence until the error falls below an acceptable threshold.

Takeaways

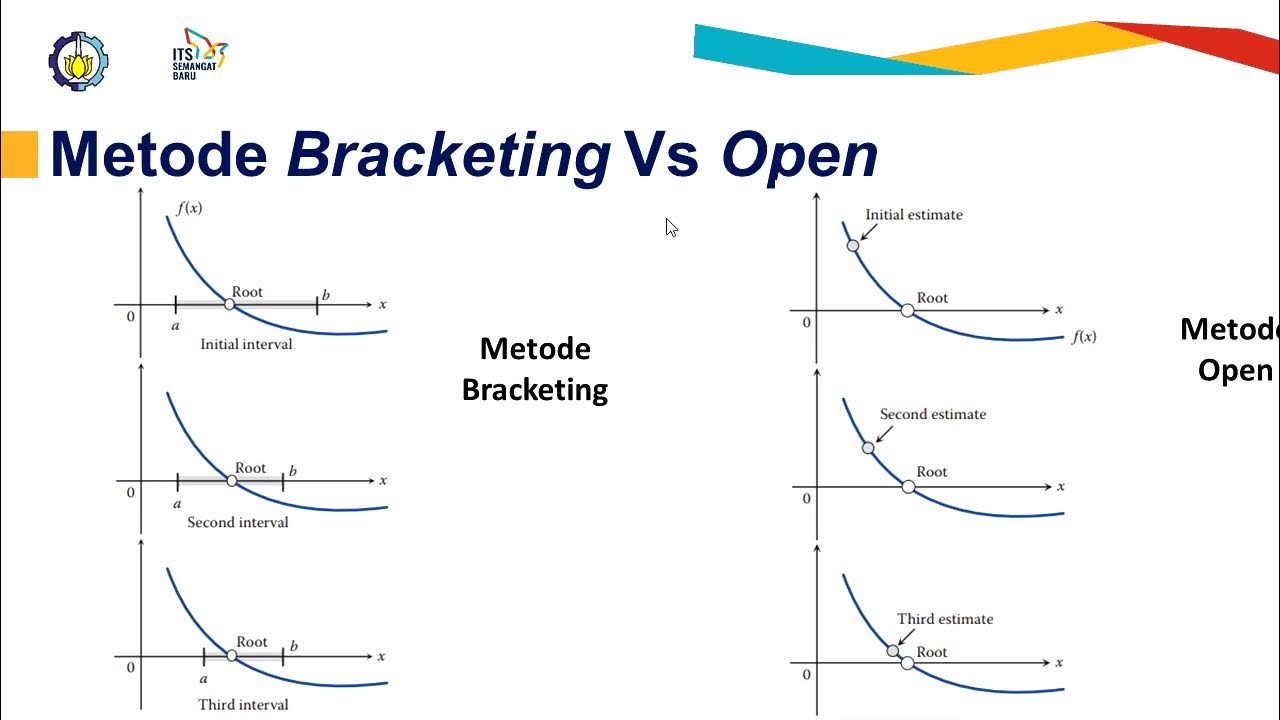
• 😀 The Fixed Point Method is an open root-finding technique used to approximate the solution to equations.
• 😀 The method is similar to other root-finding methods like Newton's Method.
• 😀 To solve for the root of a function, such as f(x) = x^3 + x - 0.5, the goal is to find when f(x) = 0.
• 😀 The fixed point method involves creating a function g(x) that represents the solution, where g(x) = x when f(x) = 0.
• 😀 The point where g(x) intersects with the x-axis is called the fixed point, where x = g(x).
• 😀 There are multiple valid ways to define g(x), which can give different approaches to solving for the root.
• 😀 The method involves iterating with an initial guess, updating x values using the equation g(x) = f(x) + x.
• 😀 In practice, we continue iterating until the difference between consecutive x values (error) is below a desired threshold.
• 😀 For example, starting with an initial guess of x = 0.1, we repeatedly update the value of x until the error is small enough.
• 😀 The error is calculated as the difference between the current x and the previous x value, and iterations stop once it meets the acceptable error level.
• 😀 The video suggests that further examples and explanations, including practical demonstrations in Excel or Google Sheets, will help clarify the method.

Q & A

What is the fixed point method used for?

The fixed point method is an open root finding technique used to approximate the roots of a function.

How is the fixed point method related to other root finding methods?

It is similar to other root finding methods, like Newton's method, in that it is used to find an approximate solution to the equation f(x) = 0.

What is meant by a function's 'root'?

A root of a function is the point where the function's output is zero, meaning f(x) = 0.

How do we find a root using the fixed point method?

We transform the function f(x) = 0 into a form g(x) = x, and then iteratively solve for x by plugging in values into g(x) until the values converge.

What does the graph of the fixed point method look like?

The graph typically shows the intersection of the transformed function g(x) with the line x = g(x), where the x-value at the intersection is the fixed point.

Why do we have multiple valid g(x) functions in the fixed point method?

We can derive different valid g(x) functions from f(x) by algebraically manipulating the equation, giving us multiple possible forms to apply in the fixed point method.

How does the fixed point method work algorithmically?

The algorithm iterates by taking an initial guess for x, applying it to g(x), and then refining the guess until the difference between consecutive guesses is below an acceptable threshold.

What is the error in the fixed point method?

The error is the difference between the current value of x and the next iteration of x. The process continues until this error is sufficiently small.

What role does the initial guess for x play in the fixed point method?

The initial guess for x is crucial, as it starts the iterative process. A good guess can lead to faster convergence, while a poor guess may require more iterations or fail to converge.

What are the potential challenges when applying the fixed point method?

Challenges include choosing an appropriate g(x) function, ensuring convergence, and dealing with cases where the method may not work due to poor initial guesses or unsuitable functions.