Reconocer una composición de funciones | Khan Academy en Español

Summary

このビデオでは、関数の合成の概念を復習し、合成関数の理解を深める方法を紹介しています。具体的には、関数 f(x) = 1 + x と g(x) = cos(x) を使って合成関数 f(g(x)) の作り方を解説しています。また、関数を合成する方法のいくつかのアプローチを示し、合成関数の理解を助けるために練習問題も提供されています。さらに、合成関数だけでなく、関数の積のような異なる関数の組み合わせにも触れ、さまざまなケースをカバーしています。

Takeaways

• 😀 関数の合成とは、1つの関数の出力を別の関数の入力として使うことを指します。
• 😀 例として、関数 f(x) = 1 + x と g(x) = cos(x) の合成 f(g(x)) を扱います。
• 😀 関数 f(x) の定義において x を g(x) に置き換え、f(g(x)) = 1 + cos(x) となります。
• 😀 合成の方法は、まず入力を別の関数に変え、その結果を元の関数に入力することです。
• 😀 g(x) = sin(x) + 1 のように複雑な関数も、他の簡単な関数の合成として表現できます。
• 😀 関数の合成は、場合によっては複数の関数に分解して理解することができます。
• 😀 例では、g(x) = cos(sin(x) + 1) を cos(x) と sin(x) の合成として扱う方法を示しました。
• 😀 合成関数を理解するには、関数の「入出力の流れ」を明確に追跡することが重要です。
• 😀 関数の積と合成の違いについても触れ、積の例として f(x) = cos(x) * sin(x) を挙げました。
• 😀 合成の重要性は、特に微積分、特に連鎖律を学ぶ際に大きな役割を果たします。

Q & A

関数の合成とは何ですか？

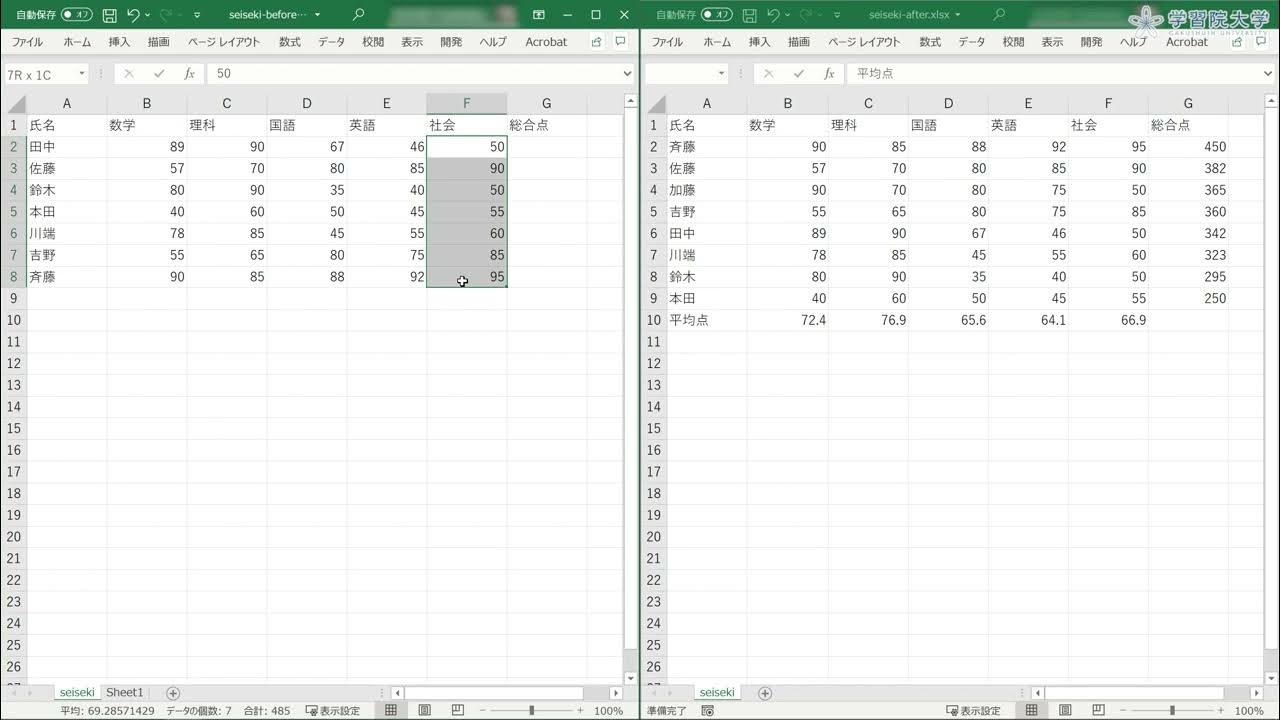
関数の合成とは、ある関数の出力を別の関数の入力として使用する操作です。例えば、f(g(x))のように、g(x)の結果をf(x)に入力することで、新しい関数が形成されます。

f(g(x))の計算手順はどのようになりますか？

まずg(x)を計算し、その結果をf(x)の入力として使用します。具体的には、f(g(x)) = 1 + cos(x)のように、f(x)の定義にg(x)を代入して求めます。

関数g(x)の例として、どのようなものがありますか？

例として、g(x) = sin(x) + 1のような関数があります。これを使って他の関数を合成することができます。

g(x) = sin(x) + 1を別の関数として分解する方法はありますか？

g(x) = sin(x) + 1は、例えばh(x) = sin(x)とi(x) = x + 1のように、2つの関数の合成として表現できます。これにより、g(x)を別の視点で理解することができます。

3つの関数を合成する例を示してください。

例えば、f(x) = cos(x), g(x) = sin(x) + 1, h(x) = cos(x)と定義し、f(g(h(x)))のように3つの関数を合成することができます。この場合、xを順番にh(x)、g(x)、f(x)に入れていきます。

関数の積と合成の違いは何ですか？

関数の積は、2つの関数を掛け合わせた結果を得る操作で、例えばf(x) = cos(x)とg(x) = sin(x)の場合、f(x) * g(x)のように計算されます。一方、合成はf(g(x))のように、1つの関数の結果を別の関数に入力する操作です。

関数の合成において、g(x)の定義が変更されると、結果はどう変わりますか？

g(x)の定義が変わると、合成された結果も変わります。例えば、g(x) = sin(x) + 1がg(x) = cos(x)に変われば、合成結果も異なった関数になります。

関数f(x) = cos(x) * sin(x)を合成関数として表現できますか？

f(x) = cos(x) * sin(x)は合成関数ではなく、2つの関数の積として表現できます。例えば、u(x) = cos(x)とv(x) = sin(x)として、f(x) = u(x) * v(x)のように定義されます。

関数合成を使う理由は何ですか？

関数合成を使うことで、複雑な操作を簡潔に表現することができます。特に、計算や解析が必要な場合、合成関数を使うことで問題を解決しやすくなります。

合成関数の具体的な応用例は何ですか？

合成関数は計算の効率化や、物理や工学などの分野で広く応用されます。例えば、速度と加速度の関係を表す式で、速度の関数に加速度を合成することで、全体の運動をモデル化することができます。