TEOREMA DE PITAGORAS Super Facil - Para principiantes
Summary
TLDRIn this video, Daniel Carrión explains the Pythagorean Theorem in a clear and engaging way, covering key concepts like right triangles, the hypotenuse, and the legs (catetos). He breaks down the process of squaring numbers and demonstrates how to apply the theorem to find missing sides of triangles through various examples. The video also provides exercises for viewers to practice their understanding of the theorem. With step-by-step explanations and relatable examples, this lesson helps viewers grasp an essential mathematical concept with ease.
Takeaways
- 😀 Pythagoras was a Greek philosopher and mathematician known for the Pythagorean theorem.
- 😀 A right triangle has one 90-degree angle, with the longest side being the hypotenuse.
- 😀 The other two sides of a right triangle are called the legs or catetos, and are denoted as a and b.
- 😀 Squaring a number means multiplying it by itself (e.g., 3² = 9, 4² = 16).
- 😀 The Pythagorean theorem states: (hypotenuse)² = (leg a)² + (leg b)².
- 😀 Example 1: A right triangle with legs of 3 cm and 4 cm has a hypotenuse of 5 cm (3² + 4² = 5²).
- 😀 Example 2: For a triangle with legs 6 cm and 5 cm, the hypotenuse is approximately 7.81 cm.
- 😀 To find an unknown hypotenuse, use the formula: c² = a² + b² and solve for c.
- 😀 To find an unknown leg, rearrange the formula to: a² = c² - b² or b² = c² - a².
- 😀 Example 3: Given a hypotenuse of 10 cm and leg b of 8 cm, the unknown leg a is 6 cm.
- 😀 Example 4: Given a hypotenuse of 15 cm and leg a of 12 cm, the unknown leg b is 9 cm.
Q & A
What is the Pythagorean theorem?
-The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It can be expressed as: a² + b² = c².
What is the meaning of the terms 'hypotenuse' and 'cathetus'?
-In a right-angled triangle, the 'hypotenuse' is the longest side, opposite the right angle, while the 'catheti' (plural of 'cathetus') are the two shorter sides that form the right angle.
How can you identify the hypotenuse in a triangle?
-To identify the hypotenuse, look for the angle of 90 degrees in the triangle. The side opposite this angle is the hypotenuse.
What does it mean to 'square' a number?
-To square a number means to multiply that number by itself. For example, 3 squared (3²) equals 3 * 3 = 9.
How do you apply the Pythagorean theorem to find an unknown side?
-To find an unknown side, you rearrange the Pythagorean theorem. If you know the hypotenuse and one cathetus, you subtract the square of the known cathetus from the square of the hypotenuse and then take the square root of the result.
Can you give an example of how the Pythagorean theorem works?
-Sure! If a triangle has catheti of lengths 3 and 4, and you need to find the hypotenuse, you would use the formula: 3² + 4² = c². That’s 9 + 16 = 25, so the hypotenuse is √25 = 5.
What is the result when you apply the Pythagorean theorem to a triangle with catheti of lengths 6 and 5?
-For a triangle with catheti of lengths 6 and 5, the hypotenuse can be found as follows: 6² + 5² = c². This gives 36 + 25 = 61. Taking the square root of 61, the hypotenuse is approximately 7.81.
How do you find a missing cathetus when the hypotenuse and the other cathetus are known?
-To find the missing cathetus, you rearrange the Pythagorean theorem: c² - a² = b². For example, if the hypotenuse is 10 cm and one cathetus is 8 cm, you would subtract 8² from 10², resulting in 100 - 64 = 36. The missing cathetus is the square root of 36, which is 6 cm.
What happens if the Pythagorean theorem doesn't hold true in a triangle?
-If the Pythagorean theorem doesn't hold true, then the triangle is not a right-angled triangle. The theorem specifically applies only to right-angled triangles.
Why is the Pythagorean theorem important in geometry?
-The Pythagorean theorem is fundamental in geometry because it relates the sides of a right-angled triangle in a precise way, which is useful for calculating distances, areas, and in real-world applications like construction and navigation.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie

Introdução ao Teorema de Pitágoras | Geometria | Khan Academy

Kurikulum Merdeka Matematika Kelas 8 Bab 2 Teorema Pythagoras
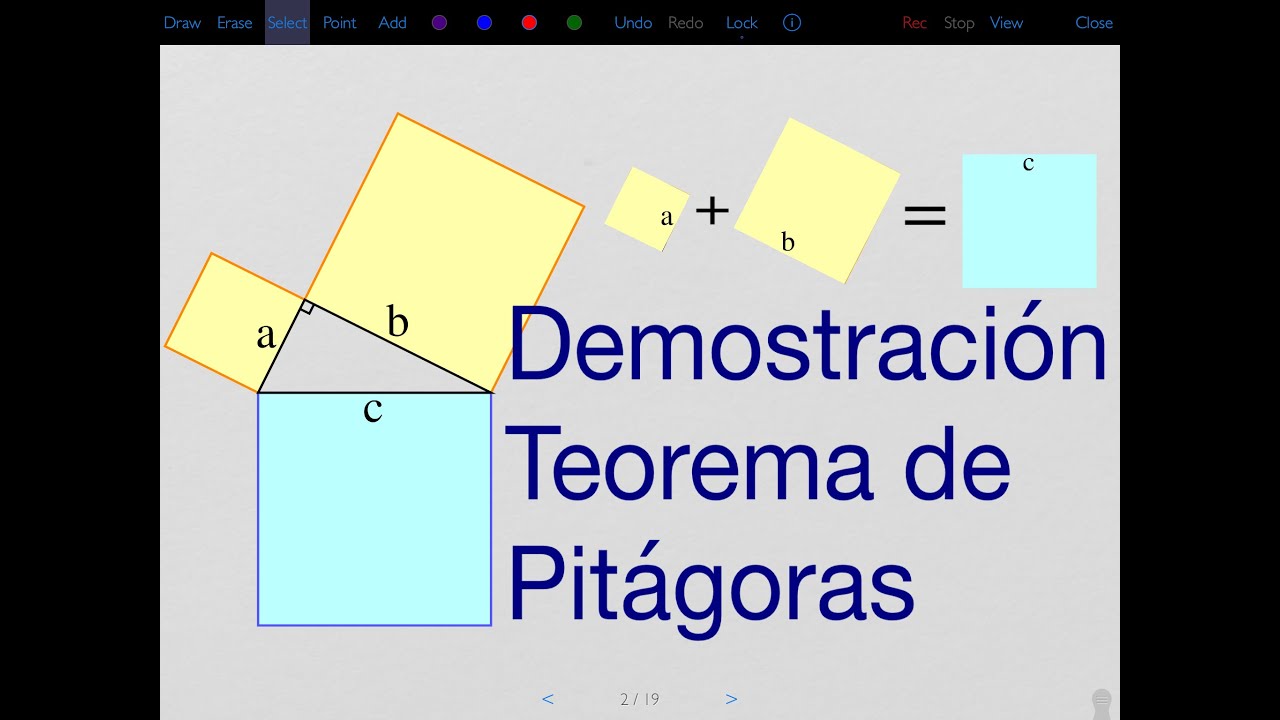
Demostración del teorema de Pitágoras

Kelas VIII - Apa itu Teorema Pythagoras?

Teorema Pythagoras [Part 1] - Menentukan Panjang Salah Satu Sisi Pada Segitiga Siku-siku
5.0 / 5 (0 votes)
