[SER222] M02_02 Algorithm Analysis (1/3): The Claim/Proof Formulation
Summary
TLDREn este video, el orador explica cómo analizar el número de comparaciones necesarias para ordenar un arreglo con el algoritmo Merge Sort de arriba hacia abajo. Comienza con una afirmación extraída del texto, que se propone probar mediante la construcción directa. La explicación cubre la definición de los casos base, la relación recursiva para calcular las comparaciones y los análisis de los mejores y peores casos. El objetivo es simplificar la relación recursiva en una fórmula cerrada que permita evaluar el rendimiento del algoritmo en términos de comparaciones.
Takeaways
- 😀 Se comienza con una afirmación de los autores del libro sobre el rendimiento de mergesort, que requiere entre N log N y N log N comparaciones para ordenar un arreglo de longitud N.
- 😀 Aunque sabemos que la afirmación es correcta, el objetivo es probarla y comprender por qué es cierta, no solo aceptarla como un hecho.
- 😀 El proceso de prueba de un algoritmo generalmente implica hacer suposiciones informadas sobre su funcionamiento, probar esas suposiciones, y refinar la hipótesis según sea necesario.
- 😀 Los algoritmos son frecuentemente analizados mediante una serie de conjeturas basadas en su estructura, como si contiene bucles o recursión, y luego se ajustan a medida que se prueba el rendimiento real.
- 😀 Se utiliza la técnica de 'construcción directa' para demostrar la afirmación, que consiste en construir la respuesta en lugar de utilizar métodos como la inducción o la contradicción.
- 😀 Se define C(N) como el número de comparaciones necesarias para ordenar un arreglo de tamaño N, que es el objetivo del análisis.
- 😀 La base del caso se establece como N = 0 y N = 1, donde no se requieren comparaciones porque los arreglos ya están ordenados.
- 😀 La parte recursiva de mergesort se modela mediante una recurrencia, donde C(N) depende de la cantidad de comparaciones necesarias para ordenar dos subarreglos de tamaño N/2 cada uno.
- 😀 Se establecen límites superior e inferior para el número de comparaciones posibles: el límite superior es N, y el límite inferior depende de la forma en que los subarreglos son intercalados durante el proceso de fusión.
- 😀 El caso más complicado es el peor caso, que ocurre cuando los subarreglos están perfectamente alternados, lo que maximiza las comparaciones en cada paso de fusión.
- 😀 Finalmente, se plantea que el siguiente paso es encontrar una solución cerrada para la recurrencia, con el objetivo de obtener una fórmula simple que describa el tiempo de ejecución de mergesort en lugar de depender de recursiones complejas.
Q & A
¿Cuál es la afirmación principal que se analiza en el video?
-La afirmación principal es que el algoritmo de Mergesort usa entre 'un medio N log N' y 'N log N' comparaciones para ordenar cualquier arreglo de longitud N.
¿Por qué el presentador dice que, aunque la afirmación es verdadera, aún es necesario demostrarla?
-El presentador afirma que aunque sabemos que la afirmación es cierta según el libro de texto, aún necesitamos demostrarla para entender cómo y por qué es verdadera, no solo aceptarla sin cuestionarla.
¿Qué técnica de prueba se utiliza en este video?
-Se utiliza la técnica de construcción directa, que consiste en construir una solución a partir de las definiciones y análisis del algoritmo.
¿Qué significa la función C(N) en el contexto de este análisis?
-C(N) representa el número de comparaciones necesarias para ordenar un arreglo de longitud N usando Mergesort.
¿Cómo se define el caso base de la recurrencia para el algoritmo?
-El caso base de la recurrencia se define para N igual a 0 y N igual a 1, donde no se requieren comparaciones porque los arreglos de longitud 0 o 1 ya están ordenados.
¿Qué implica la recurrencia que se establece para Mergesort?
-La recurrencia indica que el número de comparaciones necesarias para ordenar un arreglo de tamaño N es la suma de las comparaciones necesarias para ordenar dos subarreglos de tamaño N/2, más el costo de comparar y fusionar esos subarreglos.
¿Qué significa la parte de la recurrencia con 'C(floor(N/2))' y 'C(ceil(N/2))'?
-Las expresiones 'floor(N/2)' y 'ceil(N/2)' se usan para dividir el arreglo en dos subarreglos, manejando el caso en que N no es un número par, asegurando que los elementos no se cuenten dos veces.
¿Qué es lo que determina el número máximo de comparaciones en Mergesort?
-El número máximo de comparaciones ocurre cuando los dos subarreglos se alternan perfectamente, lo que garantiza que se hagan comparaciones en cada paso del proceso de fusión.
¿Por qué se consideran tanto los límites superior e inferior en la recurrencia?
-Se consideran tanto el límite superior como el inferior para analizar el caso de mayor cantidad de comparaciones (peor caso) y el caso con menor cantidad de comparaciones (mejor caso), aunque solo se demostrará el caso más relevante, que es el peor caso.
¿Qué es lo que falta por hacer después de establecer las recurrencias para C?
-Después de establecer las recurrencias para C, el siguiente paso es encontrar una solución cerrada para la recurrencia, es decir, una fórmula simple que represente el número total de comparaciones sin recurrir a una expresión recursiva.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
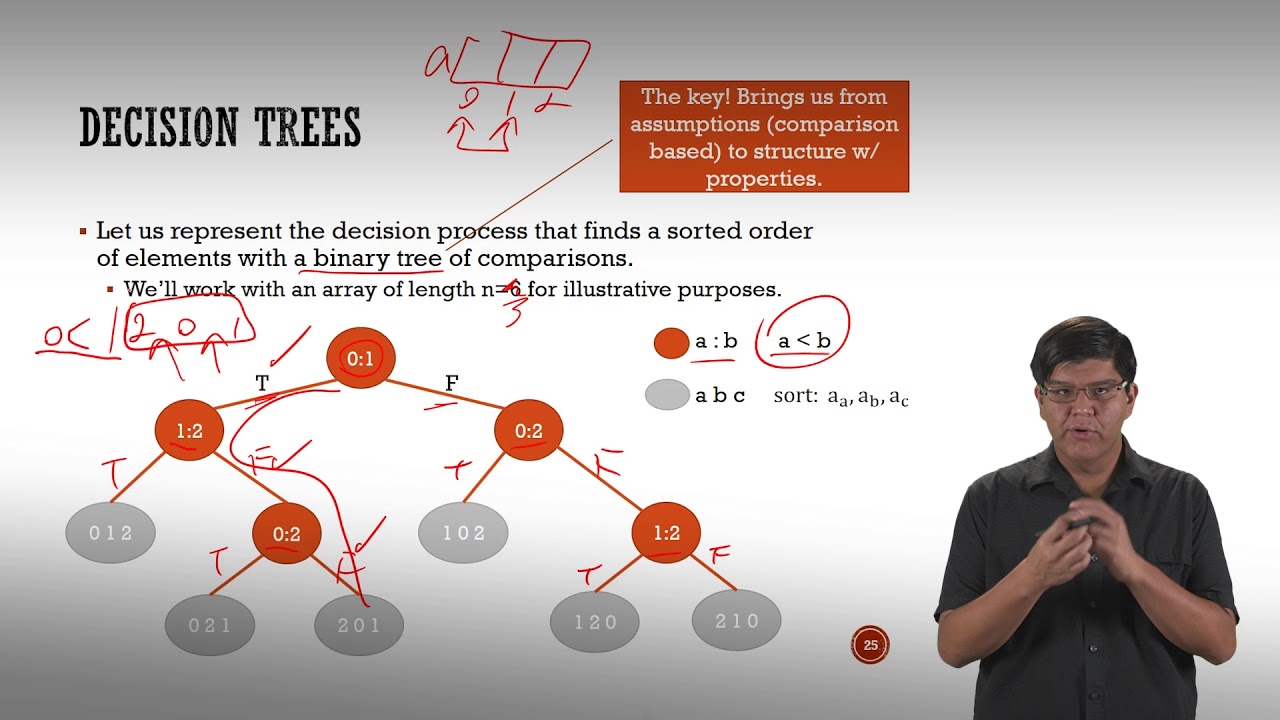
[SER222] M02_02 The Sorting Lower Bound (2/4): Decision Trees

[SER222] M02_02 The Algorithm (6/8): Implementation
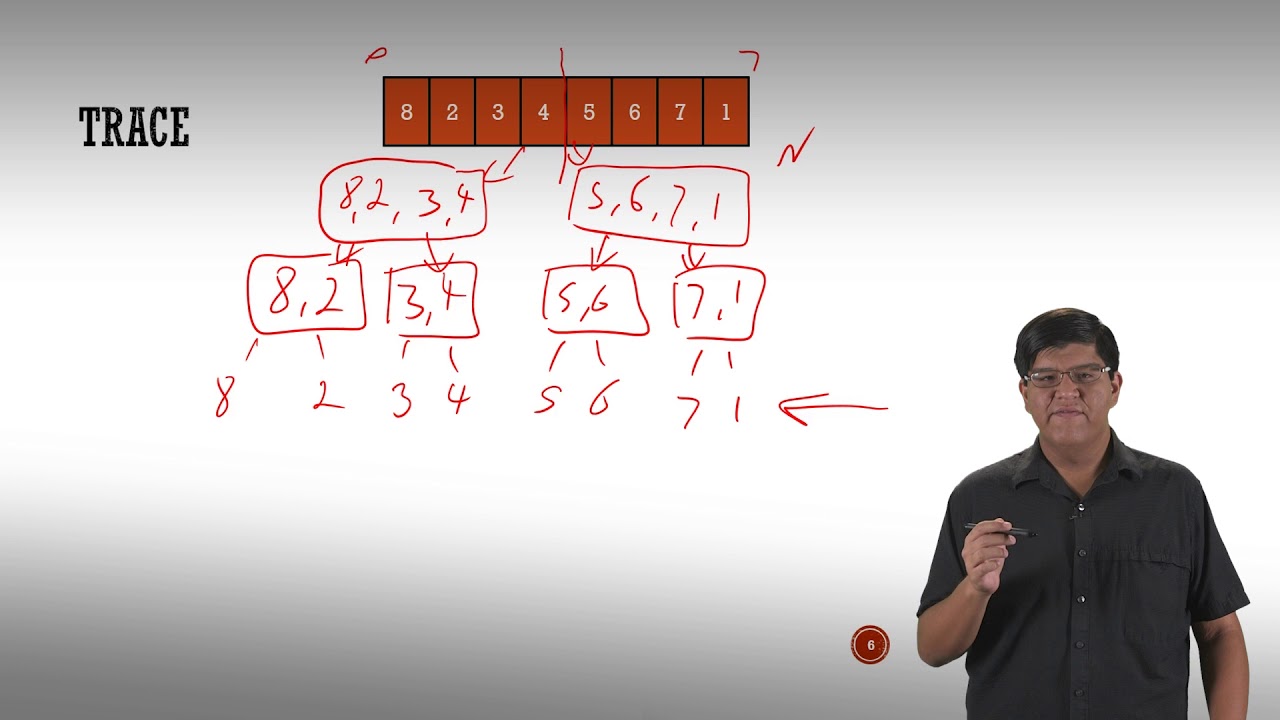
[SER222] M02_02 The Algorithm (4/8): Algorithm Trace

52. Programación en C++ || Ordenamientos || Ordenamiento por Selección

[SER222] M02_02 The Algorithm (7/8): Implementing Merge

Ordenamiento Quicksort (Rápido!) en Java
5.0 / 5 (0 votes)
