17 MULTIPLICAR Y DIVIDIR FRACCIONES ALGEBRAICAS
Summary
TLDREn este video se explican las operaciones de multiplicación y división de fracciones algebraicas, destacando su simplicidad en comparación con la suma y resta. Se demuestra cómo realizar estas operaciones utilizando la propiedad distributiva y se enfatiza la importancia de factorizar antes de operar, especialmente en casos de combinaciones de productos y divisiones. A través de ejemplos claros, se ilustra el proceso de simplificación de fracciones, resaltando la necesidad de identificar factores comunes en el numerador y el denominador para obtener el resultado final de manera efectiva.
Takeaways
- 😀 La multiplicación y la división de fracciones algebraicas son más sencillas que la suma y la resta.
- 😀 Para multiplicar, simplemente se multiplica el numerador por el numerador y el denominador por el denominador.
- 😀 En la división, se aplica el método de cruzar: el numerador de la primera fracción se multiplica por el denominador de la segunda.
- 😀 Es importante utilizar la propiedad distributiva al operar con polinomios.
- 😀 Factorizar los polinomios antes de operar facilita la simplificación de las fracciones.
- 😀 La factorización incluye reconocer productos notables, como suma por diferencia.
- 😀 En ejercicios complejos, es recomendable factorizar todos los términos antes de proceder con las operaciones.
- 😀 Al simplificar, se deben tachar los factores comunes del numerador y del denominador.
- 😀 Al final de las operaciones, se debe revisar si se puede simplificar aún más el resultado.
- 😀 El resultado final de las operaciones debe ser una fracción simplificada y no debe contener factores repetidos.
Q & A
¿Cuál es la ventaja de la multiplicación y división de fracciones algebraicas en comparación con la suma y resta?
-La ventaja es que la multiplicación y la división son más sencillas, ya que no requieren reducir a un mínimo común denominador.
¿Cómo se realiza el producto de dos fracciones algebraicas?
-Se multiplica el numerador por el numerador y el denominador por el denominador en línea.
¿Qué significa realizar una división de fracciones en cruz?
-En la división en cruz, se coloca el numerador de la primera fracción sobre el denominador de la segunda y viceversa.
¿Por qué es importante factorizar antes de operar con fracciones algebraicas?
-Es importante para simplificar las operaciones, lo que puede hacer que sean mucho más sencillas y menos propensas a errores.
¿Qué ejemplos se mencionan para factorizar los polinomios?
-Se mencionan ejemplos como suma por diferencia y diferencias de cuadrados para factorizar los numeradores y denominadores.
¿Qué se debe hacer con factores que se repiten en el numerador y el denominador?
-Se deben tachar para simplificar la fracción y reducirla a su forma más simple.
¿Cómo se aplican las propiedades distributivas en las operaciones con fracciones algebraicas?
-Se aplican al multiplicar los términos de los polinomios, tanto en el numerador como en el denominador.
¿Qué ocurre si se combinan varias multiplicaciones y divisiones?
-Se deben factorizar todos los términos antes de realizar las operaciones para evitar obtener polinomios de grado muy alto.
¿Qué factores se pueden cancelar en el ejemplo proporcionado?
-Se pueden cancelar los factores x + 2, x - 2 y x - 3 en el numerador y el denominador.
¿Cuál es el resultado final después de simplificar la expresión dada en el video?
-El resultado final es (x + 3) / (x - 3), que no se puede simplificar más.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
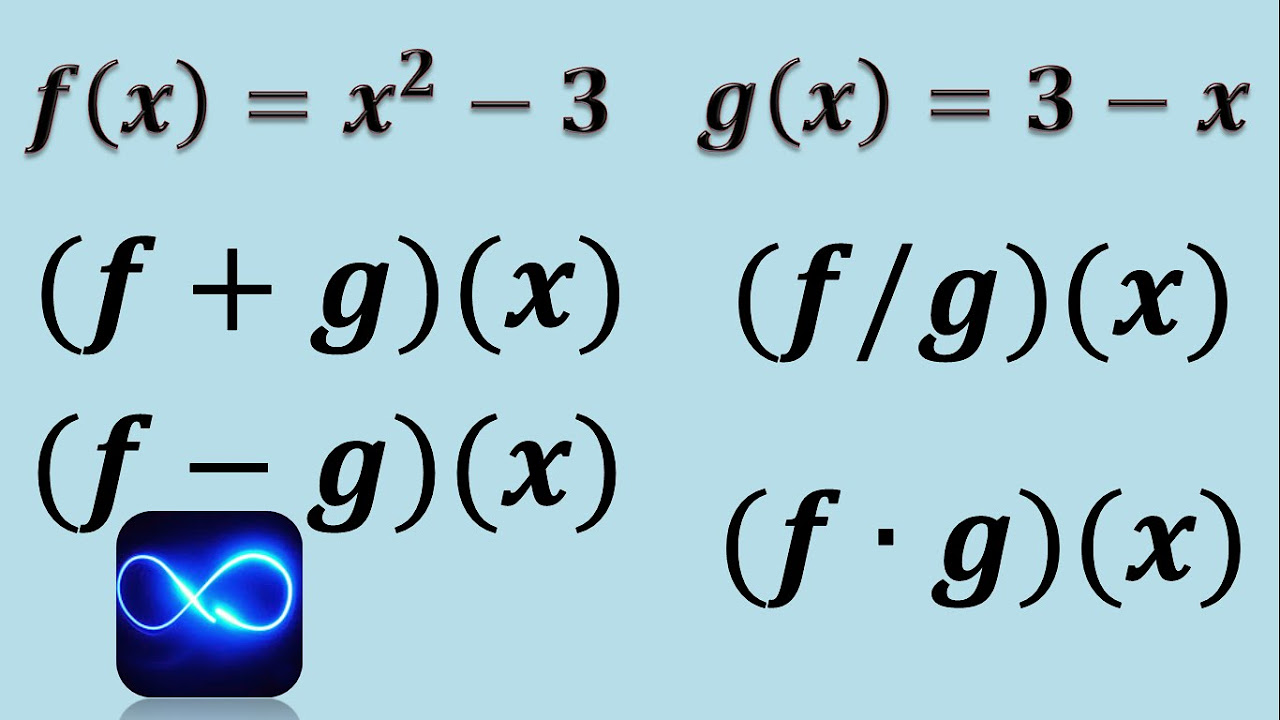
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)

Unidad 1 1.3 Expresiones Algebraicas Suma, Resta, Multiplicación y División

Pensamiento matemático 3. Progresión 3a. Suma de funciones
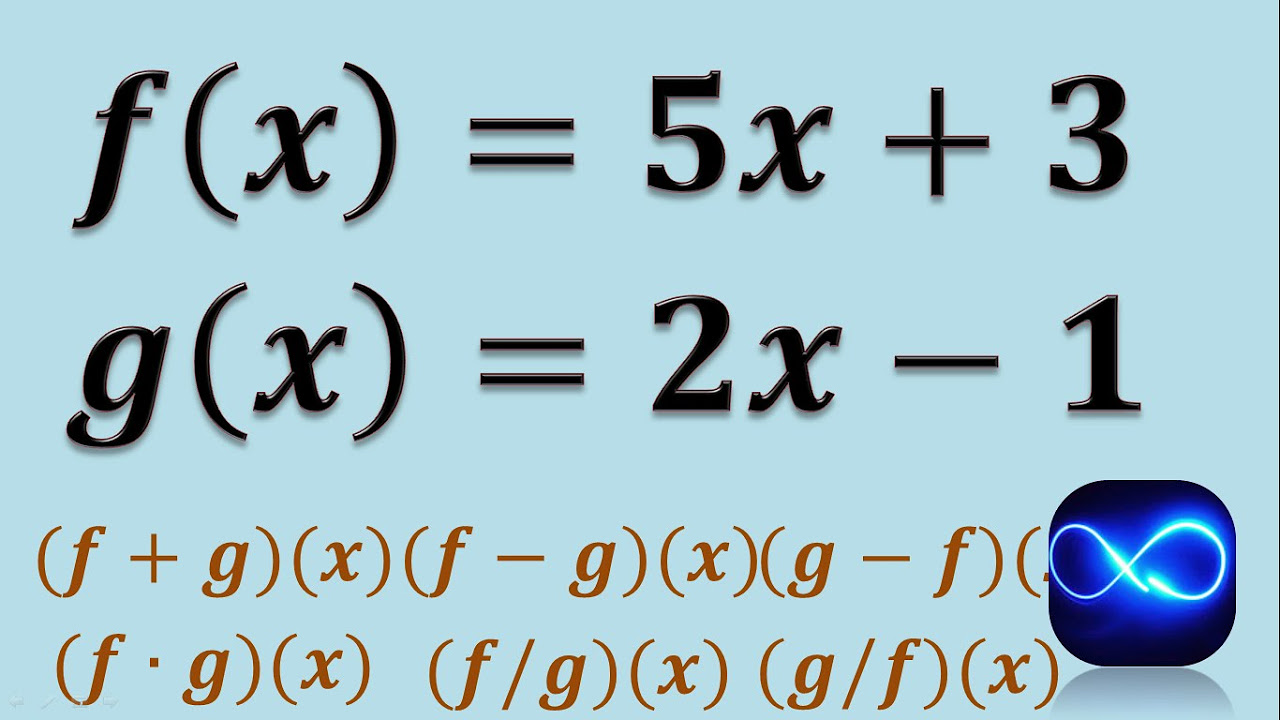
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 1)

TODAS las OPERACIONES con FRACCIONES desde Cero 🙀

Fracción y números decimales 4° Grado
5.0 / 5 (0 votes)
