Triangle Congruence Proofs Explained SSS, SAS, ASA, AAS, HL
Summary
TLDRThis video tutorial guides viewers through the process of performing two-column proofs to demonstrate triangle congruence, featuring five key criteria: SSS, SAS, ASA, AAS, and HL. The instructor emphasizes understanding given information as clues and systematically listing them in the proofs. Through detailed examples, viewers learn how to identify congruent angles and sides, apply properties like the reflexive property, and effectively structure their proofs. The tutorial aims to make the concepts more accessible, providing tips and techniques to simplify the learning experience for students struggling with this geometry topic.
Takeaways
- 😀 Understanding two-column proofs is essential for proving triangles congruent.
- 😀 There are five main methods for proving triangle congruence: SSS, SAS, ASA, AAS, and HL.
- 😀 Givens in a proof serve as clues to establish congruence relationships.
- 😀 Parallel lines create congruent angles when intersected by a transversal, useful in triangle proofs.
- 😀 The reflexive property states that any segment is congruent to itself, often used in proofs.
- 😀 Midpoints indicate that two segments are equal, providing crucial information for proofs.
- 😀 Vertical angles are always congruent, which can aid in establishing triangle congruence.
- 😀 It's important to list givens clearly at the beginning of your proof for clarity.
- 😀 When angles are bisected, the resulting segments are congruent, important for triangle relationships.
- 😀 The hypotenuse-leg theorem applies to right triangles, stating that if the hypotenuse and one leg are congruent, the triangles are congruent.
Q & A
What is the purpose of using two-column proofs in geometry?
-Two-column proofs are used to systematically show the logical steps that lead to proving triangles congruent, providing a clear and organized format.
What are the five methods for proving triangle congruence mentioned in the video?
-The five methods are Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), and Hypotenuse-Leg (HL).
How does knowing that lines are parallel help in triangle proofs?
-Parallel lines provide information about congruent angles formed by a transversal, which can be used in proofs to establish triangle congruence.
What is the reflexive property, and how is it used in triangle congruence?
-The reflexive property states that any segment or angle is congruent to itself, which helps establish congruence in shared sides or angles between triangles.
Why is it important to mark congruent segments and angles on the diagram?
-Marking congruent segments and angles on the diagram helps visualize the relationships and supports the proof process by keeping track of information.
What is the significance of the definition of midpoint in triangle proofs?
-The definition of midpoint indicates that two segments are congruent when a point divides another segment into two equal parts, which can be critical in establishing triangle congruence.
What does the Angle-Angle-Side (AAS) theorem state about triangle congruence?
-The AAS theorem states that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
What is the vertical angles theorem and its role in triangle proofs?
-The vertical angles theorem states that angles opposite each other when two lines intersect are congruent, which can be used to establish angle congruence in triangle proofs.
How does the hypotenuse-leg theorem apply specifically to right triangles?
-The hypotenuse-leg theorem states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and leg of another right triangle, then the triangles are congruent.
Why is it important to state the reasoning behind each step in a two-column proof?
-Stating the reasoning helps validate each step logically, showing how conclusions are reached and ensuring clarity and accuracy in the proof process.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

#kongruen Kongruensi (2) - Syarat dua segitiga kongruen - Matematika SMP kelas 9

Kekongruenan dan Kesebangunan [Part 2] - Kekongruenan Dua Segitiga

Triangle Congruence Theorems Explained: ASA, AAS, HL
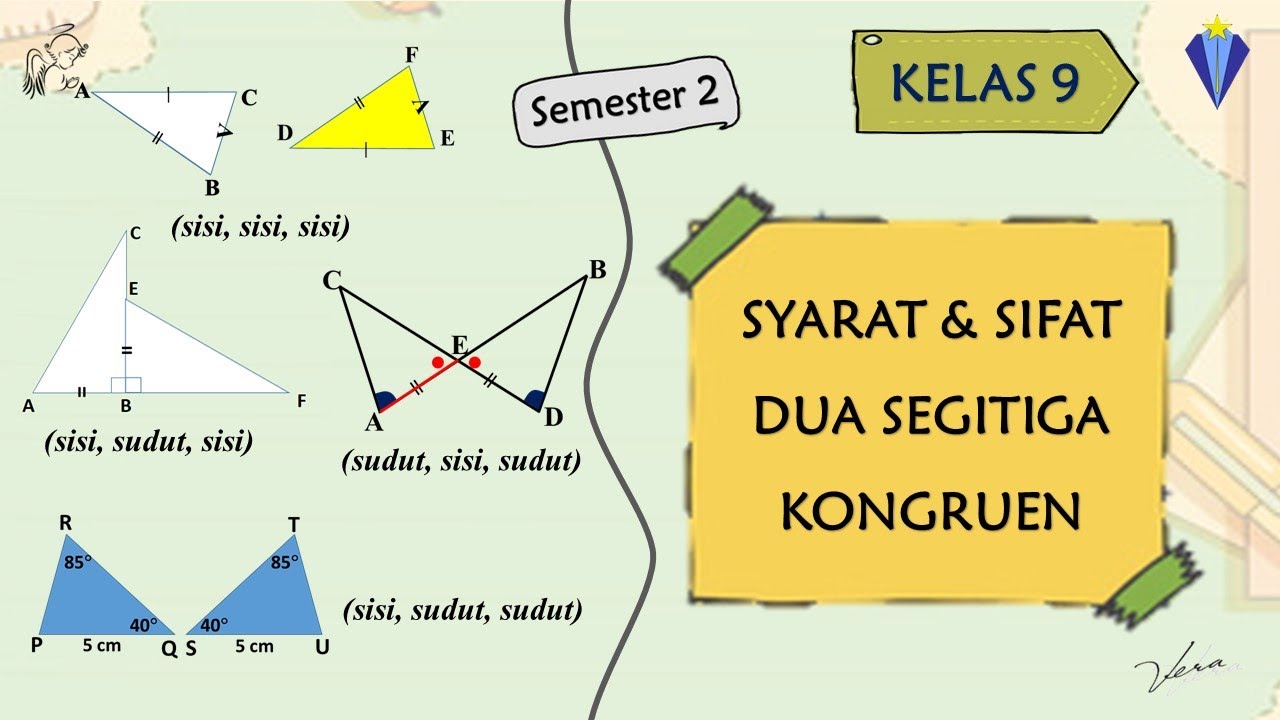
2 SYARAT DAN SIFAT DUA SEGITIGA KONGRUEN - KESEBANGUNAN DAN KONGRUENSI - KELAS 9 SMP

Geometry Chapter 5.5 Video

KEKONGRUENAN (Materi Kelas 9 SMP)
5.0 / 5 (0 votes)
