BUKU MATEMATIKA PKS GEMATAMA KELAS XI FASE F KURIKULUM MERDEKA MATERI OPERASI ALJABAR PADA FUNGSI
Summary
TLDRIn this educational video, the presenter explores the fundamental concepts of function algebra, focusing on operations such as addition, subtraction, multiplication, and division of functions. Using practical examples, the video clarifies the determination of domains for polynomial, rational, and irrational functions, emphasizing the importance of restrictions like non-zero denominators. The presenter also discusses how to graphically represent functions and their domains, providing viewers with essential skills to solve problems in function composition and inversion. This comprehensive guide is designed for students seeking to deepen their understanding of algebraic functions and their applications.
Takeaways
- 😀 The video discusses algebraic operations on functions, focusing on defining two functions, f and g, on a common domain.
- 😀 The first algebraic operation is the sum of two functions, expressed as f + g, which combines their outputs over the intersection of their domains.
- 😀 The second operation is the difference of functions, f - g, which also shares the same domain requirement as their sum.
- 😀 Scalar multiplication of a function kf is explained, where the domain remains the same as that of the original function f.
- 😀 The product of two functions f and g is introduced, with the domain being the intersection of their respective domains.
- 😀 The division of functions f and g highlights the restriction that the denominator cannot be zero, influencing the domain accordingly.
- 😀 When determining the domain of polynomial functions, it is noted that they are defined for all real numbers.
- 😀 Rational functions are analyzed to ensure the denominator does not equal zero, specifying their domain restrictions.
- 😀 The script illustrates the domain of irrational functions, requiring that the expression inside the root is non-negative.
- 😀 Several examples are provided to apply these concepts practically, reinforcing the understanding of function operations and their domains.
Q & A
What are the main operations of algebra on functions discussed in the transcript?
-The main operations discussed include addition, subtraction, multiplication, and division of functions, as well as operations with scalar multiplication.
How is the domain of the sum of two functions determined?
-The domain of the sum of two functions f and g is the intersection of the domains of f and g.
What is the domain of a polynomial function?
-The domain of a polynomial function is all real numbers.
What conditions must be met for the domain of a rational function?
-For a rational function, the denominator cannot be zero, which means any value that makes the denominator zero is excluded from the domain.
How can the domain of an irrational function be determined?
-The domain of an irrational function, such as one involving a square root, includes all values for which the expression inside the root is greater than or equal to zero.
What is the process for finding the domain of a composite function?
-To find the domain of a composite function, you must consider the domain of the outer function and ensure that the input to the outer function is within the domain of the inner function.
What is the significance of the intersection of domains when performing operations on functions?
-The intersection of domains is crucial because it ensures that the resulting function from operations like addition or subtraction is defined for the common input values of the original functions.
In the context of functions, what does it mean to have a 'scalar' multiplication?
-Scalar multiplication involves multiplying a function by a constant value, affecting the output of the function but not its domain.
What is a key consideration when determining the domain of a function that is a ratio of two functions?
-A key consideration is to ensure that the denominator does not equal zero, which can lead to undefined values.
How does one find the domain of a function that includes a square root?
-To find the domain of a function that includes a square root, set the expression inside the square root greater than or equal to zero and solve for x.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Pembahasan materi FUNGSI (Domain & Range, Komposisi, Invers) KELAS 10 | #MatematikAsik

ATURAN DASAR OPERASI MATEMATIKA

ALJABAR PART 1 (PENJUMLAHAN DAN PENGURANGAN)

OPERAÇÕES: ADIÇÃO, SUBTRAÇÃO, MULTIPLICAÇÃO E DIVISÃO | MATEMÁTICA BÁSICA #2 | Prof. Diego Viug

GCSE Python #2: Arithmetic Operations
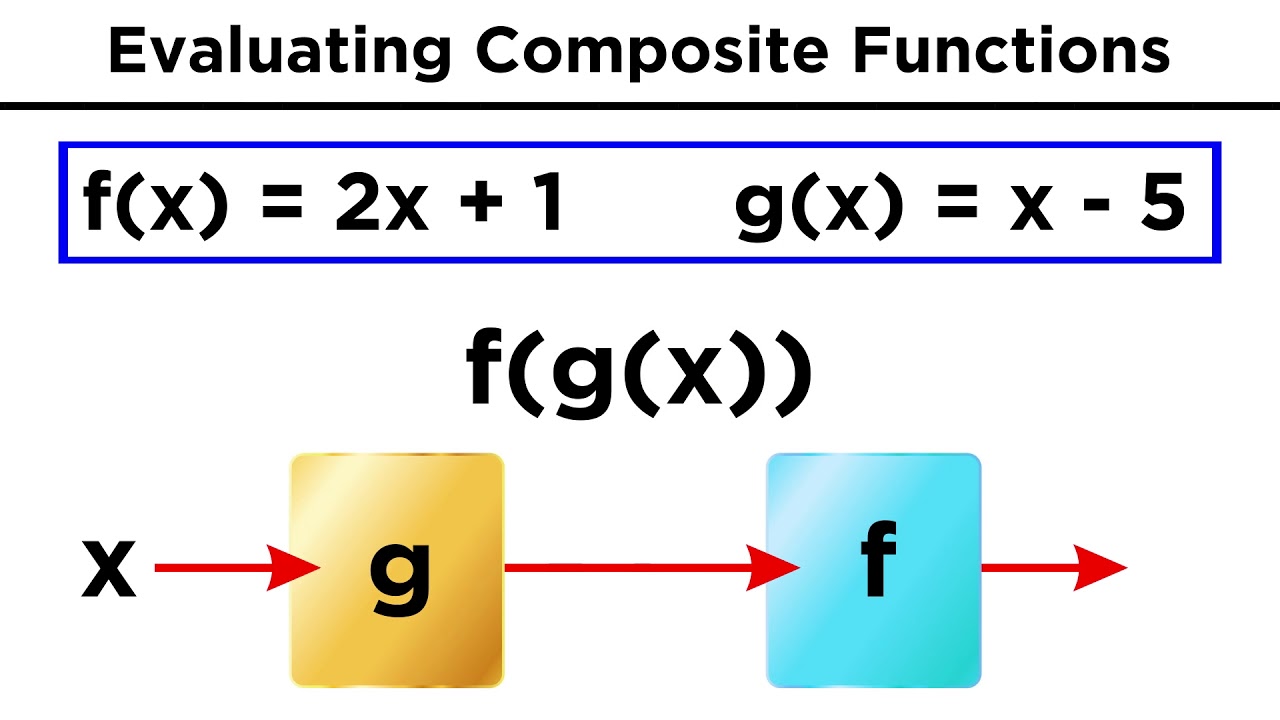
Manipulating Functions Algebraically and Evaluating Composite Functions
5.0 / 5 (0 votes)
