1 Obtener Función de Transferencia | Ejercicio Paso a Paso
Summary
TLDREn este tutorial, se aborda el proceso de derivación de la función de transferencia a partir de una ecuación diferencial que representa un sistema dinámico. A través de la transformada de Laplace, el instructor explica cómo convertir la ecuación del dominio del tiempo al dominio de la frecuencia, facilitando su manipulación algebraica. Se detallan las propiedades de la transformada aplicadas a cada término de la ecuación, eliminando las condiciones iniciales al establecerlas en cero. El video culmina con la presentación de la estructura de la función de transferencia, estableciendo una base para entender el comportamiento del sistema ante diferentes entradas.
Takeaways
- 😀 Se presentó un ejercicio para obtener la función de transferencia a partir de una ecuación diferencial en sistemas dinámicos.
- 📊 La ecuación incluye la segunda derivada, la primera derivada y la variable de estado, lo que es común en la modelación de sistemas.
- 🔄 Se utiliza la notación de derivadas con puntos para simplificar la representación de la ecuación.
- 📏 La transformada de Laplace se aplica para convertir la ecuación diferencial en el dominio del tiempo a una ecuación algebraica en el dominio de 's'.
- 📋 Se explicaron las propiedades de la transformada de Laplace, incluyendo la suma y el manejo de constantes multiplicativas.
- 🔍 Para las derivadas, se utilizaron fórmulas específicas que relacionan las transformadas de las derivadas con las condiciones iniciales.
- 🧮 Se destacó la importancia de establecer condiciones iniciales iguales a cero al calcular la función de transferencia.
- 🔗 La manipulación algebraica de la ecuación transformada permite identificar términos comunes y facilitar el despeje de la variable de salida.
- ⚙️ La función de transferencia se presenta como la relación entre la salida y la entrada en el dominio de Laplace.
- 💡 El ejercicio es una introducción a la modelación de sistemas, sentando las bases para estudios más avanzados en control y dinámica.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo principal del video es resolver un ejercicio para obtener la función de transferencia de una ecuación diferencial que representa un sistema dinámico.
¿Qué notación se utiliza para representar las derivadas en el ejercicio?
-Se utiliza una notación donde las derivadas se representan con puntos: la segunda derivada como 'x''', la primera como 'x'' y la función original como 'x(t)'.
¿Qué ecuación diferencial se utiliza como base en el ejercicio?
-La ecuación diferencial utilizada es: 3 por la segunda derivada de x(t) más 5 por la primera derivada de x(t) más x(t) igual a u(t).
¿Qué es la transformada de Laplace y por qué es importante en este contexto?
-La transformada de Laplace es una herramienta matemática que convierte funciones del tiempo en funciones de una variable compleja, lo que facilita el análisis de sistemas dinámicos al convertir ecuaciones diferenciales en ecuaciones algebraicas.
¿Cuáles son algunas propiedades de la transformada de Laplace que se aplican en el ejercicio?
-Se aplican propiedades como la linealidad, que permite sumar las transformadas de funciones, y las fórmulas para las transformadas de derivadas, que involucran las condiciones iniciales.
¿Qué resultado se obtiene al aplicar la transformada de Laplace a la ecuación diferencial?
-Al aplicar la transformada de Laplace, se obtiene una ecuación algebraica en términos de X(s) y U(s), donde se puede factorizar X(s).
¿Qué condiciones iniciales se asumen para simplificar el ejercicio?
-Se asumen condiciones iniciales iguales a cero: x(0) = 0 y la derivada x'(0) = 0, lo que simplifica el cálculo de la función de transferencia.
¿Cómo se expresa la función de transferencia al final del ejercicio?
-La función de transferencia se expresa como H(s) = X(s)/U(s) = 1/(3s² + 5s + 1).
¿Cuál es la importancia de la función de transferencia en sistemas dinámicos?
-La función de transferencia es crucial para entender cómo un sistema responde a entradas específicas, permitiendo predecir su comportamiento y diseñar controles adecuados.
¿Qué se sugiere hacer después de comprender este ejercicio?
-Se sugiere continuar explorando ejercicios más complejos para profundizar en la comprensión de los conceptos de sistemas dinámicos y el uso de la transformada de Laplace.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

FUNCIÓN, pendiente de la función en un punto P. Ecuación de la recta tangente en el punto P1(X1,Y1).

Cálculo integral, aplicación en crecimiento de plantas
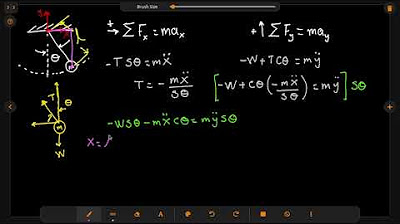
Modelado matemático de péndulo simple

DÉTECTION DE FUITES DE PIPELINE -Equation différentielle -MATLAB

ESTABILIDAD DE SISTEMAS - LUCIO ELÉCTRICO
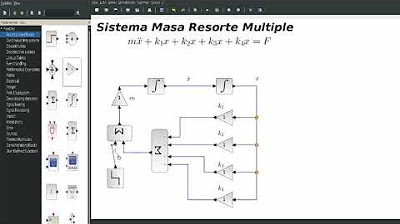
Simulación Sistema Masa Resorte Multiple XCos Part1
5.0 / 5 (0 votes)
