GCSE Maths - How to find the Area and Circumference of a Circle (Circles Part 1) #106
Summary
TLDRIn this educational video, viewers learn how to find the circumference and area of a circle by understanding key terms such as circumference, diameter, and radius. The video explains essential formulas, including A = πr² for area and C = 2πr or C = πd for circumference. Two practical examples illustrate the calculations using a radius of 4 cm and a diameter of 10 cm, showcasing the step-by-step process to arrive at the results. The video concludes with a call to action, encouraging viewers to like, subscribe, and visit their website for more resources.
Takeaways
- 😀 The circumference of a circle is the curved line forming its outer boundary.
- 😀 The diameter is a straight line passing through the center of the circle, connecting two points on its boundary.
- 😀 The radius is half the diameter, extending from the center of the circle to the circumference.
- 😀 Circumference is represented by 'C', diameter by 'D', and radius by 'r'.
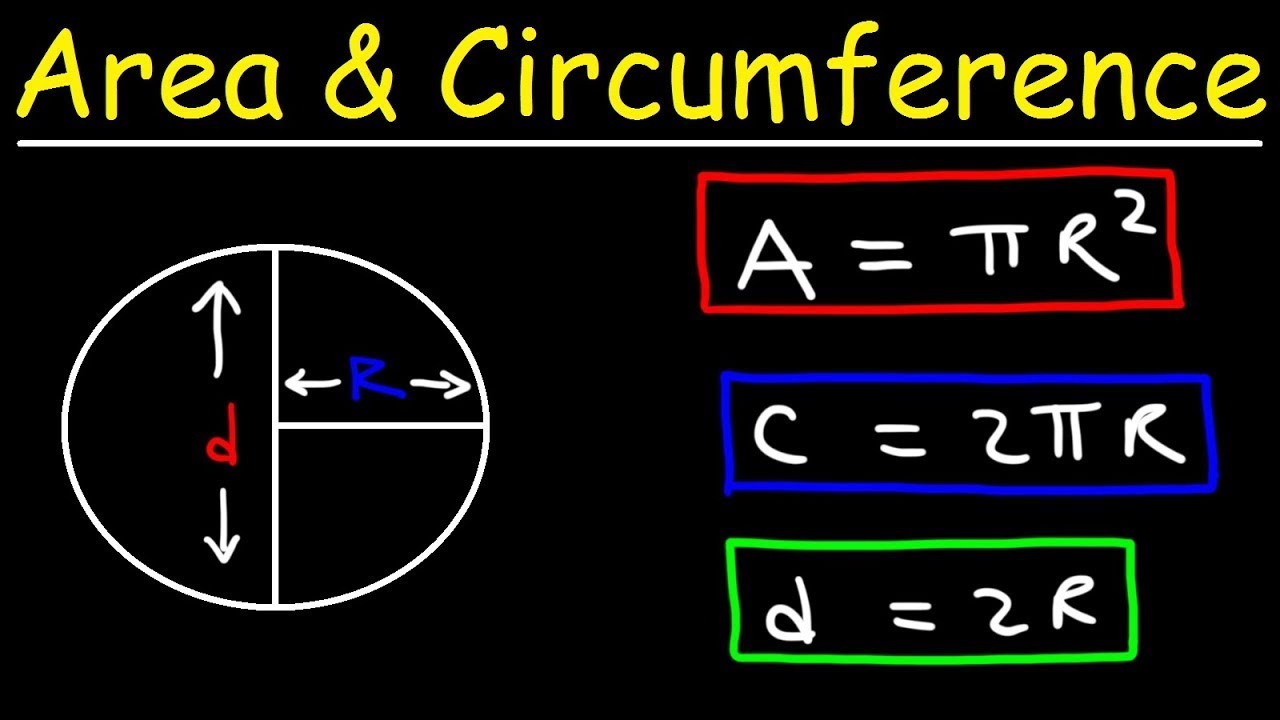
- 😀 The area of a circle is calculated using the formula A = πr².
- 😀 The circumference can be calculated with either C = 2πr or C = πd.
- 😀 Both formulas for circumference are equivalent, as diameter (d) is twice the radius (r).
- 😀 For a circle with a radius of 4 cm, the area is approximately 50.3 cm².
- 😀 The circumference for the same circle is approximately 25.1 cm.
- 😀 If given the diameter of 10 cm, the radius is calculated as 5 cm, leading to an area of 78.5 cm² and a circumference of 31.4 cm.
Q & A
What are the key terms associated with circles discussed in the video?
-The key terms are circumference, diameter, and radius.
How is the circumference of a circle defined?
-The circumference is the curved line that makes up the outside boundary of the circle.
What is the difference between the diameter and the radius?
-The diameter is a straight line that passes through the center of the circle, connecting two points on its boundary, while the radius is a straight line from the center to the circumference, which is half the diameter.
What is the formula for calculating the area of a circle?
-The formula for the area of a circle is A = πr², where r is the radius.
What are the two formulas for calculating the circumference of a circle?
-The two formulas for circumference are C = 2πr (using the radius) and C = πd (using the diameter).
If the radius of a circle is 4 cm, how do you calculate its area?
-To calculate the area, use the formula A = πr². Plugging in the radius: A = π × 4² = π × 16 ≈ 50.3 square centimeters.
How is the circumference calculated if the radius is 4 cm?
-Using the formula C = 2πr, the circumference is C = 2 × π × 4 = 25.1 centimeters.
What is the relationship between diameter and radius?
-The diameter is twice the length of the radius. If you have the radius, you can find the diameter by multiplying by 2.
What area does a circle with a diameter of 10 cm have?
-First, find the radius (which is 5 cm). Then use the formula A = πr²: A = π × 5² = 78.5 square centimeters.
How do you find the circumference of a circle when you know the diameter?
-Using the formula C = πd, for a diameter of 10 cm, the circumference is C = π × 10 = 31.4 centimeters.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
Circles - Area, Circumference, Radius & Diameter Explained!

Cara Mencari Keliling dan Luas Lingkaran Jika Jari-jari dan Diameter Diketahui

Cara Menghitung LUAS dan KELILING Lingkaran

How to Calculate Circumference of a Circle (Step by Step) | Circumference Formula

Radius & diameter from circumference | High School Geometry | High School Math | Khan Academy
Circumference and area of a circle - exact answers in terms of pi
5.0 / 5 (0 votes)
