Information entropy | Journey into information theory | Computer Science | Khan Academy
Summary
TLDR在本视频中,讲解了香农信息论中的一个重要概念——熵。通过两台机器的例子,比较了随机生成符号的机器与按概率分布生成符号的机器的不同信息量。熵是度量信息不确定性的量,反映了预测下一符号所需的最少问题数。视频通过举例和类比,展示了不同概率分布对信息量的影响,并解释了熵如何帮助量化信息或惊讶感。
Takeaways
- 😀 机器一以随机方式生成符号,每个符号的出现概率为25%。
- 😀 机器二的符号生成概率不同,A的出现概率为50%,其他符号的概率分别较低。
- 😀 信息的度量是基于不确定性(entropy),也可以通过“提问次数”来表示。
- 😀 机器一的输出需要平均两次‘是/否’问题来确定符号。
- 😀 机器二的输出平均需要1.75次‘是/否’问题,因其概率分布不均匀。
- 😀 Shannon通过模拟实验将问题转化为“弹跳”模型来解释符号生成过程。
- 😀 在机器一中,每个符号的出现概率相等,因此不确定性最大。
- 😀 机器二的输出符号概率不均,导致不确定性(entropy)低于机器一。
- 😀 Shannon定义的熵(entropy)是信息量的量度,衡量不确定性或惊讶感。
- 😀 熵的计算公式为:H = - Σ p(x) * log2 p(x),其中p(x)是符号x的概率。
- 😀 当所有输出符号的概率相等时,熵达到最大;如果输出变得可预测,熵将降低。
Q & A
什么是熵?
-熵是信息的平均不确定性或惊讶程度。它衡量了在预测下一个符号时需要提出的问题数量。熵越高,意味着预测越困难。
Shannon 如何定义信息单位?
-Shannon 定义了信息单位为“比特”(bit),它对应于公平的二元选择问题,如硬币翻转的结果。
机器一(Machine One)如何生成符号?
-机器一通过随机生成四个符号(A、B、C、D),每个符号的出现概率都是 25%。
机器二(Machine Two)如何生成符号?
-机器二生成符号的概率是不同的,符号 A 出现的概率为 50%,而符号 B 和 C 的概率合计为 25%,符号 D 的概率为 25%。
如何计算从机器一获取符号所需的最小问题数?
-对于机器一,由于每个符号的出现概率相等,最有效的方式是通过两次问题来区分符号。第一次可以将符号分成两组,第二次确定最终符号。
机器二的符号预测问题如何不同于机器一?
-机器二的符号预测由于符号出现概率不等,第一问可以确定符号 A 是否出现,如果没有,则通过第二问确定符号 D,最后通过第三问确定符号 B 或 C。
机器一和机器二需要多少个问题来预测符号?
-机器一需要 2 个问题来预测符号,而机器二平均需要 1.75 个问题。
如何计算机器二的平均提问数?
-通过加权平均计算,符号 A 的概率乘以 1 次提问,符号 B 和 C 的概率乘以 3 次提问,符号 D 的概率乘以 2 次提问,得到 1.75 次提问。
什么是香农的熵公式?
-香农的熵公式是每个符号的概率乘以该符号的出现概率的对数值(以 2 为底),然后求和。公式为:H = Σ(p(x) * log2(1/p(x)))。
熵的最大值发生在什么情况下?
-当所有可能的符号出现的概率相等时,熵达到最大值。也就是说,当所有符号出现的概率均为 25% 时,熵最大。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Andrew Briggs - Is Information the Foundation of Reality?

Lecture 6: Noisy Channel Coding (I): Inference and Information Measures for Noisy Channels

Hibridación del carbono

Nuxt Instance Unavailable - Async Code in Vue and Nuxt with the Composition API (+ raffle 🎁)

Physics of TIME and the SUPERNATURAL [PART 2]

Best Note-Taking & Personal Knowledge Management (PKM) Setup for Busy Professionals
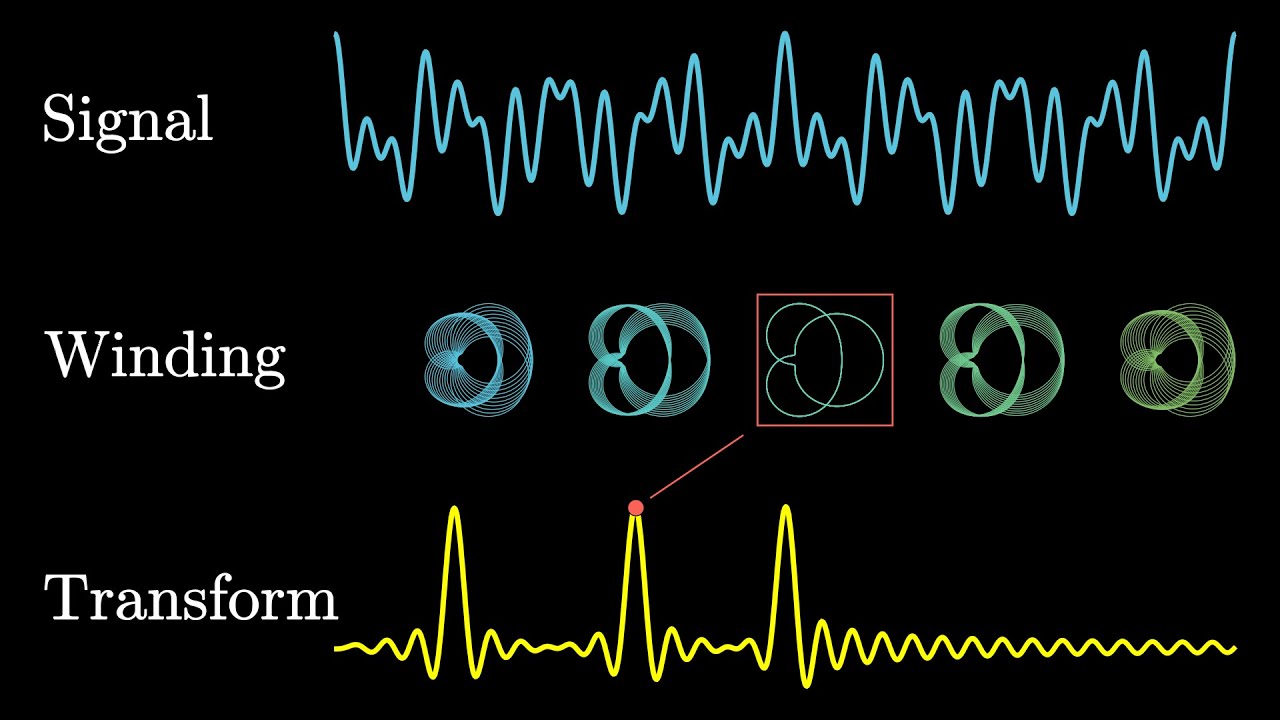
But what is the Fourier Transform? A visual introduction.
5.0 / 5 (0 votes)