Discrete Mathematics | Overview & Concept Of SET Theory By Dr.Gajendra Purohit

Summary

This educational video delves into set theory concepts, focusing on intersections, Cartesian products, and set differences. The instructor provides clear explanations and proofs to demonstrate how elements belong to set intersections and the implications of set differences. Key principles are illustrated through examples, emphasizing logical reasoning and problem-solving techniques. The session aims to enhance students' understanding of these foundational topics while encouraging further exploration through additional resources. Overall, the video is an engaging and informative resource for anyone looking to strengthen their grasp of set theory in mathematics.

Takeaways

• 😀 Understanding the intersection of sets is crucial for grasping how elements belong to multiple sets simultaneously.
• 🤔 If an element belongs to both set A and set B, it will also belong to their intersection, reinforcing the need to visualize set relationships.
• 📚 Proof techniques are important in set theory; demonstrating how elements fit within intersecting sets aids comprehension.
• 🔄 The difference between sets (e.g., B - A) indicates elements present in one set but not in another, clarifying set memberships.
• 🔍 Real-life examples help illustrate complex set interactions, making theoretical concepts more accessible.
• 🚫 If an element is part of the difference of two sets, it implies that the element cannot be part of the first set, emphasizing exclusion.
• 🔁 The discussion of empty sets highlights their role in set theory and their impact on intersection operations.
• 💡 The speaker encourages students to actively engage with set theory and related mathematical concepts for a deeper understanding.
• 📺 Additional resources are available for further learning, indicating the importance of continued education beyond the lecture.
• 🎓 The speaker promotes a community for learners to interact, share ideas, and deepen their mathematical knowledge.

Q & A

What is the primary focus of the lecture?

The primary focus of the lecture is on set theory, specifically the concepts of set intersections, differences, and the relationships between elements in various sets.

How is the intersection of two sets defined?

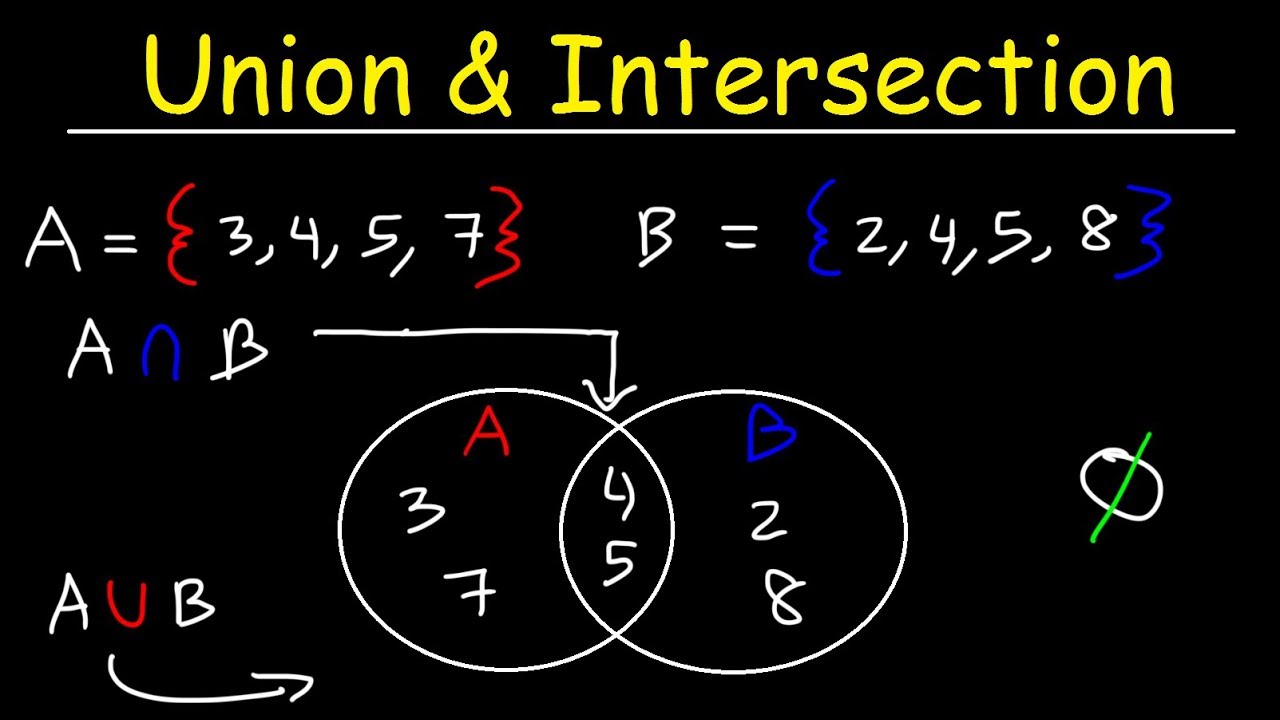
The intersection of two sets, denoted as A ∩ B, consists of all elements that are common to both sets A and B.

What does the notation A - B represent?

The notation A - B represents the difference between sets A and B, which includes all elements that are in A but not in B.

Why is it important to understand the intersection of sets?

Understanding the intersection of sets is crucial for proving properties involving multiple sets and for determining how elements relate to each other across different contexts.

What happens if an element belongs to both A and B?

If an element belongs to both sets A and B, it means that the element is part of the intersection A ∩ B.

What does it mean if an element X is in B - A?

If an element X is in B - A, it indicates that X is part of set B but not part of set A, emphasizing that X cannot belong to A while being in B.

Can an intersection of sets result in an empty set?

Yes, the intersection of sets can result in an empty set if there are no common elements between the sets being considered.

How can one prove relationships involving set intersections?

To prove relationships involving set intersections, one can select elements and demonstrate how they belong to the respective sets and their intersections, applying logical reasoning to show the required properties.

What is the significance of the empty set in set theory?

The empty set is significant in set theory as it represents the absence of elements. It serves as a foundational concept, indicating that any intersection involving the empty set will also result in an empty set.

What resources does the lecturer recommend for further learning?

The lecturer recommends subscribing to their channel and engaging with additional videos on related topics, such as group theory and linear algebra, for a deeper understanding of mathematical concepts.