El gradiente de una función - concepto e interpretación
Summary
TLDR本视频介绍了标量场梯度的定义及其在二维和三维空间中的几何和物理意义。通过分析函数的梯度,阐明了梯度向量如何表示一个标量场在某点的变化速率,且该向量始终与等值线或等值面垂直。此外,还通过具体例子展示了梯度在函数图形中的表现,并强调梯度在物理学中的重要性,特别是它与场的变化和位置之间的关系。
Takeaways
- 😀 课题的主题是梯度的定义和物理意义,它是一个向量,表示一个标量场的变化率。
- 😀 梯度的物理解释是描述在某一点上标量场变化的方向和速度。
- 😀 梯度的公式是由函数的偏导数组成,描述了函数如何随独立变量(如x和y)变化。
- 😀 梯度的计算适用于二维和三维变量空间,具体公式会有所不同。
- 😀 函数必须是可微的,才能计算梯度,因为只有可微函数才有明确的变化方向和速率。
- 😀 梯度不仅是函数在特定点的特征,还可以扩展到整个定义域,形成一个梯度场。
- 😀 梯度是与等高线或等值曲线垂直的,表示标量场变化最大的方向。
- 😀 梯度在图形中的表示通常为矢量箭头,显示在二维平面上或三维空间中。
- 😀 在二维中,梯度表示在给定点的函数增长最快的方向,且与等高线正交。
- 😀 在三维空间中,梯度与曲面上的法线方向相同,表示该曲面变化最剧烈的方向。
- 😀 通过具体例子演示了梯度的计算过程,帮助更好地理解梯度的几何和物理意义。
Q & A
什么是梯度?
-梯度是一个向量,表示标量场在某一点的变化率。它的方向指示了标量场增长最快的方向,而其大小则表示变化的速率。
梯度的物理意义是什么?
-梯度在物理上描述了标量场如何随着位置的变化而变化。它告诉我们从某一点开始,标量场增加的最快方向。
梯度为什么与可微函数相关?
-梯度的定义要求函数是可微的。只有当函数是连续并且可以求导时,才可以定义梯度,因为梯度涉及到求取函数的偏导数。
在二维空间中,梯度的方向与曲线有什么关系?
-在二维空间中,梯度是与等高线(水平曲线)垂直的。也就是说,梯度指向的是标量场变化最陡峭的方向,而等高线代表了标量场值不变的地方。
梯度在三维空间中的定义是怎样的?
-在三维空间中,梯度是一个具有三个分量的向量,分别是函数对每个变量的偏导数。梯度向量垂直于函数的等高面(水平面)。
如何计算一个函数的梯度?
-计算一个函数的梯度时,我们首先需要求出该函数对每个独立变量的偏导数,然后将这些偏导数组合成一个向量,得到梯度向量。
梯度在图形中是如何表示的?
-在图形中,梯度通常通过向量表示。二维图中,梯度向量指向标量场变化最快的方向,而三维图中,梯度向量垂直于函数的等高面。
什么是梯度场?
-梯度场是由函数在其整个定义域上的梯度向量组成的场。它是一个向量场,每个点都有一个与该点相关联的梯度向量。
什么是水平曲线(等高线)?
-水平曲线(等高线)是函数值保持不变的曲线。在二维图形中,等高线表示所有函数值相同的位置,梯度向量与这些曲线垂直。
梯度向量与切平面有什么关系?
-在三维空间中,梯度向量与函数的切平面垂直。梯度指示了函数值变化最快的方向,而切平面表示在某点附近的线性近似。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

What does the second derivative actually do in math and physics?

Unlock Your Creativity with Visualization: The Power of Spatial Thinking
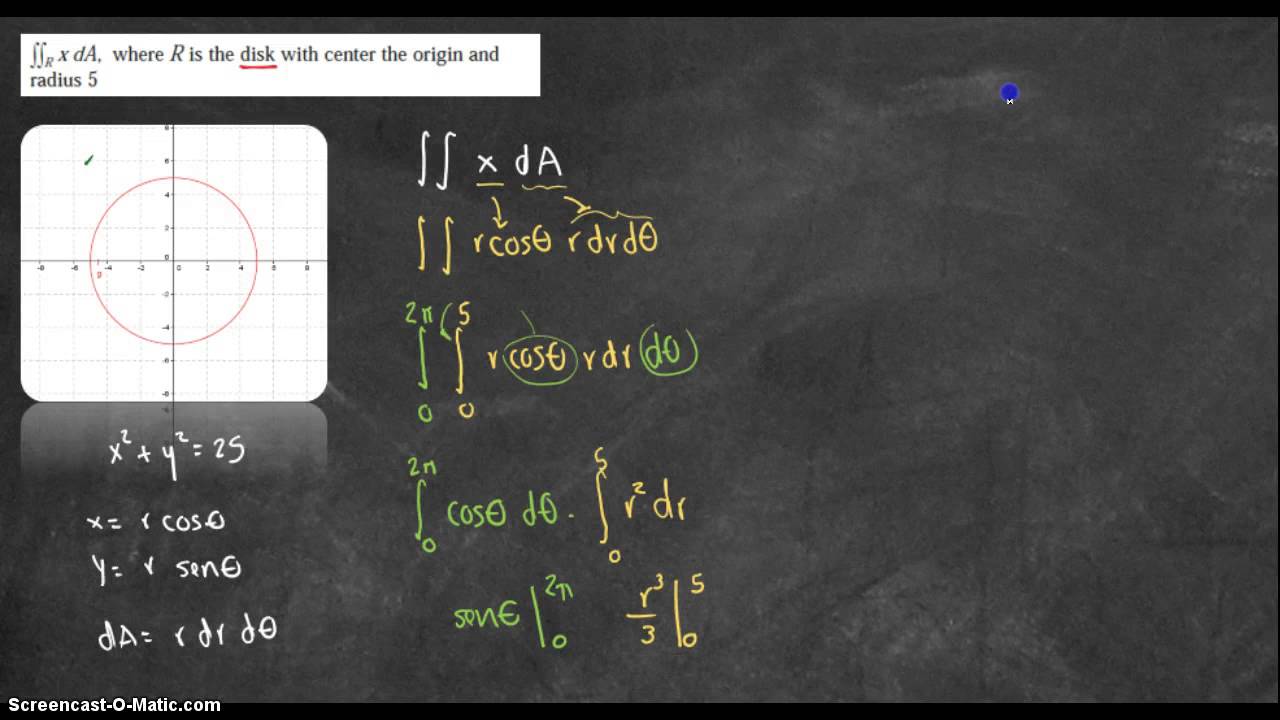
Ejemplo 01 - Ingtegrales polares

CCIR - Quantum Physics: Information, Foundations And Gravity - TA Session #1

Introduction to linear independence | Vectors and spaces | Linear Algebra | Khan Academy

Nutrition basics for healthy eating | Nutrition Time - EP15 | Lifesum

FRAMEWORK 16: an almost perfect Linux laptop
5.0 / 5 (0 votes)