Understanding the Area Moment of Inertia
Summary
TLDRThis video script explores the concept of area moment of inertia, crucial for understanding a structure's resistance to bending. It explains how material distribution in a cross-section affects stiffness, introduces the calculation of area moment of inertia through integration, and highlights the I-beam's efficiency. The script also covers the parallel axis theorem for calculating moments of inertia for non-centroidal axes and distinguishes between area and mass moments of inertia. Practical applications in beam and column analysis are discussed, including the use of flexural rigidity and the radius of gyration.
Takeaways
- 🌟 The stiffness of a plank of wood is greater when the load is applied to the shorter side of its rectangular cross-section.
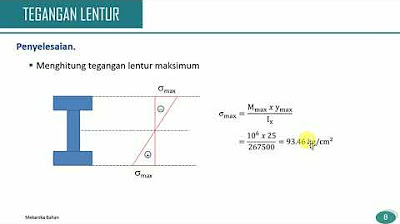
- 📏 The area moment of inertia (I) quantifies a cross-section's resistance to bending and is calculated based on how the area is distributed relative to a bending axis.
- 🏗️ I-beams are efficient at resisting bending because they position most of the material far from the bending axis.
- 📐 The area moment of inertia is not unique to a cross-section and varies depending on the axis of bending.
- 🧩 Area moment of inertia can be approximated by dividing a cross-section into small elements, each contributing to the total based on its area and distance from the axis.
- ✏️ The area moment of inertia is precisely defined using integration, with the result denoted by I and subscripted by the reference axis.
- 📘 Reference texts often provide area moment of inertia equations for centroidal axes, which pass through the centroid of the cross-section.
- 🔄 The parallel axis theorem allows calculating the area moment of inertia for any axis parallel to a centroidal axis by adding the moment of inertia of the centroidal axis to the product of the area and the square of the distance between the axes.
- 🔢 The area moment of inertia is crucial for analyzing beams and columns, appearing in equations that define deflection and critical buckling load.
- 🔄 The radius of gyration represents the distance at which the area of a cross-section can be condensed into a strip to maintain the same moment of inertia, and it is calculated based on the area moment of inertia.
- 🔄 The polar moment of inertia (J) represents the resistance to twisting and is calculated using a reference axis perpendicular to the cross-section plane.
Q & A
Why is it more efficient to apply load to the shorter side of a rectangular cross-section?
-Applying load to the shorter side of a rectangular cross-section is more efficient because it distributes the material closer to the bending axis, which increases the resistance to bending and makes the plank stiffer.
What is the area moment of inertia and why is it important?
-The area moment of inertia is a measure of a cross-section's resistance to bending, quantifying how the area is distributed relative to a particular axis. It's important in structural engineering as it helps to predict how materials will behave under bending loads.
How does the distance of material from the bending axis affect the stiffness of a cross-section?
-The further the material is spread from the bending axis, the stiffer the cross-section tends to be. This is because the moment of inertia increases with the square of the distance from the axis, enhancing the section's resistance to bending.
Why is the I-beam an efficient cross-section for construction?
-The I-beam is efficient because it locates the majority of the material as far as possible from the bending axis, which maximizes the area moment of inertia and thus the resistance to bending for a given amount of material.
How is the area moment of inertia calculated for an arbitrary cross-section?
-The area moment of inertia for an arbitrary cross-section can be calculated by integrating the quantity equal to the area of each small element (dA) multiplied by the square of its distance (Y^2) from the reference axis.
What is the unit of area moment of inertia and why is it always positive?
-The unit of area moment of inertia is length to the fourth power. It is always positive because it involves the square of distances, which are inherently non-negative.
How do you calculate the area moment of inertia for a rectangular cross-section?
-For a rectangular cross-section, the area moment of inertia (I-X) about the centroidal axis can be calculated using the integral of b*dy*(y^2) from -h/2 to h/2, resulting in I-X = b*h^3/12.
What is the parallel axis theorem and how is it used?
-The parallel axis theorem allows for the calculation of the area moment of inertia for any axis parallel to a known centroidal axis by summing the moment of inertia about the centroidal axis and the product of the cross-sectional area and the square of the distance between the axes.
Why is the area moment of inertia different for different axes?
-The area moment of inertia is not a unique property of a cross-section; it varies depending on the axis about which the bending is considered. Different axes will have different distances from the material's centroid, affecting the calculated moment of inertia.
How can the area moment of inertia be used to analyze beams and columns?
-The area moment of inertia is used in the analysis of beams and columns to calculate deflection, flexural rigidity, and critical buckling load. It represents the resistance due to the geometry of the beam cross-section to bending.
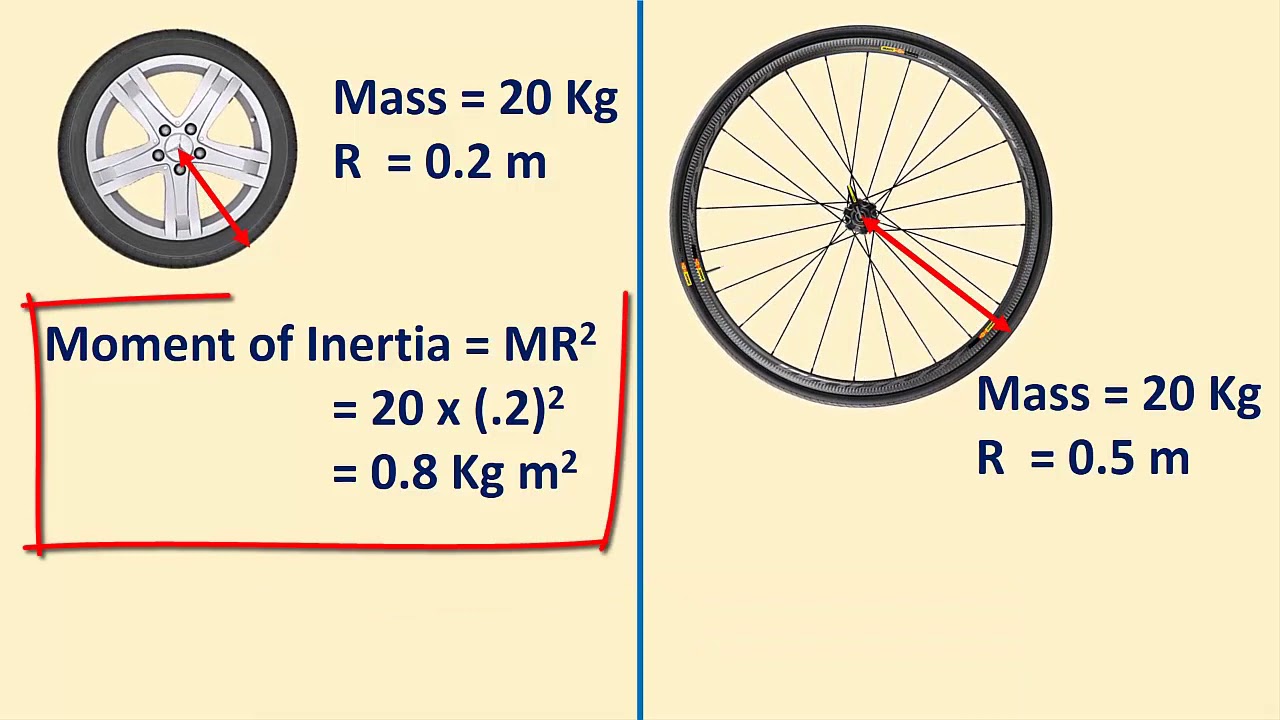
What is the difference between area moment of inertia and mass moment of inertia?
-Area moment of inertia is a geometric property that describes a shape's resistance to bending, while mass moment of inertia is a measure of an object's resistance to changes in rotational velocity. They have different units and uses.
What is the polar moment of inertia and how is it calculated?
-The polar moment of inertia (J) represents the resistance of a cross-section to twisting about a reference axis perpendicular to the plane of the cross-section. It is calculated using integration with the distance (Rho) to the axis, and can be found using the perpendicular axis theorem as J = I-X + I-Y.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)