Linear Regression, Clearly Explained!!!
Summary
TLDRThis educational video script from 'Static Quest' introduces linear regression, also known as general linear models, through a three-step process: fitting a line to data using least squares, calculating R-squared to measure the model's goodness of fit, and determining the statistical significance of R-squared with a p-value. The script uses the example of predicting mouse size from weight to explain these concepts, emphasizing the importance of both R-squared and p-value in assessing the reliability of the linear model.
Takeaways
- 📊 **Linear Regression Overview**: The script introduces linear regression, also known as general linear models, focusing on its application in understanding relationships within datasets.
- 🔍 **Least Squares Method**: It explains the use of least squares to fit a line to data, which involves minimizing the sum of the squares of the vertical distances from the data points to the line.
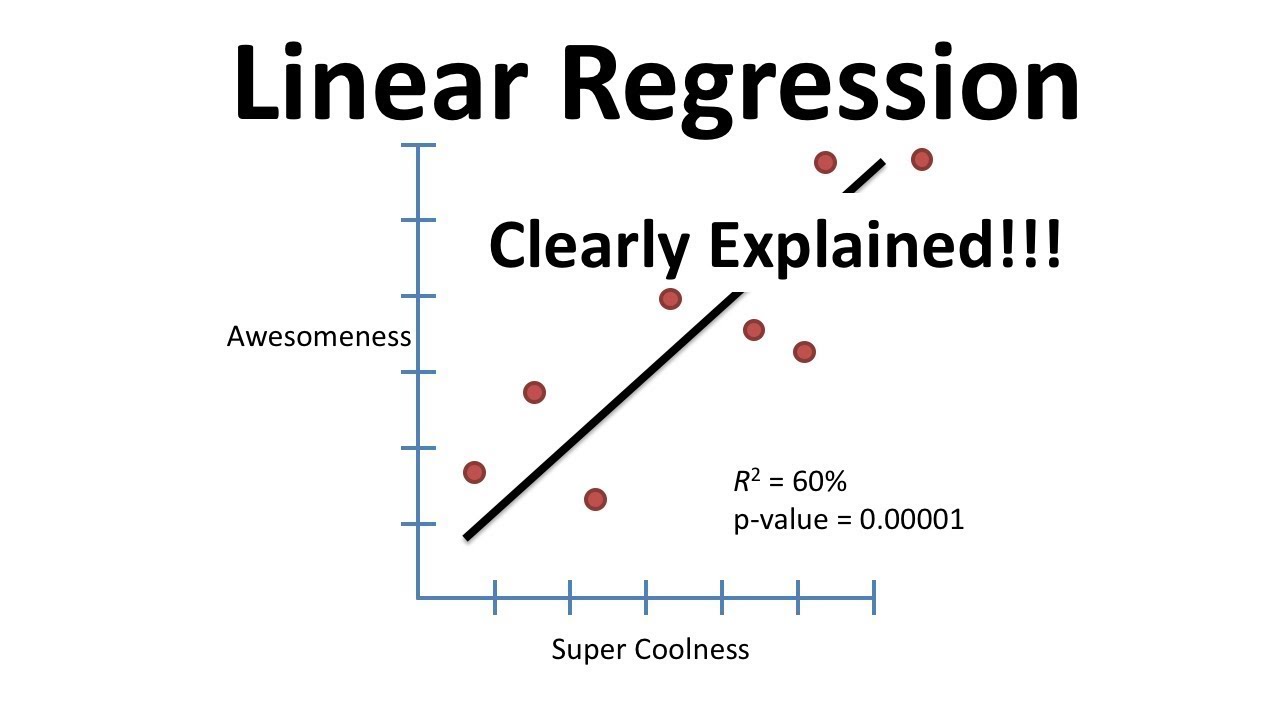
- 📐 **Calculating R-Squared**: The script details how to calculate R-squared, a statistical measure that represents the proportion of variance for a dependent variable that's explained by an independent variable or variables in a regression model.
- 🧮 **Residuals and Sum of Squares**: It discusses the concept of residuals (the difference between observed and predicted values) and how summing their squares is used in the fitting process.
- 📉 **Variance and Its Components**: The explanation includes the breakdown of total variance into explained (by the model) and unexplained variance, which is crucial for understanding the effectiveness of the model.
- 🔢 **Fitting a Line to Data**: The process of fitting a line to data involves rotating the line to minimize the sum of squared residuals, which is explained through the concept of least squares.
- 📈 **R-Squared in Detail**: The script provides a comprehensive review of R-squared, including its calculation and interpretation, emphasizing its role in measuring the goodness of fit of a model.
- 🔄 **Adjusting for Parameters**: It highlights the need for adjusted R-squared to account for the number of parameters in the model, which helps prevent overfitting and provides a more accurate measure of model fit.
- 📊 **Three-Dimensional Data Analysis**: The script extends the concept of linear regression to three dimensions, discussing how a plane can be fit to data points representing multiple variables.
- ⚖️ **Statistical Significance of R-Squared**: The importance of calculating a p-value for R-squared is emphasized to determine the statistical significance of the model's explanatory power.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is linear regression, also known as general linear models, with a focus on the concepts of least squares, R-squared, and p-values.
What does the term 'least squares' refer to in the context of linear regression?
-In the context of linear regression, 'least squares' refers to the method of fitting a line to a set of data by minimizing the sum of the squares of the vertical distances (residuals) between the data points and the line.
How is R-squared calculated and what does it represent?
-R-squared is calculated by taking the sum of squares around the mean, subtracting the sum of squares around the fit, and then dividing by the sum of squares around the mean. It represents the proportion of the variance in the dependent variable that is predictable from the independent variable(s).
What is the purpose of calculating a p-value for R-squared?
-The purpose of calculating a p-value for R-squared is to determine if the observed relationship between the variables, as quantified by R-squared, is statistically significant and not due to random chance.
What is the role of residuals in linear regression?
-Residuals in linear regression are the differences between the observed values and the values predicted by the regression model. They are used to assess the fit of the model and to calculate R-squared.
Why is it important to consider the number of parameters when calculating R-squared?
-It is important to consider the number of parameters when calculating R-squared because adding more parameters to a model can artificially inflate the R-squared value, making the model seem better than it actually is. Adjusting for the number of parameters helps to prevent overfitting.
What does the video script mean by 'adjusted R-squared'?
-The 'adjusted R-squared' is a modified version of R-squared that has been adjusted for the number of predictors in the model. It is used to compare models with different numbers of predictors while accounting for the potential overfitting that can occur with additional parameters.
How does the video script explain the concept of degrees of freedom in the context of linear regression?
-The video script explains degrees of freedom as the number of values in the final calculation of a statistic that are free to vary. In the context of linear regression, it is used to turn sums of squares into variances, which is crucial for calculating the F-statistic and the p-value.
What is the significance of the F-distribution in calculating the p-value for R-squared?
-The F-distribution is used to calculate the p-value for R-squared because it provides a way to compare the observed F-statistic against a theoretical distribution of F-statistics that would be expected under the null hypothesis. This comparison helps determine if the observed relationship is statistically significant.
Why is it necessary to generate random data sets to calculate the p-value for R-squared?
-Generating random data sets is necessary to create a distribution against which the observed F-statistic can be compared. This process helps to determine how extreme the observed F-statistic is relative to what would be expected by chance alone, thus providing the p-value.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)