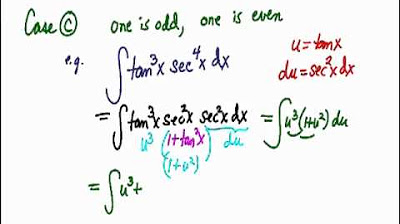Section 6.2 - Trig integrals and substitution - Part 2
Summary
TLDRThis educational video script focuses on integral calculus, specifically integrals involving powers of tangent and secant functions. It outlines strategies for solving integrals when the power of tangent is odd or the power of secant is even, and when both conditions are met simultaneously. The script provides step-by-step examples, demonstrating how to simplify integral expressions using trigonometric identities and substitution methods. It emphasizes the importance of recognizing when the power of tangent is odd, which allows for the use of specific identities to simplify the integral. The tutorial is designed to help viewers understand and tackle complex integrals in calculus.
Takeaways
- 📚 The video discusses strategies for integrating functions involving powers of tangent and secant.
- 🔑 There are two straightforward cases: when the power of tangent is odd or the power of secant is even.
- ❌ If the power of tangent is even and the power of secant is odd, a generic strategy doesn't exist, and a case-by-case approach is needed.
- 🤔 The strategy involves pulling out one tangent or secant from the integral to simplify the expression.
- 🆚 For an odd power of tangent, after pulling out one tangent, the remaining power is even, allowing the use of a specific trigonometric identity.
- 🆓 The identity used is tangent squared equals secant squared minus one, which helps rewrite the integral in terms of secant.
- 🔄 A u-substitution is performed where u is secant, and du is secant tangent, simplifying the integration process.
- 📉 The integral is then integrated with respect to u, and the results are replaced back in terms of the original variable.
- 🔠 For an even power of secant, the strategy is to pull out secant squared and use the identity secant squared equals tangent squared plus one.
- 🔢 The final answer is expressed in terms of the original variable, with the integrated result adjusted for the pulled-out secant or tangent.
Q & A
What are the two cases where it is easy to solve integrals involving powers of tangent and secant?
-It is easy to solve when the power of tangent is odd or the power of secant is even. If both conditions are met, either method can be used to find the correct answer.
Why is it helpful when the power of tangent is odd in solving integrals?
-When the power of tangent is odd, you can pull out one tangent and then use trigonometric identities to simplify the remaining even power of tangent, making it easier to solve.
What is the first step when dealing with an integral where the power of tangent is odd?
-The first step is to pull out one tangent and one secant from the integral. This allows you to work with an even power of tangent, which can be simplified using a trigonometric identity.
What trigonometric identity is used to simplify the integral after pulling out one tangent and secant?
-The identity used is tangent^2(x) = secant^2(x) - 1, which allows you to rewrite the remaining even power of tangent in terms of secant.
Why is a substitution method used in these integrals, and what is the common substitution?
-A substitution method is used to simplify the integral into a form that is easier to integrate. The common substitution is u = secant(x), where the derivative of secant is secant(x) * tangent(x), helping to reduce the complexity.
How do you rewrite the integral after the substitution u = secant(x)?
-After substitution, the integral becomes a polynomial in terms of u, which can be expanded and integrated using basic rules of integration.
What happens if the power of tangent is even and the power of secant is odd?
-If the power of tangent is even and the power of secant is odd, the integral becomes more difficult, and no generic strategy can be applied. Each case must be handled individually.
What is the strategy when the power of secant is even?
-When the power of secant is even, the strategy is to pull out a factor of secant^2 and then use the identity secant^2(x) = 1 + tangent^2(x) to express the integral in terms of tangent.
How do you handle an integral where both tangent and secant have powers greater than 2?
-In such cases, you first pull out secant^2 and use the identity secant^2(x) = 1 + tangent^2(x) to rewrite everything in terms of tangent, then proceed with substitution.
What is the final form of the integral after solving for an odd power of tangent and an even power of secant?
-The final form of the integral is a polynomial in secant(x), which can be integrated and expressed in terms of secant(x) to a power, plus a constant (C).
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
5.0 / 5 (0 votes)