Solving One and Two-Step Inequalities
Summary
TLDRThis video tutorial guides viewers through solving one and two-step inequalities, emphasizing the process is akin to solving equations but with an additional rule: flipping the inequality sign when multiplying or dividing by a negative number. The instructor uses step-by-step examples to illustrate the method, including isolating variables and balancing equations, and introduces a graphing technique to visually represent solutions. The lesson concludes with practice problems and an interactive call-to-action for viewers to apply the concepts.
Takeaways
- 📚 Start by reviewing the process of solving equations as it is similar to solving inequalities.
- 📝 When solving equations or inequalities, always aim to isolate the variable by using inverse operations.
- ⚖️ Maintain balance in the equation or inequality by performing the same operation on both sides.
- 🔄 Use PEMDAS in reverse order to solve equations and inequalities: start with addition/subtraction, then move to multiplication/division.
- 🔄 Remember that when you multiply or divide by a negative number in an inequality, you must flip the inequality sign.
- 📉 For one-step inequalities, isolate the variable using inverse operations and ensure the inequality symbol remains balanced.
- 📈 Graph inequalities by using a number line, with a closed circle for 'less than or equal to' and an open circle for 'greater than'.
- 🔍 Check your work by plugging a number from the shaded area back into the original inequality to ensure it holds true.
- 🔢 In two-step inequalities, follow the same process as one-step but with additional operations to isolate the variable.
- 📌 Keep in mind that the process of solving inequalities is the same as solving equations, with the additional rule for handling negatives.
- 💡 The ultimate goal is to isolate the variable and ensure the inequality sign is correctly oriented when graphing or checking your solution.
Q & A
What is the main topic of the video?
-The main topic of the video is teaching how to solve one and two-step inequalities.
What is the process for solving equations similar to solving inequalities?
-The process for solving equations is similar to solving inequalities because both involve using inverse operations to isolate the variable and maintaining balance on both sides of the equation or inequality.
What is the goal when solving an inequality?
-The goal when solving an inequality is to isolate the variable, getting it by itself on one side of the inequality.
What is an important rule to remember when dealing with inequalities?
-An important rule to remember when dealing with inequalities is that when you multiply or divide by a negative number, the inequality sign must be flipped.
How do you check if an inequality has been solved correctly?
-You can check if an inequality has been solved correctly by plugging in a number from the shaded area on the graph into the original inequality and the simplified inequality to see if it holds true.
What is the difference between solving an equation and an inequality when it comes to graphing?
-When graphing, the difference between solving an equation and an inequality is that for equations, you use a solid dot to indicate the exact solution, while for inequalities, you use a closed or open circle depending on whether the inequality includes an 'equal to' or not.
What is the first step the instructor takes when solving an inequality?
-The first step the instructor takes when solving an inequality is to draw a line on the inequality symbol to separate the two sides and ensure the inequality remains balanced.
What is the significance of the number '5.5' in the script?
-The number '5.5' is used as an example in the script to illustrate how to handle division by a negative number in an inequality and the subsequent flipping of the inequality sign.
How does the process of solving a two-step inequality differ from a one-step inequality?
-The process of solving a two-step inequality is similar to a one-step inequality, but it involves more operations such as both addition/subtraction and multiplication/division, with the additional rule of flipping the inequality sign when multiplying or dividing by a negative number.
What is the purpose of the final practice problems in the video?
-The purpose of the final practice problems in the video is to allow viewers to apply the concepts learned about solving inequalities and to test their understanding through practical application.
What is the role of PEMDAS in solving equations and inequalities?
-PEMDAS (Parentheses, Exponents, Multiply or Divide, Add or Subtract) is a guideline for the order of operations in mathematics. When solving equations and inequalities, the process often involves doing the opposite of these operations in reverse order to isolate the variable.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

How to Solve One-Step Inequalities | Math with Mr. J

Why Do We Flip the (Inequality) Sign When Dividing by a Negative?
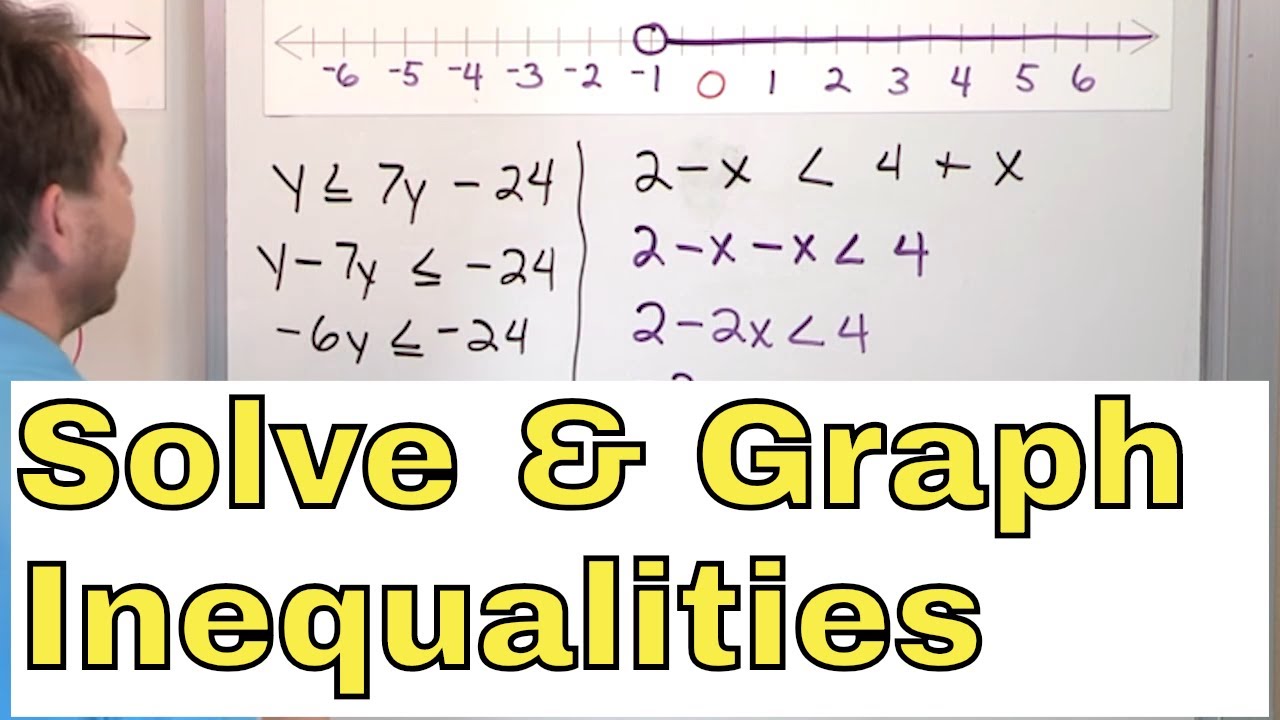
12 - Solving & Graphing Inequalities w/ One Variable in Algebra, Part 1

KALKULUS | Sistem Bilangan Real - Part 4 | Pertidaksamaan

8TH EDITION | BOOK 2 | EXERCISE 3A | QUESTION # 1, 2, 3

Rational Inequalities
5.0 / 5 (0 votes)
