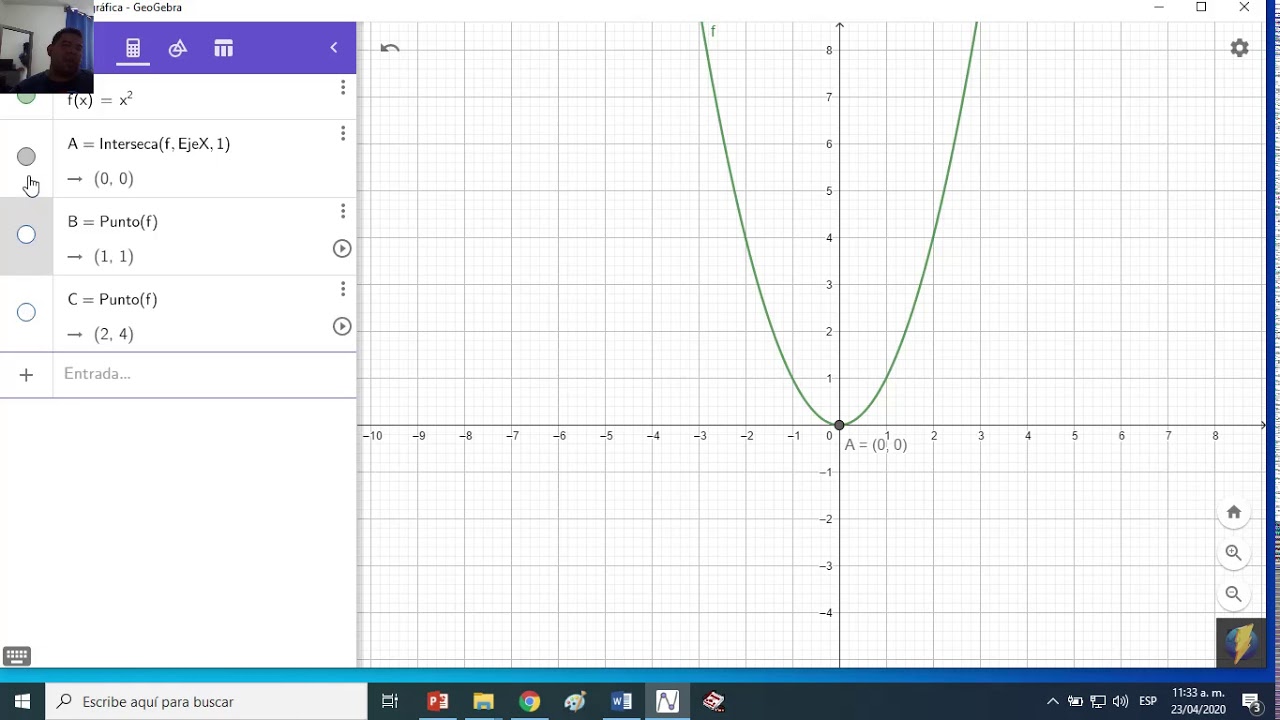
¿Cómo graficar funciones?

Summary

En este video de Academia Internet, se enseña cómo graficar funciones matemáticas comunes. Se explican las características de las funciones cuadráticas, valor absoluto y racionales, y cómo identificar su vértice para dibujar la gráfica. Se practican técnicas para encontrar el dominio y rango de cada función, y se destacan las similitudes y diferencias entre ellas para una mejor comprensión.

Takeaways

• 📚 Aprender a graficar funciones es el objetivo del video, destacando la función raíz cuadrada como ejemplo principal.
• 📈 Se mencionan diferentes tipos de funciones: cuadráticas, valor absoluto y racionales, cada una con sus características particulares.
• 📌 El valor absoluto y la función cuadrática pueden variar dependiendo de los signos en su expresión, lo cual es importante para su gráfica.
• 📍 La función raíz cuadrada tiene varias formas de representarse gráficamente, dependiendo de factores como los signos.
• 🔍 Las asíntotas son una característica importante en las funciones racionales, y se representan como líneas que podrían ser ejes si se prolongaran.
• 📐 El vértice es un punto clave en las funciones cuadráticas, y se encuentra igualando la expresión a cero.
• 📊 Conocer el vértice es fundamental para entender la forma de la gráfica de una función cuadrática.
• 📉 El dominio y el rango de una función son conceptos clave, y se pueden determinar a partir de su gráfica y su expresión matemática.
• 👀 La gráfica de la función valor absoluto y la función raíz cuadrada se describen con un punto de partida común, el vértice.
• 📋 Se resalta la importancia de no solo encontrar diferencias, sino también similitudes entre las funciones para una mejor comprensión.
• 👋 El video termina con un mensaje de despedida y cuidado, invitando a la audiencia a revisar el material de nuevo para una mejor comprensión.

Q & A

¿Qué tipo de funciones se discuten en el video?

El video trata sobre cómo graficar las funciones principales, incluyendo la función cuadrática, la función valor absoluto y la función racional.

¿Qué es un vértice en el contexto de las funciones?

Un vértice es el punto de cambio de inclinación en la gráfica de una función, generalmente se encuentra al igualar a cero el término de la función que contiene 'x'.

¿Cómo se encuentra el vértice de una función cuadrática?

Para encontrar el vértice de una función cuadrática, se iguala a cero el término que contiene 'x', y se resuelve para encontrar el valor de 'x'. Luego, se sustituye ese valor en la función para encontrar el valor de 'y' correspondiente.

¿Qué son las asíntotas y cómo se relacionan con la función racional?

Las asíntotas son líneas que la gráfica de una función racional se acerca pero nunca toca. Se llaman asíntotas porque 'no se tocan' (a-sin-tomas). Aparecen cuando hay denominadores en la función que se anulan, creando un límite vertical o horizontal en la gráfica.

¿Cómo se determina el dominio de una función?

El dominio de una función es el conjunto de todos los valores de 'x' para los que la función está definida. Se determina observando restricciones como raíces en el denominador o expresiones que podrían causar divisiones por cero.

¿Cómo se determina el rango de una función?

El rango de una función es el conjunto de todos los valores de 'y' que toma la función. Se determina a partir de la gráfica de la función, identificando los valores mínimos y máximos que puede alcanzar, así como cualquier restricción en el valor de 'y'.

¿Por qué es importante conocer las particularidades de cada función para graficarlas?

Conocer las particularidades de cada función es importante para entender su comportamiento, encontrar puntos clave como el vértice, y graficarlas correctamente, lo que facilita la comprensión y la predicción de su comportamiento en diferentes intervalos.

¿Qué es un esbozo de gráfica y cómo se realiza?

Un esbozo de gráfica es una representación aproximada de cómo se verá la gráfica de una función. Se realiza identificando puntos clave como el vértice, las asíntotas y los valores de dominio y rango, y luego trazando la curva a mano alzada.

¿Cómo se grafica la función valor absoluto y qué aspecto tiene?

La función valor absoluto se grafica identificando el punto de cambio de inclinación, que es donde el valor dentro del valor absoluto cambia de signo. La gráfica tiene una forma de V invertido, con una curva que se bifurca en el eje 'x'.

¿Cuál es la diferencia entre las gráficas de una función cuadrática y una función raíz cuadrada?

La gráfica de una función cuadrática tiene una forma de V, ya sea ascendente o descendente, mientras que la gráfica de una función raíz cuadrada tiene una forma de rampa que comienza en el eje 'x' y se eleva垂直mente.

¿Cómo se relacionan las diferencias y similitudes entre las funciones para una mejor comprensión?

Las diferencias y similitudes entre las funciones son importantes para entender su comportamiento y características. Conocer tanto las diferencias como las similitudes ayuda a establecer una comprensión más profunda y a prever cómo se comportarán en diferentes situaciones.