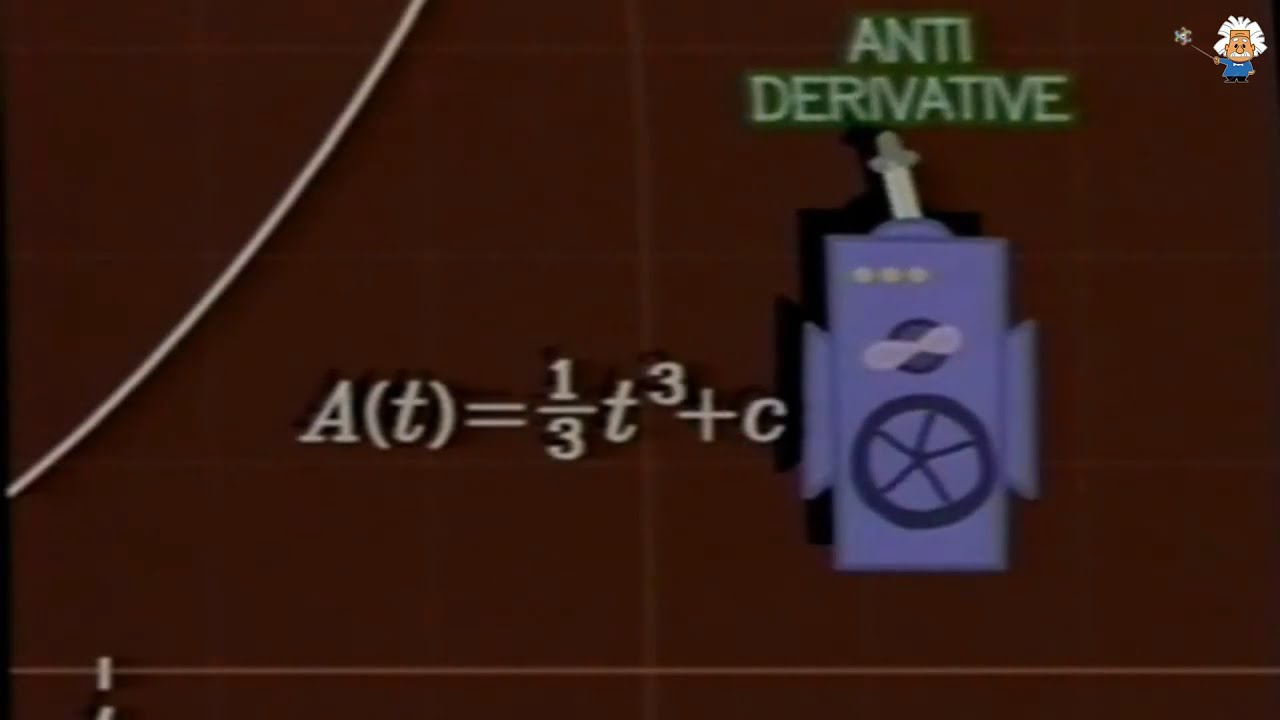History of Calculus - Animated

Summary

This script explores the rich history of calculus, tracing its roots from ancient Babylonia's sexagesimal system to the foundational works of Newton and Leibniz. It highlights the contributions of various civilizations, including the Greeks with Eudoxus and Archimedes, and Indian mathematicians like Bhaskaracharya and Madhava. The narrative underscores that calculus evolved over centuries, with different cultures developing similar concepts independently. The script also touches on the modern applications of calculus in fields like AI and machine learning, emphasizing its enduring significance.

Takeaways

• 📚 Calculus is the mathematical study of change, involving differential calculus for rates of change and integral calculus for quantities like areas and volumes.
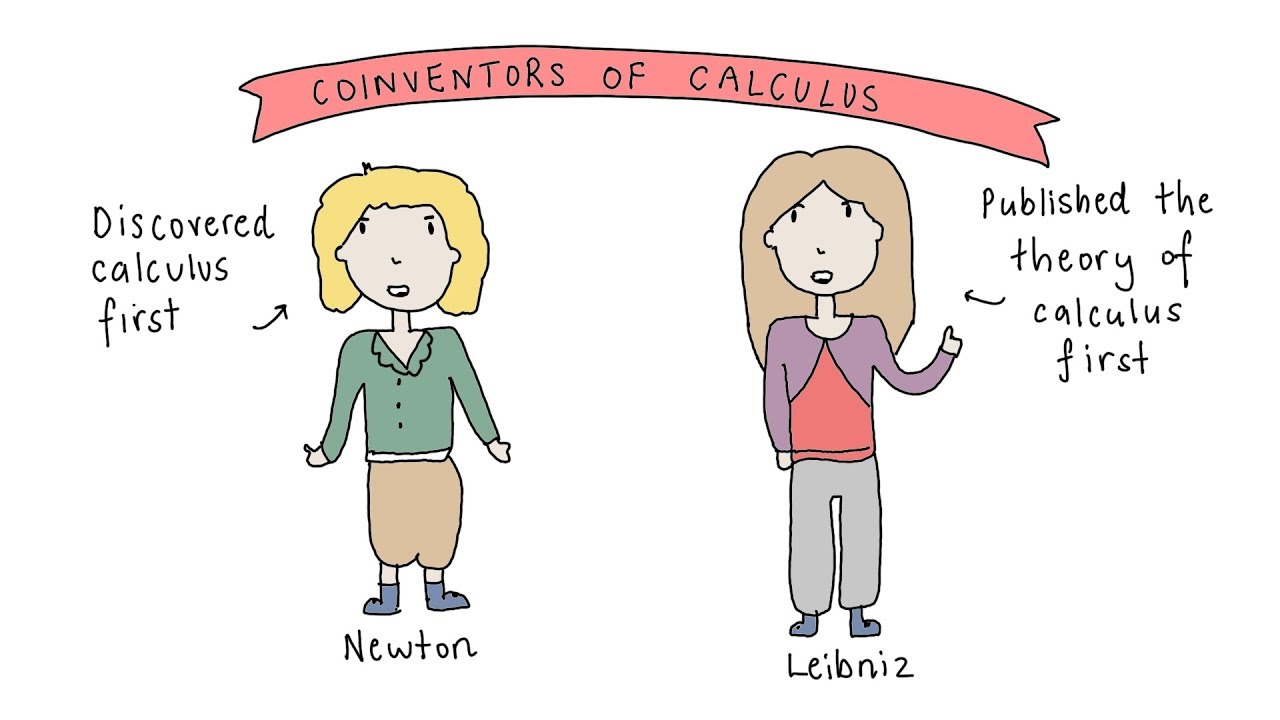
• 🕵️‍♂️ Isaac Newton and Gottfried Leibniz are credited with the foundational work on calculus, with Newton focusing on motion and Leibniz on infinitesimal distances.
• 🏛 Ancient civilizations like the Babylonians had early intuitions on infinite processes, using their sexagesimal number system for precise calculations.
• 📜 Babylonians recorded mathematical findings on clay tablets, known as cuneiforms, which included early geometric insights similar to integral calculus.
• 🌌 In 300 BC, Babylonian astronomers used geometry to study planetary motion, particularly Jupiter, and recorded velocities at instantaneous times.
• 🏛 Ancient Greek mathematicians like Eudoxus and Archimedes used the method of exhaustion to calculate areas of shapes, introducing the concept of limits.
• 📚 The method of exhaustion was particularly applied to circles, where the area was approximated by inscribing polygons with an increasing number of sides.
• 📖 In the 12th century, Indian mathematician Bhaskaracharya used calculus in his astronomical texts, predating Newton and Leibniz by centuries.
• 🔍 Madhava of 14th century India linked infinite series with geometry and trigonometry, formulating series expansions for sine, cosine, arctan, and pi.
• 🌐 The history of calculus is not straightforward, with contributions from various cultures and periods, and it continues to evolve and impact fields like machine learning and AI.
• 🌟 The script emphasizes that the development of calculus was a collective effort, with Newton and Leibniz synthesizing and formalizing the work of many predecessors.

Q & A

What is calculus and why is it significant in mathematics?

Calculus is the mathematical study of change, encompassing differential calculus, which deals with rates of change and slope, and integral calculus, which determines quantities like areas and volumes under changing conditions. It is significant as it is foundational to many fields, including physics, engineering, and economics.

Who are the two individuals most famously associated with the development of calculus?

Isaac Newton and Gottfried Wilhelm Leibniz are the two individuals most famously associated with the development of calculus. They are credited with independently laying the foundations of the subject as we know it today.

What is the historical significance of the sexagesimal number system used by the Babylonians?

The sexagesimal number system, with a base of 60, allowed the Babylonians to represent all real numbers using sixty symbols. This system enabled them to determine the square root of a rational number to any number of decimal places and contributed to their early intuition on the infinite process.

How did the Babylonians record their mathematical findings?

The Babylonians recorded their mathematical findings on clay tablets called cuneiforms, which provided a durable medium for their research and observations.

What was the connection between the Babylonian astronomers and the study of planetary motion?

Babylonian astronomers believed that the motion of planets was connected to various worldly phenomena. They used geometry to study the motion of planets, particularly Jupiter, recording velocities at instantaneous times to determine the distance traveled in a given interval.

Who were Eudoxus of Cnidus and Archimedes, and what was their contribution to the field of mathematics?

Eudoxus of Cnidus and Archimedes were prominent figures from ancient Greece who contributed to the field of mathematics by proving areas of shapes through the method of exhaustion, which involved inscribing polygons within circles and gradually increasing the number of sides to approximate the area of the circle.

What is the method of exhaustion, and how does it relate to the concept of limits in calculus?

The method of exhaustion is a technique used to find the area of shapes, particularly circles, by inscribing polygons with an increasing number of sides. As the number of sides approaches infinity, the area of the polygon approximates the area of the circle. This method introduced the concept of limits, which is fundamental to calculus.

What contributions did the Indian mathematician and astronomer Bhaskaracharya make to the field of calculus?

Bhaskaracharya, in the 12th century, wrote the Siddhanta Shiromani, which contained texts in astronomy with proofs using calculus. He proved concepts that were attributed to later mathematicians, such as the instantaneous speed of a planet being zero.

Who was Madhava, and what was his significant contribution to mathematics?

Madhava was a 14th-century Indian mathematician and astronomer who linked the idea of infinite series with geometry and trigonometry. He formulated infinite series expansions for sine, cosine, arctan, and even pi, which are now known as power series expansions.

Why is the credit for the discovery of certain mathematical concepts often attributed to Western mathematicians rather than their earlier Indian counterparts?

The credit for certain mathematical concepts is often attributed to Western mathematicians because their work was more widely disseminated and recognized in the historical academic circles. The original works of Indian mathematicians like Madhava were not as well-documented or accessible, leading to a delayed recognition of their contributions.

How did Newton and Leibniz differ in their approaches to calculus, and what are the implications of these differences?

Newton conceived his ideas in the context of motion, calling his calculus the method of fluxions, while Leibniz had a more mathematical interpretation, focusing on sums of infinitesimal distances. This difference in approach led to the notation used today in calculus, which is largely from Leibniz, despite Newton's earlier conception of the ideas.

What is the current relevance of calculus in modern fields such as machine learning and AI?

Calculus continues to be relevant in modern fields like machine learning and AI because it provides the mathematical tools necessary for understanding and modeling change and optimization. Concepts from calculus are used in algorithms and models to analyze data and make predictions.