GCSE Maths - How to Write Expressions for the nth term of Arithmetic Sequences #55
Summary
TLDRThis video tutorial teaches how to formulate an expression for the nth term of an arithmetic sequence, which is a sequence of numbers with a constant difference between consecutive terms. It demonstrates the process using an example sequence, explaining how to derive the expression by identifying the common difference and adjusting for the initial term. The video also provides a method to verify the correctness of the expression by applying it to a known term in the sequence, ensuring a clear understanding of the concept.
Takeaways
- 🔢 Arithmetic sequences involve a series of numbers where a constant value is added or subtracted successively.
- 📈 The nth term of an arithmetic sequence can be expressed using an algebraic formula, which simplifies finding any term in the sequence.
- 📝 An example formula for an arithmetic sequence is 'an = a1 + (n - 1) * d', where 'a1' is the first term, 'd' is the common difference, and 'n' is the term number.
- 🔍 To find the nth term, substitute the value of 'n' into the formula, allowing for quick calculation without manually adding the common difference each time.
- 📑 The script provides a step-by-step method to derive the formula for an arithmetic sequence by identifying the common difference and adjusting for the first term.
- 📉 For sequences that decrease, the common difference is negative, and the formula is adjusted accordingly, starting with '-d * n'.
- 🔄 The process of finding the formula involves considering an 'imaginary' term before the first term to determine what should be added or subtracted in the formula.
- 📌 The script demonstrates how to apply the formula to find specific terms in the sequence, such as the 3rd and 50th terms, using substitution.
- 📝 The script also illustrates how to derive the formula for sequences with different common differences, including negative and decimal values.
- 🔄 A verification method is suggested to ensure the accuracy of the derived formula by testing it against a known term in the sequence.
- 🤓 The video encourages sharing the knowledge with others and provides a comprehensive guide on understanding and working with arithmetic sequences.
Q & A
What is an arithmetic sequence?
-An arithmetic sequence is a series of numbers in which the same value is added or subtracted to get from one term to the next.
How is the arithmetic sequence in the video defined?
-The arithmetic sequence in the video is defined by the sequence 5, 9, 13, 17, and 21, which increases by 4 with each term.
What is the expression used to represent the nth term of the given arithmetic sequence?
-The expression used to represent the nth term of the given arithmetic sequence is 4n + 1.
What is the benefit of using an expression to represent an arithmetic sequence?
-The benefit of using an expression is that it allows us to find any term in the sequence without having to manually add the common difference to each previous term.
What is the first term in the arithmetic sequence shown in the video?
-The first term in the arithmetic sequence shown in the video is 5.
How do you find the third term of the sequence using the expression?
-To find the third term, you substitute n with 3 in the expression (4n + 1), which gives 4*3 + 1, resulting in 13.
How can you find a term in a large arithmetic sequence without manually adding the common difference?
-You can find a term in a large arithmetic sequence by plugging the term's position (n) into the expression representing the sequence.
What is the common difference in the arithmetic sequence used in the video?
-The common difference in the arithmetic sequence used in the video is 4.
How do you determine the expression for an arithmetic sequence?
-To determine the expression for an arithmetic sequence, you first find the common difference, then use it to form the expression starting with the common difference times n, and adjust for the first term if necessary.
What is the expression for the arithmetic sequence with a common difference of -5?
-The expression for the arithmetic sequence with a common difference of -5 is -5n + 31.
How do you verify if an expression for an arithmetic sequence is correct?
-You can verify if an expression is correct by using it to calculate a term in the sequence that you already know and comparing the result to the actual term.
What is the expression for the arithmetic sequence with a common difference of 1.5?
-The expression for the arithmetic sequence with a common difference of 1.5 is 1.5n - 0.5.
How does the video suggest checking the correctness of an arithmetic sequence expression?
-The video suggests checking the correctness of an arithmetic sequence expression by using it to calculate a known term and verifying if the result matches the actual term.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Harmonic Sequence (Tagalog/Filipino Math)

Barisan dan Deret Aritmatika Kelas 10 Kurikulum Merdeka

Finding the Arithmetic Means - Arithmetic Sequence Grade 10 Math

Pola bilangan - part 2
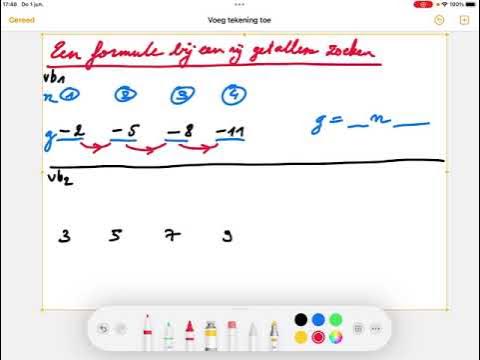
Een formule voor een rij getallen zoeken

ARITHMETIC SEQUENCE AND NTH TERM OF ARITHMETIC SEQUENCE || GRADE 10 MATHEMATICS Q1
5.0 / 5 (0 votes)