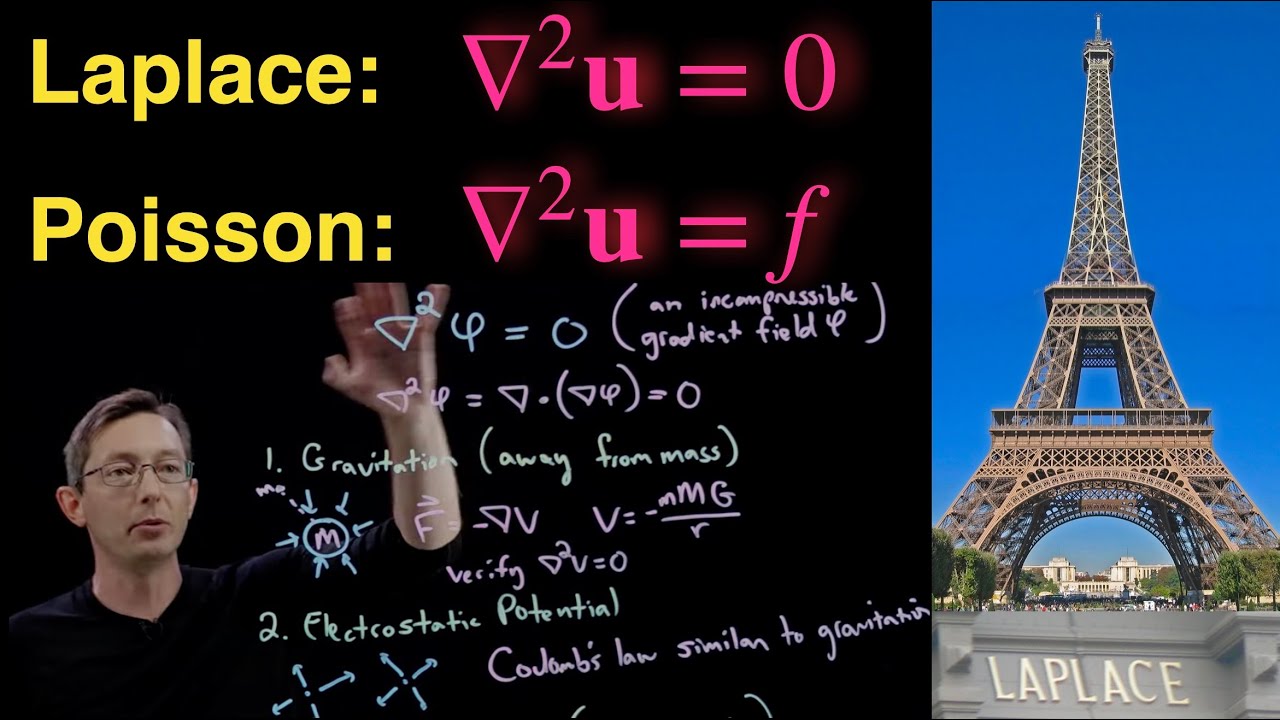This is why you're learning differential equations

Summary

This video explores the importance of differential equations in understanding natural phenomena and real-world applications. It delves into how these equations model population growth, fluid dynamics, electromagnetism, and even the motion of orbiting bodies. The script uses examples from TV shows, gym exercises with chains, and the spread of the coronavirus to illustrate how differential equations describe complex systems. The video encourages viewers to learn more about these foundational mathematical tools through Brilliant's courses, which focus on practical applications.

Takeaways

• 📚 We learn differential equations because they describe how nature and the universe work, often appearing in complex systems like population growth, fluid dynamics, and electromagnetism.
• 🔍 Differential equations can be challenging to solve, but they provide valuable insights into various phenomena, such as modeling population growth or the movement of fluids.
• 🌐 Maxwell's equations, which are four fundamental differential equations, are crucial for understanding electromagnetism, the basis for technologies like phones, radio, Wi-Fi, and GPS.
• 🔑 Differential equations can be interpreted to find specific solutions, such as the unique curve that has an area under it twice the numerical value of its arc length over any interval.
• 📈 The script uses the TV show 'Numbers' to illustrate how differential equations can model real-world scenarios, such as the pursuit curve used by the FBI to predict criminal movements.
• 🚀 Pursuit curves are used in various contexts, including missile guidance systems and aircraft navigation, and are derived from differential equations considering the motion and direction of chasing and chased objects.
• 🏋️‍♂️ The video discusses the complex dynamics of exercising with chains, which involves a second-order nonlinear differential equation due to the changing mass as the chain is lifted.
• 🦠 The spread of infectious diseases like COVID-19 can be modeled using differential equations, which consider the rates of change in susceptible, infected, and recovered populations.
• 🌱 Population growth models, such as the SI model for infections, are simplified differential equations that help predict how diseases spread and can be controlled through various interventions.
• 🤖 The script highlights the importance of understanding the stories and meanings behind differential equations, which can be applied to a wide range of fields, from physics to biology and epidemiology.
• 🎓 Brilliant.org offers courses on differential equations that focus on real-world applications, providing a comprehensive learning experience for students and enthusiasts alike.

Q & A

What is the primary reason for learning differential equations according to the video?

Differential equations describe how nature works and are fundamental in modeling various real-world phenomena, such as population growth, fluid movement, and electromagnetism.

Can differential equations always be solved exactly?

No, differential equations are often tough and sometimes impossible to solve exactly, but they can still provide valuable insights into the phenomena they model.

What are Maxwell's equations, and why are they important?

Maxwell's equations are a set of four differential equations that describe electromagnetism, which is fundamental to how phones, radio, Wi-Fi, and GPS work.

How do differential equations relate to the motion of objects in physical contact or in orbit?

Differential equations describe the motion of objects when a force is exerted, whether through physical contact or gravitational force, as seen in orbiting bodies.

What is a pursuit curve, and how is it used in real-world scenarios?

A pursuit curve is the path traced by one object chasing another. It can be applied in scenarios such as a cheetah chasing a gazelle or in missile guidance systems, aircraft, and submarines.

How do chains in gym equipment illustrate the complexity of differential equations?

Chains in gym equipment add weight as the bar moves up, creating a scenario where the mass changes with height. This requires a second-order nonlinear differential equation to describe the motion.

What does the SI model represent in epidemiology?

The SI (Susceptible-Infected) model represents the transition of individuals from susceptible to infected in a population, helping to predict the spread of infectious diseases.

How can differential equations model the spread of a virus like COVID-19?

Differential equations can model the spread of a virus by describing the rate of change of susceptible, infected, and recovered individuals in a population over time, as seen in the SIR model.

What is the significance of population growth models in differential equations?

Population growth models use differential equations to describe how a population grows at a rate proportional to its current value, incorporating factors like birth, death, and interactions between species.

How does the video illustrate the real-world application of differential equations in engineering and physics?

The video discusses various real-world applications, including modeling the motion of rockets with changing mass, the spread of diseases, and the behavior of systems like beams and waves, showing the practical importance of differential equations in engineering and physics.

Outlines

00:00

📚 Introduction to Differential Equations

This paragraph introduces the importance of differential equations in understanding the workings of nature and the universe. It highlights their applications in various fields such as population growth modeling, fluid dynamics, electromagnetism (Maxwell's equations), and forces in orbiting bodies. The paragraph also touches on the narrative aspect of equations, using an example that relates to the area under a curve and its arc length, leading to the derivation of a specific differential equation. The discussion emphasizes the real-world significance of these mathematical tools, setting the stage for further exploration in the video.

05:01

🔍 Pursuit Curves in Real-World Scenarios

This section delves into the concept of pursuit curves, using a TV show scenario where the FBI tracks criminals' movements to predict their next actions. It explains how differential equations can model the path of a pursuing object, assuming a known path for the target and the pursuer's constant direction towards the target. The paragraph outlines the mathematical process of deriving a pursuit curve, involving vector representation, normalization, and the use of dot products. It also discusses variations of pursuit curves and their applications in missile guidance systems, aircraft, and submarines, showcasing the practicality of differential equations in various contexts.

10:04

🏋️‍♂️ The Physics of Chain-Loaded Exercises

This paragraph explores the complex physics involved in exercises using chains, such as bench presses or squats, where the weight increases as the barbell is lifted. It explains how the changing mass of the lifted chain segment affects the equation of motion, leading to a second-order nonlinear differential equation. The discussion simplifies the scenario by assuming a barbell with no mass and a constant lifting force, highlighting the need to consider changing mass in the analysis. The paragraph emphasizes the broader implications of analyzing systems with variable mass, such as rocket propulsion, where mass changes due to fuel consumption.

15:04

🌡 Modeling the Spread of Infectious Diseases

This section discusses the application of differential equations in modeling the spread of infectious diseases, using the coronavirus pandemic as a case study. It introduces the basic SIR (Susceptible, Infected, Recovered) model, which describes the dynamics of disease spread through a population. The paragraph explains how the rates of change for each category are determined by the interactions between them and external factors like social distancing and recovery rates. It also touches on the use of phase portraits and simulations to understand disease dynamics without solving the equations explicitly, providing a foundation for further exploration of population dynamics and disease modeling.

Keywords

💡Differential Equations

Differential equations are mathematical equations that involve derivatives, which describe the rates at which quantities change in relation to one another. In the video, they are presented as fundamental tools for modeling natural phenomena and understanding the universe's workings. Examples include modeling population growth, fluid dynamics, and electromagnetism, all of which are integral to the video's theme of demonstrating the omnipresence and utility of differential equations in real-world applications.

💡Maxwell's Equations

Maxwell's Equations are a set of four fundamental equations in electromagnetism that describe how electric and magnetic fields are generated and altered by each other and by charges and currents. The video mentions these equations as an example of differential equations that underpin technologies like phones, radio, Wi-Fi, and GPS, highlighting their critical role in modern communication systems.

💡Pursuit Curves

Pursuit curves represent the path traced by an object chasing another. The video uses the concept in the context of a TV show 'Numbers' to illustrate how differential equations can predict the movement of criminals being pursued by the FBI. This concept is also applicable to various real-world scenarios like missile guidance systems and aircraft maneuvers, emphasizing the practicality of differential equations in tracking and prediction.

💡SI Model

The SI model is a simple mathematical model used in epidemiology to describe the spread of infectious diseases within a population. In the video, it is used to explain how the susceptible (S), infected (I), and recovered (R) populations interact, with differential equations describing the flow of individuals between these categories. The model is crucial for understanding the dynamics of disease spread, as illustrated by the video's discussion on the coronavirus pandemic.

💡Epidemiology

Epidemiology is the study of the distribution and determinants of health-related events or states in specified populations. The video touches on this field when discussing the SI model and its application to model the spread of the coronavirus. Epidemiology uses differential equations to predict and control outbreaks, showcasing the practical application of mathematical modeling in public health.

💡Vector

In mathematics and physics, a vector is a quantity that has both magnitude and direction. The video uses vectors to represent the positions and velocities of objects in pursuit curves, illustrating how the mathematical properties of vectors can be used to model and analyze motion in pursuit scenarios, such as the chase between the FBI and criminals in the 'Numbers' TV show.

💡Dot Product

The dot product is an algebraic operation that takes two equal-length vectors and returns a single number. In the video, it is used in the context of pursuit curves to normalize vectors and establish a relationship between the velocity of the pursuing object and the direction towards the target. This operation is key to formulating the differential equation that models the pursuit scenario.

💡Normalization

Normalization is the process of scaling a vector to have a length of one, without changing its direction. The video demonstrates this process when dealing with vectors in pursuit curves, emphasizing its importance in simplifying the mathematical model and facilitating the calculation of the dot product, which is essential for deriving the differential equation.

💡Second-Order Nonlinear Differential Equation

A second-order nonlinear differential equation is a differential equation where the second derivative of the unknown function appears multiplied by a nonlinear function of the function itself or its derivatives. The video introduces such an equation when discussing the motion of a barbell with chains, illustrating the complexity that arises when dealing with changing mass in physical systems.

💡Phase Portrait

A phase portrait is a graphical representation used in the study of differential equations to visualize the behavior of a system over time. The video mentions phase portraits in the context of population dynamics, suggesting their utility in understanding the long-term behavior of populations without necessarily solving the underlying differential equations.

💡Brilliant

Brilliant is an educational platform that offers courses on various subjects, including differential equations. The video is sponsored by Brilliant and features a promotion for their courses on differential equations, which focus on real-world applications. The platform is presented as a resource for learning and understanding the concepts discussed in the video, such as pursuit curves and wave equations.

Highlights

Differential equations are fundamental in describing how nature and the universe work.

They are often challenging to solve but provide valuable insights into various phenomena.

Differential equations are used to model population growth, fluid dynamics, and electromagnetism, including the principles behind phones, radio, Wi-Fi, and GPS.

Maxwell's equations, consisting of four differential equations, are key to understanding electromagnetism.

Differential equations can describe motion with or without physical contact, such as the orbits of celestial bodies.

They can be given meaning by interpreting the story they tell, like relating to the area under a curve and its arc length.

An example of a pursuit curve from the TV show 'Numbers' demonstrates how differential equations can be applied to real-world scenarios like law enforcement tracking criminals.

Pursuit curves illustrate the path of one object chasing another and can be mathematically modeled using differential equations.

The video explains the mathematical process of determining the curve traced by a pursuing object, involving assumptions about the chase dynamics.

Differential equations are used to model the changing weight experienced during an exercise with chains, such as bench press or squat.

The motion of lifting a chain is represented by a second-order nonlinear differential equation, highlighting the complexity of seemingly simple movements.

The concept of changing mass in a system, like a rocket losing mass as it exhausts, leads to differential equations that describe its motion.

The spread of the coronavirus is modeled using differential equations, illustrating how the infection rate changes over time.

The SIR model is introduced as a basic framework to understand the dynamics of disease spread in a population.

Differential equations are essential in modeling population growth, including complex interactions between different species or factors.

Phase portraits are mentioned as a tool for visualizing the behavior of systems described by differential equations without needing an explicit solution.

Brilliant.org offers courses on differential equations that focus on real-world applications, including pursuit curves, wave equations, and beam behavior.

The video concludes with an invitation to learn more about differential equations and their practical uses through Brilliant's courses, offering a discount for the first 200 subscribers.

Transcripts

this video is sponsored by brilliant

let's just get to the point why do we

learn differential equations because

they are the equations that describe how

nature works the universe one day said

boom here's a bunch of stuff and we said

cool how does it all work and the

universe said differential equations

they're tough often impossible to solve

exactly but you'll eventually get some

cool stuff from them modeling how a

population will grow involves

differential equations how any fluid

moves differential equations

electromagnetism which is how phones

radio Wi-Fi and GPS all work not one but

four differential equations known as

Maxwell's equations there's electric

circuits and even if something touches

something else and thus exerts a force

differential equations are used to

describe the motion if there's no

physical contact like with orbiting

bodies there's still a force so there's

still differential equations now as with

simple algebraic equations differential

equations can and often do have meaning

when you read into the story that

they're telling like this equation could

be saying my age is y and I'm exactly

five years older than my brother whose

age is X and we can use this to

determine either of our ages given the

other pretty boring but we can give it

meaning this equation can have meaning

too or rather it asked the question and

that question is what curve or family of

curves have the property where the

numerical value of the area under the

curve is twice numerical value of the

arc length on that same interval for any

given interval A to B

well to set this up we start with this

equation which is the area under the

curve itself and this is the equation

for the arc length on that same interval

A to B but we want to know when the left

side always equals twice the right side

now we can differentiate both sides to

remove the integral sign and we're left

with a differential equation from here

we can square both sides and then

distribute and we get that original

equation if you solve for that function

y you get this which is the curve you're

seeing here so that's one example of

meaning within a differential equation

but let's see how these really describe

some real-world situations because it's

not always obvious what story these

equations tell or how they show up in

general and since I always love bringing

up the tv-show numbers when I can here's

a perfect example so check out this

scene from an episode where law

enforcement is trying to catch a couple

committing crimes as they travel across

the United States we plot your movements

against those targets the pattern makes

itself known and when we plot your path

against oil and winters we got this yeah

this is the Red Desert Robbery the

missing point on a curve that I didn't

even realize I was looking at it's a

variation on something called a pursuit

curve alright so what's happening here

is the FBI has been chasing this couple

across the country but hasn't caught

them yet so the mathematicians plotted

the path both the criminals and the FBI

took to see if they can make some

predictions about where the criminals

will strike next and this is related to

pursuit curves a pursuit curve is simply

the curve traced out by one object

chasing another although there are

usually conditions listed for something

to be technically considered a pursuit

curve

but this could apply to a cheetah

chasing down a gazelle or one aircraft

chasing another for example so let's see

how we can determine the curve that the

pursuing object will trace act now two

things to note first we're going to

assume that the plane being chased has a

predetermined path whether it's flying

straight up or in a circle or whatever

assume we already know their path then

the second assumption like I mentioned

before is that the chasing object is

always moving in the direction of the

other and it turns its nose as needed

during pursuit in reality this could be

like a plane wanting it's forward-facing

guns always aimed at the target or

something anyways what you're seeing

here is a snapshot of the chase and we

can represent the current positions of

each plane with a vector I'll say C and

M for cat and mouse the other thing we

know is that at this time or really any

time the chasing plane is pointed at the

front one which means this is their

velocity vector or C prime at this

moment there's no wind or anything so

the plane is definitely flying in the

direction it's pointed now we don't know

the speed or the length of that vector

currently but we know the direction at

least that's more important because

there's another vector pointing in that

same direction which is easy to find and

that's M minus C for the visualization M

minus C is the same as M plus negative C

and putting negative C on top of M gives

us a vector that points from the back

plane to the front one

then to deal with the lengths I'm gonna

normalize the two vectors by dividing by

their magnitudes so they both have a

length of one this is key because the

dot product of two vectors both with

length one and pointing in the same

direction is one this is a fundamental

equation yes I could have just set the

vectors equal to one another but I'm

doing this because in that episode when

the mathematician is explaining pursuit

curves you can see that equation come on

the screen so now you know the meaning

behind it but still it's not really

obvious how to solve it yet but if we go

back to our snapshot remember that the N

vector is actually a known function of

time we're seeing it only at one moment

in time but it is changing as the planes

fly around so I'll say it's a vector

function U of T comma V of T which are

both known I'm just keeping things

generic the C vector also changes in

time but it's our unknown some X of T

comma Y of T that we want to solve for

and the C prime vector would just be X

prime of T comma Y prime of T so then M

minus C would give us this vector here

just the X components subtracted and the

Y components subtracted and I'm just not

writing the t's so there's room I'll do

the same thing with C prime then if we

plug all of those into our equation that

we want to solve we get this now the one

extra thing I did was set the magnitude

of C prime to 1 which just means we

assumed the chasing plane is flying at a

constant speed of 1 just to simplify the

equation then we just have to do the dot

product which leaves us with this

differential equation

you'll notice I actually wrote out the

expression for the magnitude of M minus

C on the bottom here the only problem

with this is that there are two unknown

functions x and y which means we need

another equation but that would just be

the one saying the chasing plane is

flying at a constant speed of 1 now we

have a system of differential equations

that can be solved if for example we

assumed the target plane is flying

straight along the y axis then this

would be the path of the chasing plane

shown in red if the target plane we're

flying in a circle then you get

something very different shown here on

brilliant sight now you'll notice this

method of chasing someone isn't

necessarily ideal for catching them but

there seems to be other types or

variations of pursuit curves that range

from always aiming at the target to

predicting where they'll go next on that

numbers episode the situation was more

complex as the mathematicians were

accounting for how the Meuse of the FBI

might affect the criminals that were

being chased but still the basics of

pursuit curves can be seen in a first

level differential equations course and

while this might not be a real-world FBI

case pursuit curves can be applied to

missile guidance systems aircraft

submarines and so on all right now let's

look at something more casual if you go

to the gym you may have seen or done a

bench press or squat with chains hanging

off the sides this makes it so that as

the bar moves up the chain is more and

more suspended and this contributes more

of its weight to the exercise meaning as

the person pushes upwards the weight

increases this actually complicates the

equation of motion more than you might

think

because for every little DX or change in

height yes I'll be using X as the

variable there's a DM or small change in

mass in regards to the part of the chain

that's off the ground so let's see what

this set up would look like

now we'll say the barbell has no mass

just to make things easier so really

we're just lifting the chain off the

ground and we'll call that distance off

the ground X measured in meters then

let's give the chain a way to density of

10 Newton's per meter

thus the weight of just the section off

the ground is 10 X so if the chain were

2 meters off the ground then you'd have

to use a force of 20 Newtons to hold it

in place then the equation for mass for

the part of the chain off the ground is

simply the weight divided by gravity

weight is 10x and I'll round gravity to

10 as always so the mass of this part of

the chain off the ground is just X

lastly we'll say the person is pushing

up with a constant force of 50 Newtons

meaning the net force is 50 up minus the

10x down from the chain itself okay now

before we can move on we have to realize

that F equals MA is a lie well not

really but it only applies to special

cases where the mass is constant the

real equation we have to work with is f

equals the rate of change of momentum or

mass times velocity doing a simple

product rule we get this here and you'll

notice when M is not changing which we

get used to in a first level physics

course then this term is zero and we're

left with F equals m times dv/dt or F

equals MA as usual but with the changing

mass we have this entire equation from

here I'm just going to replace the

variables like mass is really X and

force is 50 minus 10x so we get this

here but velocity is just the rate of

change of position and DV DT which is

acceleration is the second derivative of

position so we're left with this

equation here moving the 10x over we're

left with a second order nonlinear

differential equation solving this would

not be easy but not really the point of

this video instead I just want to

highlight that the motion which results

by something as simple

pulling a chain upwards has to be

expressed through a not so simple second

order differential equation and while it

may be true that analyzing the motion of

a barbell isn't too applicable the idea

of analyzing a system with changing mass

is the perfect example is a rocket as

exhaust leaves the bottom the rocket

itself loses mass little by little so

thrust and a changing mass are kind of

linked and the situation also leads to

differential equations but now let's

look at the most real-world application

I can think of this here is a curve of

the number of currently infected people

from the corona virus as of early June

it's infected people versus time which

means the instantaneous rate of change

or slope at any point is di DT it

gradually increased for a while before

flattening out but we want that rate of

change to go negative anyways this is an

incomplete picture of what's going on

because there are other categories of

people out there in the population there

those that have never been infected or

those that are susceptible those that

are currently infected and then those

that are recovered or unfortunately

deceased but the most basic model the SI

R model just calls it recovered and

assumes no deaths I know many youtubers

have talked about this recently so I'll

keep it kind of short in the case of the

corona virus everyone started in the

susceptible bucket and let's say the

population is 20 so no one is infected

but everyone has the potential to be and

then one day one person transition to

infected this was basically an initial

condition now if the population stays

constant no one new is born then the

number of susceptible people can only go

down or stay the same because as soon as

you get infected you leave that group

never to return

assuming immunity after you get the

disease so the rate of change of

susceptible people is going to be

negative something it can only go down

since having a lot of infected people or

a lot of susceptible people / a high

population

increases the magnitude of that change

then we say it's s times I where s and I

are the number of susceptible and

infected people respectively if either

of these are large and the other is

nonzero you have a large transition to

those who are infected but we also have

to include a constant that constant

depends on the virus and us as it scales

how quickly people go from healthy to

sick social distancing or hand-washing

for example would decrease that constant

and this rate of change wouldn't be as

extreme then the rate of change of those

who are infected starts with that same

expression seen on the left but positive

this is because in this model it's a

one-way street if someone leaves the

susceptible pile they go to infect it

but people will leave the infected pile

proportional to how many infected people

there are this constant in reality is

death rate combined with recovery rate

if medicine is released that speeds up

recovery by 50% and that constant goes

up and people are quicker to leave the

infected pile and become recovered the

rate of change of those who have

recovered can only be positive or zero

and it's that same constant times I

you'll notice in this model that we kept

the population constant so the sum of

the three categories was always the same

meaning the rates of change should add

to zero as they do but here we're left

with another system of differential

equations that when solved will tell you

how an infection will spread through a

population in this simplified scenario

I'm sure many of you have seen number

files video on this that I'll link below

but there you can see what happens when

you play around with the equations and

constants and all that as with most of

these examples we did simplify things to

make the math easier but this is all the

foundations of what's going on in the

real world if you go to the website for

the International Council for industrial

and applied mathematics there's a page

on the mathematics of koban 19 showing

the simulations and models that

mathematicians are creating to

understand the spread of this virus in

different parts of the world where

you'll find equation

just like we saw equations very similar

to these also show up in terms of

population growth one of the first

differential equations a lot of us learn

is the one that models how a population

will grow at a rate proportional to its

current value the more people or animals

there are the faster the growth as

expected but things get more complicated

with deaths or when maybe one population

kills off another here's an example of

bacteria which can multiply on their own

and phages

that essentially feed off bacteria and

thus will die without them and you'll

see that after one cycle here the phages

grow from 1 to 4 but the bacteria stay

at 2 and now there are more phages so

some will die while others will continue

to multiply so there's kind of this

back-and-forth that happens but it leads

to differential equations where the

rates have changed depend on multiples

of the populations and it's not always

about just solving the equations as

there are tools such as phase portraits

that can help paint a picture about

what's going on without having to find

an actual solution here if you're given

a certain population of phages and

bacteria this would tell you how the

system or really both populations will

change at that moment and with this we

can find equilibrium points or long term

behavior for example and while I'm not

gonna go any further than this think

we've discussed a lot if you want to

dive more into the topic of differential

equations you can of course do so right

here at brilliant currently they have

two differential equations courses which

are some my favorites because of how

much they focus on real-world

applications they have the pursuit

curves we discussed there's 2d and 3d

wave equations

there's the equations that model the

behavior of beams and much more their

first course does start at the basics

for anyone just starting out but by the

second course there are things I never

saw as an engineer in college so

regardless of where you are in your

education there likely is a lot to learn

whether you want to get ahead as a

student or just brush up on old topics

so if you want to get started right now

support the channel you can click the

link below or go to brilliant org slash

Zack star plus the first 200 people to

sign up will get 20% off their annual

premium subscription and with that I'm

going to end that video there thanks as

always my supporters on patreon social

media links to follow me are down below

and I'll see you guys in the next video