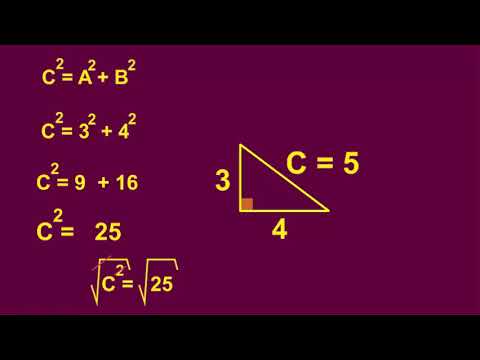Todas las posibles ternas pitagóricas, visualizadas

3Blue1Brown Español

8 Aug 201816:08

Summary

TLDREste video explica el teorema de Pitágoras y cómo se relaciona con las ternas pitagóricas, que son conjuntos de tres números enteros donde la suma de los cuadrados de los dos menores es igual al cuadrado del mayor. Se muestra un método para generar estas ternas utilizando números complejos y se exploran diversas propiedades matemáticas. También se menciona la historia y la importancia del teorema en la matemática antigua, y se incluye una demostración visual y algebraica del teorema. Finalmente, se discute la relación con los puntos racionales en un círculo unitario.

Takeaways

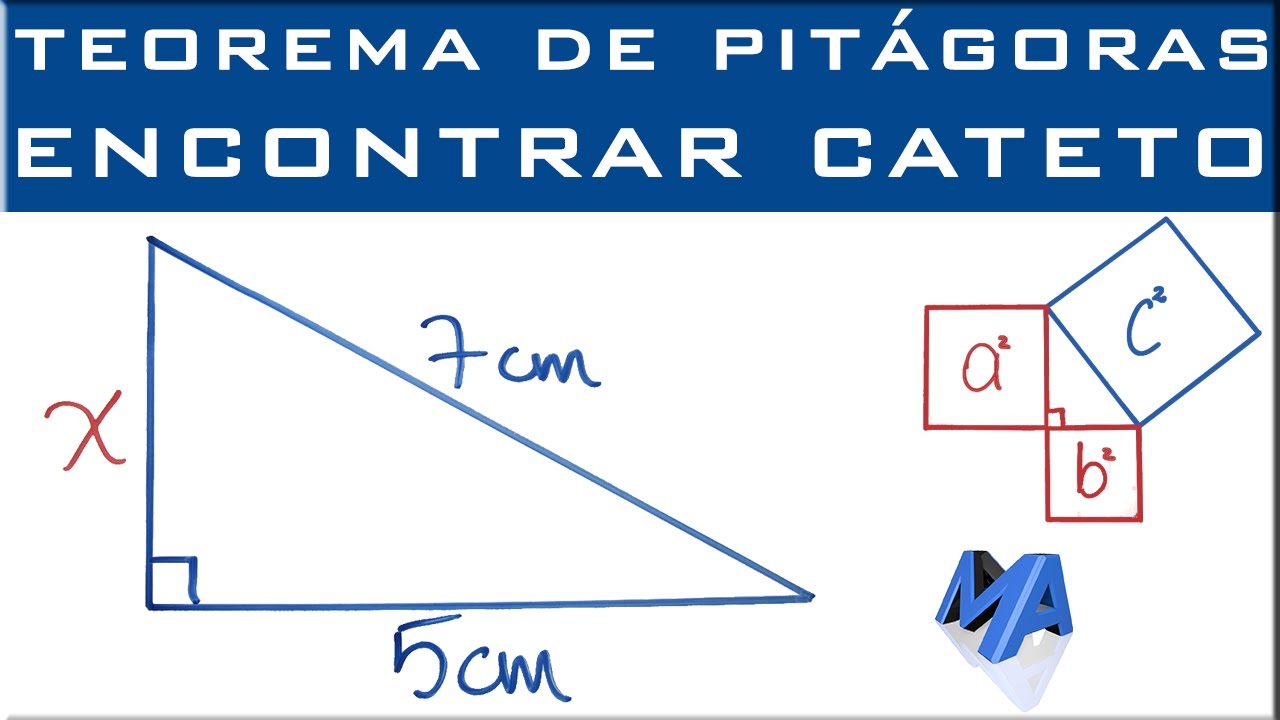
📚 El Teorema de Pitágoras afirma que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
🔍 Se menciona que existen ejemplos de triángulos rectángulos con longitudes de los catetos y la hipotenusa que son números enteros, como el triángulo 3-4-5.
📐 Se destaca que hay casos en los que la suma de dos cuadrados perfectos resulta en otro cuadrado perfecto, pero esto no ocurre para exponentes mayores que 2, haciendo referencia al último teorema de Fermat.
🔢 Se define una terna pitagórica como un conjunto de tres números enteros (a, b, c) donde (a^2 + b^2 = c^2).
📘 Se menciona la antigüedad del problema, con referencia a tabletas babilónicas de 1800 a.C. que listan ternas pitagóricas.
🎨 Se comparte una demostración visual del teorema de Pitágoras, usando cuadrados y triángulos para representar la relación entre los catetos y la hipotenusa.
📍 Se establece una relación entre encontrar ternas pitagóricas y puntos de la rejilla con coordenadas enteras que están a una distancia entera del origen.
🧩 Se describe un método para generar ternas pitagóricas no triviales a través de la multiplicación de números complejos y su representación en el plano complejo.
📉 Se discute cómo la elevación al cuadrado de puntos de la rejilla puede resultar en nuevas ternas pitagóricas, y cómo algunos puntos pueden generar múltiples soluciones.
🔄 Se muestra cómo el método de elevación al cuadrado puede ser utilizado para visualizar y comprender la distribución de las ternas pitagóricas en el plano complejo.
🔍 Se cuestiona la completitud del método, argumentando que todos los puntos racionales en el círculo unitario deberían ser alcanzables para garantizar que se encuentran todas las ternas pitagóricas posibles.

Q & A

¿Qué dice el teorema de Pitágoras?
-El teorema de Pitágoras establece que la suma de los cuadrados de los catetos en un triángulo rectángulo es igual al cuadrado de la hipotenusa.
¿Qué es una terna pitagórica?
-Una terna pitagórica es un conjunto de tres números enteros (a), (b) y (c) que cumplen con la ecuación (a^2 + b^2 = c^2).
¿Cuál es el método presentado en el video para encontrar ternas pitagóricas?
-El método consiste en elevar al cuadrado un número complejo con coordenadas enteras para generar una terna pitagórica.
¿Cómo se relacionan las ternas pitagóricas con los puntos en el plano?
-Encontrar ternas pitagóricas es equivalente a encontrar puntos en el plano con coordenadas enteras que estén a una distancia entera del origen.
¿Qué es un número complejo en el contexto del video?
-Un número complejo en el contexto del video se refiere a un punto en el plano complejo representado como (a + bi), donde (a) y (b) son números enteros.
¿Qué sucede cuando se eleva al cuadrado un número complejo?
-Al elevar al cuadrado un número complejo, se duplica el ángulo con la horizontal y se eleva al cuadrado su longitud, resultando en una nueva terna pitagórica.
¿Cuál es la importancia de los múltiplos de ternas pitagóricas en el método presentado?
-Los múltiplos de ternas pitagóricas se incluyen dibujando líneas desde el origen a través de los puntos generados, asegurando que no se omitan ternas pitagóricas que son múltiplos de otras ternas.
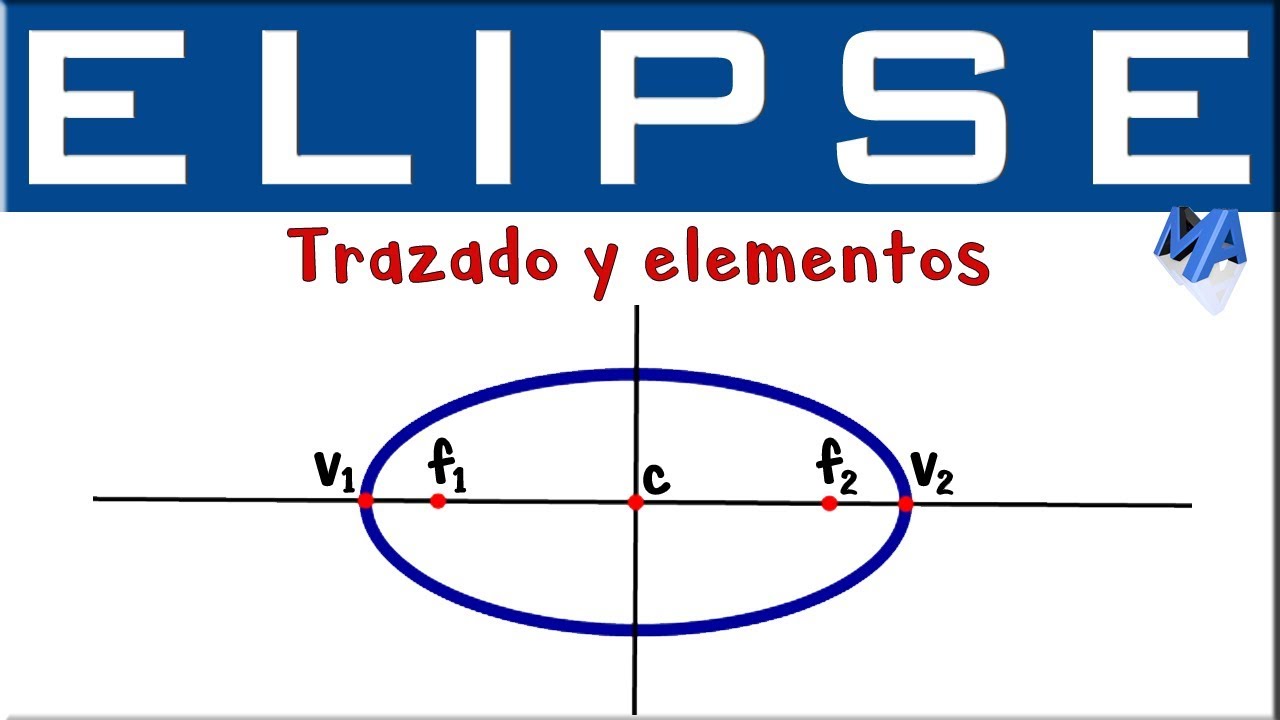
¿Cómo se relaciona el círculo unitario con las ternas pitagóricas?
-Al dividir la ecuación (a^2 + b^2 = c^2) por (c^2), se obtiene una ecuación que representa un punto en el círculo unitario con coordenadas racionales.
¿Por qué es importante que el método genere todas las pendientes racionales?
-Generar todas las pendientes racionales asegura que se encuentren todos los puntos racionales en el círculo unitario, garantizando que se generen todas las ternas pitagóricas posibles.
¿Qué relación hay entre las ternas pitagóricas y los puntos racionales en el círculo unitario?
-Cada terna pitagórica corresponde a un punto racional en el círculo unitario, y encontrar todos los puntos racionales en el círculo garantiza encontrar todas las ternas pitagóricas.

Outlines

00:00

📐 Introducción al Teorema de Pitágoras

Se presenta el Teorema de Pitágoras, explicando que la suma de los cuadrados de los catetos en un triángulo rectángulo es igual al cuadrado de la hipotenusa. Se mencionan ejemplos clásicos como los triángulos 3-4-5 y 5-12-13, y se introduce el Último Teorema de Fermat, que afirma que no hay soluciones enteras para exponentes mayores que 2. Además, se introduce el concepto de terna pitagórica.

05:01

🔍 Visualización de Ternas Pitagóricas

Se explica cómo encontrar todas las posibles ternas pitagóricas, mencionando la historia antigua de las matemáticas con tabletas babilónicas que ya listaban estas ternas. También se presenta una prueba visual del Teorema de Pitágoras usando cuadrados construidos en los lados de un triángulo. Luego, se reformula el problema de encontrar puntos de coordenadas enteras que estén a una distancia entera del origen en el plano complejo.

10:03

🔢 Generación de Ternas Pitagóricas

Se detalla un método para generar ternas pitagóricas utilizando números complejos. Al elevar al cuadrado un número complejo con coordenadas enteras, se obtiene una nueva terna pitagórica. Se ejemplifica este proceso con varios puntos, mostrando cómo al elevar al cuadrado se obtiene una terna. Se menciona que algunas ternas triviales pueden aparecer, pero el método en general es efectivo.

15:04

✨ Visualización Elegante de Ternas Pitagóricas

Se destaca cómo este método de elevar al cuadrado números complejos organiza las ternas pitagóricas de manera estructurada y visible en el plano complejo. Se explica que aunque algunas ternas no aparecen directamente, son múltiplos de otras ternas generadas por el método. Se utiliza una visualización de líneas radiales para incluir todos los múltiplos posibles y se proyectan estos puntos en un círculo unitario.

🎯 Completitud del Método y Conclusiones

Se concluye que el método de elevar al cuadrado números complejos genera todas las ternas pitagóricas posibles, al incluir todas las pendientes racionales en el círculo unitario. Se proporciona una explicación geométrica de por qué esto es así, asegurando que todos los puntos racionales del círculo unitario son cubiertos. Finalmente, se menciona un patrocinador que trabaja en optimización del transporte público, relacionando el contenido matemático con aplicaciones prácticas.

Mindmap

Keywords

💡Teorema de Pitágoras

El Teorema de Pitágoras es un principio matemático fundamental que afirma que en un triángulo rectángulo, la suma de las áreas de los cuadrados de los catetos es igual al área del cuadrado de la hipotenusa. En el video, se utiliza este teorema para introducir el concepto de ternas pitagóricas y se da un ejemplo de cómo se aplica en triángulos como el 3-4-5.

💡Terna pitagórica

Una terna pitagórica es un conjunto de tres números enteros, a, b y c, que satisfacen la ecuación a^2 + b^2 = c^2. Estas ternas son centrales en el video, donde se busca encontrar y visualizar todas las posibles combinaciones de números que cumplen con esta relación.

💡Último teorema de Fermat

El Último teorema de Fermat es un famoso problema de matemáticas que se menciona en el video para contrastar con el teorema de Pitágoras. A diferencia de las ternas pitagóricas, el teorema de Fermat establece que no existen soluciones enteras para ecuaciones de la forma a^n + b^n = c^n, cuando n es mayor que 2.

💡Plano complejo

El plano complejo es un concepto matemático que se introduce en el video para explicar una técnica para generar ternas pitagóricas. Se utiliza para representar los puntos de la rejilla como números complejos y, al elevarlos al cuadrado, se garantiza que la distancia del origen sea un número entero.

💡Números complejos

Los números complejos son números que consisten en una parte real y una parte imaginaria, separadas por una 'i'. En el video, se usan para representar los puntos de la rejilla y manipularlos algebra y geométricamente para encontrar ternas pitagóricas.

💡Pendiente racional

La pendiente racional se refiere a una pendiente de una línea cuyo valor es un número racional. En el video, se argumenta que todas las pendientes racionales son posibles en el método de elevar números complejos al cuadrado, lo que asegura que se encuentren todos los puntos racionales en el círculo unitario y, por ende, todas las ternas pitagóricas.

💡Círculo unitario

El círculo unitario es un círculo cuyo radio es 1 y que se utiliza en el video para representar los puntos que tienen una distancia unitaria del origen. Se relaciona con las ternas pitagóricas al mostrar que cada punto en el círculo unitario puede corresponder a una terna pitagórica.

💡Racional

Un número racional es cualquier número que puede ser expresado como la relación de dos enteros, donde el denominador no es cero. En el contexto del video, los puntos racionales son aquellos que tienen coordenadas que son números racionales y son clave para encontrar todas las ternas pitagóricas.

💡Múltiplos de ternas pitagóricas

Los múltiplos de ternas pitagóricas son aquellas que se obtienen al multiplicar cada componente de una terna pitagórica por el mismo número entero. El video discute cómo ciertos múltiplos pueden 'escapar' del método de generación de ternas pitagóricas, pero se sugiere una forma de incluirlos al trazar líneas desde el origen a través de puntos específicos.

💡Geometría del círculo

La geometría del círculo es utilizada en el video para demostrar por qué el método de elevar números complejos al cuadrado produce todas las pendientes racionales posibles. Se menciona que el ángulo entre dos puntos de la circunferencia y su centro es el doble del ángulo entre esos puntos y cualquier otro punto de la circunferencia, lo que ayuda a justificar la completitud del método propuesto.

Highlights

El teorema de Pitágoras afirma que la suma de los cuadrados de los catetos en un triángulo rectángulo es igual al cuadrado de la hipotenusa.

Se mencionan ejemplos clásicos de triángulos pitagóricos como 2-3-4 y 5-12-13.

Existen casos en los que la suma de dos cuadrados perfectos es otro cuadrado perfecto.

Cambio del exponente a un número entero mayor que 2 conduce a la pérdida de soluciones enteras, relacionado con el último teorema de Fermat.

Se define una terna pitagórica como una terna de números enteros (a, b, c) donde a^2 + b^2 = c^2.

Se discuten las antiguas tabletas babilónicas que listan ternas pitagóricas, predatando a Pitágoras.

Se comparte una demostración favorita del teorema de Pitágoras usando cuadros y triángulos.

Se reformula la búsqueda de ternas pitagóricas en términos de puntos de la rejilla con distancias enteras del origen.

Se introduce el concepto de plano complejo para facilitar la generación de ternas pitagóricas.

Se describe el proceso de elevar al cuadrado números complejos para obtener nuevas ternas pitagóricas.

Se ilustra cómo la multiplicación compleja puede ser vista tanto algebraica como geométricamente.

Se da un ejemplo práctico de cómo multiplicar un número complejo por sí mismo resulta en un triángulo pitagórico.

Se anima a los espectadores a experimentar con el método para encontrar triángulos pitagóricos.

Se discute cómo algunos resultados son triviales, como cuando las coordenadas del punto inicial son iguales o una es cero.

Se presenta una fórmula elegante para generar ternas pitagóricas a partir de coordenadas de puntos de la rejilla.

Se visualiza el movimiento de puntos en el plano complejo hacia su cuadrado, ilustrando la generación de ternas pitagóricas.

Se analiza la representación de puntos de la rejilla en el círculo unitario y su relación con ternas pitagóricas.

Se argumenta que el método de elevar al cuadrado de números complejos produce todas las pendientes racionales posibles.

Se concluye que el método propuesto garantiza encontrar todas las ternas pitagóricas posibles.

Se menciona Remix, una plataforma de planificación para el transporte público, en busca de ingenieros de software con experiencia en matemáticas.