The Key Definitions of Differential Equations: ODE, order, solution, initial condition, IVP
Summary
TLDRThis educational video delves into the fundamentals of differential equations, introducing the concept with a specific example and explaining the terminology of ordinary versus partial differential equations. It emphasizes the importance of the order of a differential equation and illustrates how to identify and verify solutions, including the use of technology like the Maple Calculator app. The script also touches on initial value problems, showcasing how to find specific solutions given certain conditions, and encourages viewers to explore the fascinating world of differential equations.
Takeaways
- 📚 The video is part of a series on differential equations, introducing major concepts and providing access to a full course and open source textbook.
- 🔍 The script provides a formal definition of a differential equation, emphasizing its components such as variables, derivatives, and the relationship between them.
- 📉 The concept of 'order' in differential equations is introduced, highlighting that it refers to the highest derivative present in the equation.
- 📈 The difference between ordinary and partial differential equations is explained, with the former involving a single independent variable and the latter involving multiple variables and partial derivatives.
- 🔑 The script discusses the idea of solving differential equations, illustrating how certain functions can satisfy a given differential equation and be considered solutions.
- 🔍 The process of finding solutions to differential equations is mentioned, with the promise of exploring methods in later videos of the course.
- 🌐 The use of technology, specifically the Maple calculator app, is showcased as a tool for solving differential equations by interpreting handwritten or typed equations.
- 📝 The script introduces the concept of a general solution, which contains all possible solutions to a differential equation, typically represented with arbitrary constants.
- 🔑 The importance of initial conditions in defining a specific solution to a differential equation is highlighted, transforming a general solution into a particular one.
- 📈 The notion of an initial value problem is explained, which involves a differential equation and specific initial conditions to find a unique solution.
- 📚 The video concludes by emphasizing the foundational terminology and concepts introduced, setting the stage for further exploration in the course.
Q & A
What is the main topic of the video?
-The main topic of the video is differential equations, focusing on introducing the major ideas and concepts related to this mathematical field.
What is the difference between an ordinary differential equation and a partial differential equation?
-An ordinary differential equation involves derivatives with respect to a single independent variable, while a partial differential equation involves partial derivatives with respect to multiple variables.
What is the order of a differential equation?
-The order of a differential equation is the highest derivative that appears in the equation. For example, if the highest derivative is the third derivative, the order is 3.
What is the purpose of solving a differential equation?
-The purpose of solving a differential equation is to find the function or functions that satisfy the given equation, which can describe various phenomena in science and engineering.
How does the video illustrate the concept of a solution to a differential equation?
-The video illustrates the concept by providing examples of functions, such as e^t and c1e^t + c2e^(3t), that when substituted into the differential equation, satisfy the equation, thus qualifying as solutions.
What is the general solution to a differential equation?
-The general solution to a differential equation is an expression that contains every possible solution to the equation, often involving arbitrary constants that can take on different values.
What is an initial value problem in the context of differential equations?
-An initial value problem is a differential equation supplemented with initial conditions, which are specific values of the function and its derivatives at a given point, usually at t=0.
How does the video mention the use of technology to solve differential equations?
-The video mentions the use of the Maple Calculator app, which can interpret handwritten or typed differential equations and provide the general solution.
What is the significance of the arbitrary constants in the general solution of a differential equation?
-The arbitrary constants in the general solution allow for the representation of an infinite family of solutions, as they can take on any value, thus capturing all possible solutions to the equation.
How does the video define the solution to an ordinary differential equation?
-The video defines a solution to an ordinary differential equation as a specific function that, when substituted into the equation, satisfies the equation for all values of the independent variable.
What is the role of initial conditions in solving an initial value problem?
-Initial conditions in an initial value problem provide specific values for the function and its derivatives at a certain point, which helps in determining the particular solution that satisfies both the differential equation and the initial conditions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Fisika Komputasi - Metode Finite Difference 05 Sifat Diferensial dan Persamaan Diferensial

Persamaan Diferensial Parsial (Pengertian, Definisi, dan Klasifikasi)

Introduction to Differential Equations (Differential Equations 2)

GRINGS - Equações Diferenciais Ordinárias - Aula 1

Pengantar Persamaan Diferensial
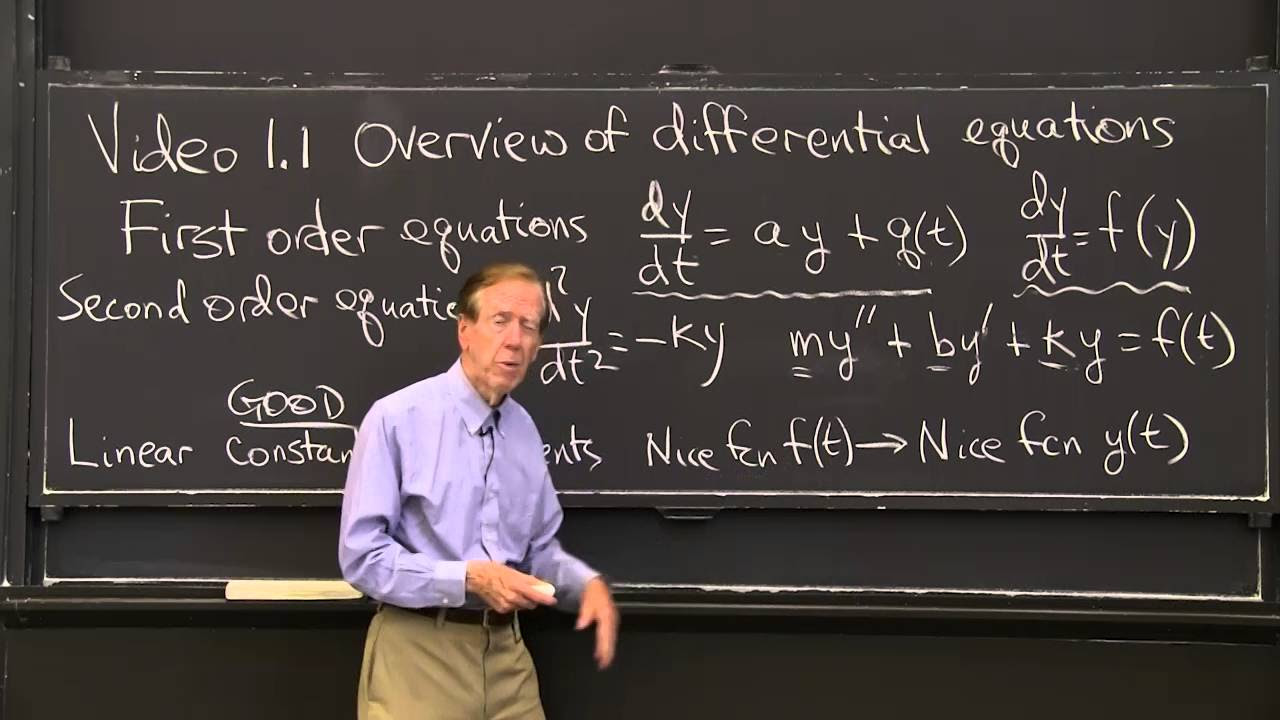
Overview of Differential Equations
5.0 / 5 (0 votes)