Application of Mean, Median and Mode [In Real Life] [Uses in Real Life]

Summary

This video explores the appropriate use of mean, median, and mode in data analysis. It explains these measures of central tendency and their applications in real-life scenarios, using examples to illustrate when each is most effective. The video emphasizes the importance of data distribution and the presence of outliers in choosing the right statistical measure, offering practical tips for personal and professional decision-making.

Takeaways

• 📊 Mean, median, and mode are summary statistics used to analyze and summarize data sets.
• 🔢 The mean is the arithmetic average of all values, but it can be skewed by outliers.
• 📈 Median is the middle value in a data set and is less affected by extreme values.
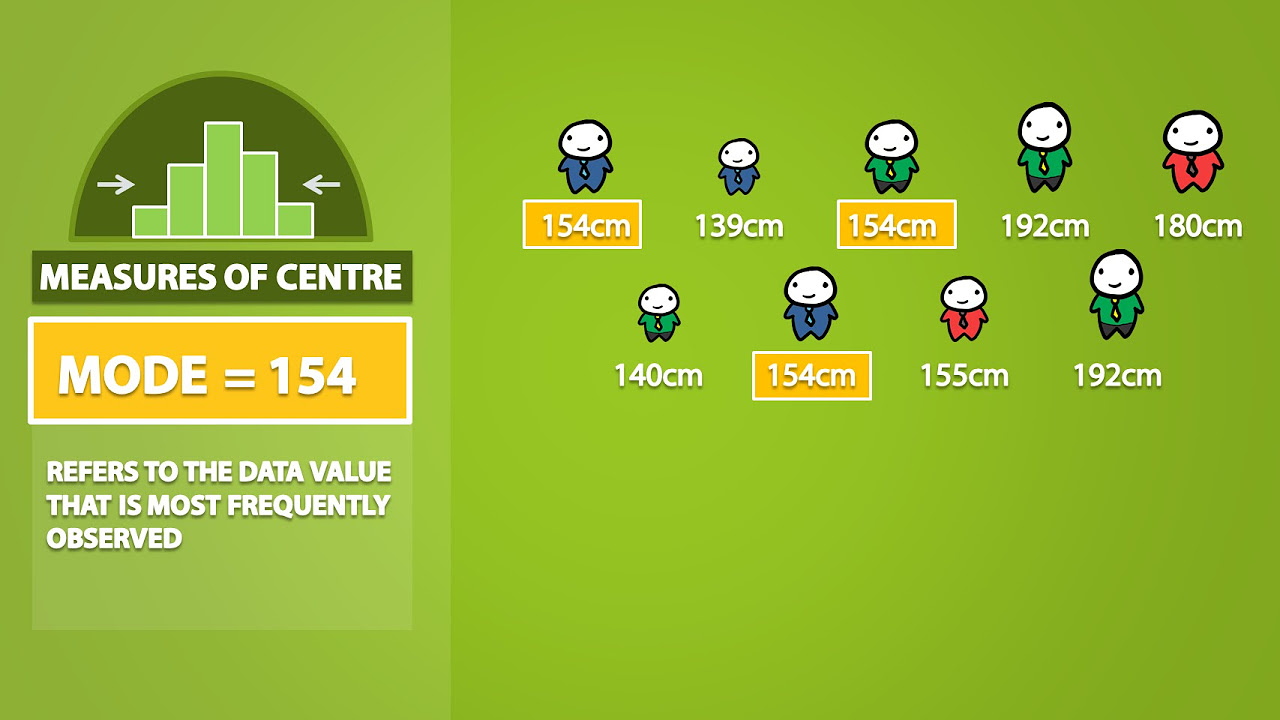
• 🍦 Mode is the most frequently occurring value in a data set, useful for categorical data.
• 📚 It's important to choose the right measure of central tendency based on the data's distribution and characteristics.
• 📉 Outliers can significantly affect the mean, making it less representative of the overall data set.
• 🌾 In skewed data sets, like exam scores or agricultural output affected by drought, the median can provide a better summary.
• 🍹 For evenly distributed data, such as monthly sugar usage in a manufacturing process, the mean can be a reliable summary statistic.
• 👠 Retailers can use mode to identify the most popular shoe sizes to stock based on sales data.
• 🏠 Mode can also be applied in everyday life, such as organizing household items based on frequency of use.
• 📋 The script provides a comparison table to help decide when to use mean, median, or mode based on the data's characteristics.

Q & A

What are the three main summary statistics discussed in the video?

The three main summary statistics discussed in the video are mean, median, and mode.

Why might the mean not be the most appropriate measure to summarize data?

The mean might not be the most appropriate measure to summarize data when there are extreme values or outliers, as it can skew the average and provide a misleading representation of the data set.

What is the definition of the median in statistics?

The median is the middle value in a data set when all the observations are arranged in ascending or descending order. It divides the data into two equal halves.

Can you provide an example from the script where the mean would overestimate the performance of a group?

An example from the script is the math class where the mean score of 43 overestimates the performance of the class, as most students scored below 40, which is the passing percentage.

What is the mode and how is it useful in certain scenarios?

The mode is the value that occurs most frequently in a data set. It is useful in scenarios where you need to identify the most common response or the most popular item, such as in consumer surveys or inventory management.

How can the median be a better choice than the mean in certain situations?

The median can be a better choice than the mean when the data is skewed or has outliers, as it represents the middle value and is not affected by extreme data points.

What thumb rules are suggested in the video for using mean and median?

The thumb rules suggested are: use the mean when data is evenly distributed without extreme values, when all data points are important, and there are no special circumstances affecting the data. Use the median when data is skewed or has outliers.

In what type of data set can the mode be more useful than the mean or median?

The mode can be more useful in data sets with categorical variables or when you need to identify the most frequently occurring item or response, as it is not affected by extreme values.

What is a potential application of the mode in a retail setting?

A potential application of the mode in a retail setting is to determine the most popular shoe size or clothing size to stock more of, based on past sales data.

How can understanding the concepts of mean, median, and mode help in personal finance?

Understanding these concepts can help in personal finance by allowing you to analyze expenses, set budgets, and monitor spending patterns, such as using the mean to budget for monthly household expenses.

What is the importance of observing the range and distribution of data when choosing a measure of central tendency?

Observing the range and distribution of data is important because it helps determine the presence of outliers or skewness, which can influence the choice between mean, median, or mode for an accurate representation of the data.

Outlines

00:00

📊 Understanding Mean, Median, and Mode in Data Analysis

This paragraph introduces the video's focus on when and where to use mean, median, and mode in real-life scenarios. The speaker addresses the common tendency to use the mean but questions its appropriateness in all situations. A quick recap of these statistical measures is provided, with a reference to a previous video for further understanding. The importance of choosing the right measure of central tendency based on the data's distribution and presence of outliers is emphasized through examples, such as students' exam scores and food grain production data.

05:03

📈 Appropriate Use of Median and Mean in Data Summarization

This section discusses the appropriate application of median and mean in summarizing data. It uses the example of a math class's exam scores to illustrate how the mean can overestimate performance, while the median provides a more accurate representation. Similarly, the food grain production example shows how the mean can underrepresent performance due to extreme values. The speaker provides thumb rules for using mean and median, suggesting the mean is suitable for evenly distributed data without outliers, while the median is beneficial when data is skewed or has outliers.

10:05

🍦 Practical Applications of Mode in Consumer Preferences and Inventory Management

The final paragraph explores the use of mode in determining the most popular ice cream flavor through consumer research and in managing a retail shoe store's inventory. It explains how mode can identify the most frequently occurring item in a dataset, aiding in decision-making for product manufacturing and inventory stocking. The speaker also highlights that mode is particularly useful for categorical data and less applicable for continuous data without repeating values. The paragraph concludes with a tip on using mode to organize household items and a call to action for viewers to engage with the content.

Keywords

💡Summary Statistics

Summary statistics are numerical measures that summarize and describe the general features of a dataset. In the video, summary statistics like mean, median, and mode are discussed as tools to analyze data and comment on expected results. They are essential for understanding the central tendency of the data, which is a core theme of the video.

💡Mean

Mean, also known as the arithmetic average, is calculated by dividing the sum of all values in a dataset by the number of observations. The video discusses the mean as a common measure used to summarize data but also points out its limitations, such as being influenced by outliers, as seen in the example of the math class marks.

💡Median

Median is the middle value of a dataset when the observations are arranged in ascending or descending order. The video illustrates the use of the median in scenarios where the data is skewed, such as the example of the farm produce data, where the median provides a more accurate representation of the central tendency than the mean.

💡Mode

Mode refers to the value that appears most frequently in a dataset. The video explains the application of mode in situations where one is interested in the most common or popular item, such as choosing a popular ice cream flavor based on consumer preferences.

💡Skewed Data

Skewed data refers to a dataset where the distribution of values is not symmetrical and leans towards one extreme. The video uses the term to describe datasets with outliers that can distort the mean, such as the math exam scores example, where one student's exceptionally high score skews the mean.

💡Outliers

Outliers are data points that are significantly different from other observations in the dataset. The video mentions outliers as extreme values that can affect the mean, making it a less reliable measure of central tendency in certain scenarios, such as the food grain production example.

💡Categorical Data

Categorical data consists of values that are categories or groups rather than numerical values. The video discusses the use of mode with categorical data, such as the ice cream flavor preferences, where mode is a suitable measure to determine the most popular choice.

💡Continuous Data

Continuous data refers to numerical values that can take on any value within a range. The video explains that mode is less useful with continuous data, as it is difficult to find repeating values, and suggests using mean and median instead.

💡Budgeting

Budgeting in the context of the video refers to the process of estimating future expenses or production costs based on past data. The video uses the example of a soft beverage manufacturer using the mean of past sugar utilization to budget for production expenses.

💡Distribution

Distribution in statistics refers to the way values in a dataset are spread out. The video emphasizes the importance of observing the distribution of data when choosing a measure of central tendency, as evenly distributed data is more suitable for the mean, while skewed data may require the median or mode.

💡Professional and Personal Growth

The term is used by the channel 'Learning Puri' to describe its aim of providing tips and tutorials to help viewers grow in both professional and personal aspects of life. The video's content on statistical measures for data analysis contributes to this goal by teaching viewers how to make informed decisions based on data.

Highlights

Summary statistics like mean, median, and mode are often used to analyze data and comment on expected results.

People often default to using the mean, but it may not always be the most appropriate measure.

Mean is the arithmetic average of all values, useful when data is evenly distributed without outliers.

Median is the middle value in a data set and can be more representative when data is skewed.

Mode is the most frequently occurring value and is helpful for categorical data or when identifying popular items.

In a math class example, using the mean overestimates the class performance due to a skewed distribution.

For food grain production data, the mean under-represents performance due to extreme values from drought years.

Median provides a more accurate representation of central tendency in skewed data sets.

In the case of sugar utilization data for a soft beverage manufacturer, the mean is a suitable measure due to even data distribution.

Thumb rules for using mean and median are provided to help decide which measure to apply in different scenarios.

Mean can be used to study household expenses for budgeting and setting expense targets.

Mode is used to identify the most popular ice cream flavor based on consumer preferences.

A retail shoe store owner uses mode to determine the most sold shoe sizes and optimize stock.

Mode is less useful for continuous data where repeating values are less likely, unlike mean and median.

Mode can help in organizing a household by categorizing items based on frequency of use.

The video provides a comparison table for choosing between mean, median, and mode based on data characteristics.

Practical applications of mean, median, and mode are demonstrated through real-life examples for better understanding.

Transcripts

whenever we are asked to analyze data

and comment on the expected result or

the most common response we tend to find

a number that would summarize the result

we tend to use summary statistics like

mean median or mode most often people

jump at using mean or the arithmetic

average but is it the most appropriate

measure to use so what are the

applications of mean median and mode in

real-life scenarios recently I had

subscribers asking me about when and

where to use mean median and more and

that's what we are going to do in this

video so let's get rolling I have

explained the concept of mean median and

mode in this video over here you can

watch it to know the fundamentals of

mean median and mode however since the

applications of mean median and mode in

real-life scenarios were not adequately

addressed I decided to do the honors I'm

finished and you're watching my channel

learning puri where you will get tips

and tutorials to help you grow faster in

a professional and personal life so if

you're new here consider subscribing to

the channel click the Malayan to get

notified every time I post a video your

small gesture tells YouTube to push this

video to more like-minded people alright

before we proceed here is a quick recap

of what these measures of central

tendency mean mean is an arithmetic

average of all the values where we

divide the sum of all the values by the

number of observations median is the

middle value when all the observations

are lined up in an ascending or a

descending order and mode is the value

with the most number of occurrences to

get a detailed understanding of the

basics of descriptive statistics you

should watch this video over here for

which the link is posted in the

description below and infocard above I

would encourage you to watch the current

video till the end to discover some

useful tips and interesting features I

have discussed about these metrics along

the way now that is done and s-type

let's look at where we can use them

whenever we are asked to analyze data

and comment on the expected result or

the most common response

to find a number that would summarize

the result we tend to use summary

statistics like mean median or mode most

of the people jump at using mean or the

arithmetic average but is it the most

appropriate measure to use let's look at

this example in a math class the marks

obtained by 13 students during the exam

are as follows the teacher wanted to

know how the class was faring overall

the immediate tendency is to take a mean

or an arithmetic average of the marks

obtained by students in this case it

will be forty three point one for

approximately four three this is

obtained by dividing 3:02 which is the

sum of all the box divided by the number

of students obviously all except one

student have scored below 40 which is

the passing percentage and they seem to

be having a tough time in the class if

the teacher used this average of 43 to

describe the performance of the class

then she would be overestimating the

performance of the class on the higher

side based on how the class actually

performed this clear it cannot be true

right in this data set

there is one number that is 99 which is

polarized to one extreme here the data

is described as not evenly distributed

or skewed now let's take another example

the government was studying food grain

output of one state in a country across

seven years from 1969 to 1975 the output

measured in metric tonnes is in this

table across seven years from 1969 to

1975 if we summarize the performance for

this data set using mean then we would

have thirty three point five metric tons

of average food grade production across

the seven years like usual this average

is obtained by dividing two 34.5 the sum

of production across seven years by

seven using this average figure the

performance for five years appears above

average barring the two years that is

1971 and 1972 where it is below average

this again under represents the

performance in both these cases we

discussed we observed two peculiar

features in the data first the data is

skewed to one end that is there are

extreme values or outliers

the data and second the arithmetic

average assigns equal weight edge to

each data point in the data set that is

we divide each data point in both the

data sets by seven which is the number

of observations however here's the

caveat in the first example of marks in

the math exam we have data set that is

polarized or skewed to one end in the

second data set of food grain production

years 1971 and 1972 were two years that

the state faced an extreme drought

resulting in lower produced both these

two cases have Extra Ordinary scenarios

in the second case the data is not only

skewed but also equal importance is

being given to two years of drought

against five years of good rainfall

during the comparison it's like

comparing apples to oranges now let's

look at doing something different for

the math exam performance if the teacher

wanted to summarize the performance she

could use the median when we use the

median we get thirty five as a middle

figure for the class performance there

are exactly 50% of students above and

below this figure hmm this seems to work

for the farm produced data using median

45 works out to be the middle figure 45

provides an acceptable average

production across years despite the two

years of drought so there are instances

when not jumping at taking the

arithmetic average or the mean is

actually beneficial now that we are

aware when not to jump at using the

arithmetic average here is one more

example let's say you're working for a

manufacturer of soft beverage like Pepsi

or coke who uses refined sugar in the

manufacturing process seven months of

data of sugar utilization in their

factory is laid out in this table and

now you are tasked to budget for likely

production expenses in the year to come

so with our newfound understanding let's

work it out we observe that unlike the

early to cases the data is not skewed to

one or any end the data is evenly spread

or distributed across the seven months

that means that there are no extreme

values to deal with in this data set the

arithmetic average of this data set

comes to 2 1 9 metric tons obtained by

dividing 1/5 free--free in the sum of

the data by 7 on a simple comparison

with the data set this value appears to

be very acceptable the company can

safely use this figure of 2 benign

metric tons as an average sugar

utilization for manufacturing in

budgeting for their production expenses

to help you figure out when to use mean

and median I have summarized a few thumb

rules for using mean and median over

here in this table we can safely

conclude that we can use the arithmetic

average or mean to summarize our data in

the following instances first when we

have evenly distributed data that is the

data is not skewed or does not have

extreme values second when we need to

use all the data available and thirdly

there are no special circumstances like

the drought and agricultural produce

affecting the importance given to each

data point and in case if you are

violating the conditions 1 & 2 we can

consider using the medium as promised

here is a quick tip do you know we can

use the mean to study expenses like food

and electricity consumption in the

household to budget for expenses every

month this way you can monitor and set

expense targets to plan for your savings

before we move on to discussing the

application for mode if you have found

value in this information so far please

like and share the video with your

friends and acquaintances this motivates

me to create more good content for you

on the other hand it makes you look cool

when you help your friends to improve

their understanding I know yes the

manufacturer of the soft beverage

company is reminding you to subscribe to

this channel and click on the bell icon

to get notified every time a video is

posted on this channel now in this next

example we have a manufacturer of ice

cream who wants to choose a popular

flavor of ice cream for manufacturing he

employed a consumer research firm and

conducted a survey of hundred people

they were asked to choose the most light

flavor from amongst four flavors of ice

cream the choice given to the consumers

worth shop

vanilla strawberry and peach so how do

you choose the flavor that would most

appeal to a group of people well from

this data it's a no-brainer

that many people chose the chocolate

flavor so when we choose the most common

response or the most frequently

occurring response we are using the mode

did you find this amazingly simple then

here's one more case a retail shoe store

owner has observed that every month he

has many shoe sizes that are not sold at

all or stay in the stock for a long time

he often must carry out an unseasonal

sale offer to clear the stocks

maintaining a long-standing stock or

dead stock has become commercially

unviable for him he had observed that

sales for each shoe size were fairly

consistent across each month so he

decided to take the average of past 12

months he undertook a statistical

analysis of various shoe sizes sold by

him and created the following table the

table depicts the average monthly sales

in number of shoes sold for each shoe

size the analysis indicated to him that

size is 6 7 & 8 are the most sold sizes

these where the modes of the data set we

can therefore see that we can have more

than one mode in a data set here's

something interesting using the

frequency of the sold items we observe

that even size 10 is sold in

sufficiently large numbers therefore we

can advise the retail shoe store manager

to even stock size 10 mode is a useful

measure in case we wanted to decide on

more than one summary item not just that

it can also help you choose when you

have data on a categorical variable like

the one we saw in the case of ice cream

flavor preferred like the median mode

does not get affected by extreme values

however when you have continuous values

like one twenty two point two thirty

four point five thirty seven point nine

and so on there is less likelihood of

obtaining a repeating value and finding

a mode is either difficult or impossible

mode is a useless measure in such

instances therefore continuous values

are best

my mean and median as against mood so

here's the comparison table updated for

mood you can look up this video on basic

statistics to gain an understanding on

categorical and continuous data the link

for this is posted in the description

below as well as in the info card above

so all right here's an important tip so

next time you're confused on which

measure of central tendency or average

to use first consider observing the

range and the distribution of the data

this will give you a far better

understanding combining with the thumb

rules in the comparison table I have

shared with you to decide which measure

of average to apply in a real life

scenario before I share another quick

tip with you if you have not yet

subscribed do consider subscribing and

if you did find value in this video so

far don't forget to like and share the

video with your friends and

acquaintances all your gestures motivate

me to keep on churning out more good

content for you so as promised here is

another quick tip do you know you can

categorize the items and tools use in

your household based on mood to help you

organize the household the most used

items can stay in the most reachable

places as against the less used items

similarly you can even clear the

household of unused and less used items

by selling them off and replacing them

with something more useful this will

help you clear an awful amount of

clutter in your house so leave a less in

the comment below if you have used more

to help you organize your household also

do let me know in the comments below by

tidying yes if you have used mode in any

other place other than your profession

and yes where have you used it to know

more about how data is collected you

could watch this video over here thanks

for watching see you in the next video

till the next time stay healthy and stay

peaceful