11th Grade Mathematics
Summary
TLDREn este video, un maestro guía a sus estudiantes en la creación de un gráfico de dispersión utilizando datos históricos del tiempo ganador en los 100 metros masculinos de los Juegos Olímpicos entre 1900 y 1996. A través de un ejercicio interactivo, los estudiantes predicen el coeficiente de correlación y analizan la relación entre las fechas y los tiempos de las victorias. También exploran cómo utilizar la regresión lineal para predecir futuros resultados olímpicos, como el tiempo de la carrera en los Juegos Olímpicos de 2020. Finalmente, se discute el impacto de estos datos en diversas profesiones, desde el análisis deportivo hasta la industria de la salud.
Takeaways
- 📊 La clase utiliza el ejemplo de Michael Phelps para introducir el análisis de datos y predicciones deportivas.
- 📈 Los estudiantes trabajan con datos históricos del tiempo ganador en los 100 metros planos entre 1900 y 1996.
- 🧠 Se pide a los alumnos pensar de manera independiente antes de colaborar en grupos para diseñar una gráfica de dispersión.
- 🪧 Cada grupo debe decidir sus propios ejes, escalas, etiquetas y si necesitan usar un ‘break’ en los ejes.
- 📉 Los estudiantes identifican que la relación entre año y tiempo ganador es lineal y con pendiente negativa.
- 🔎 Aprenden a estimar el coeficiente de correlación observando qué tan cerca están los puntos de una línea recta.
- 🧮 Usan calculadoras para ingresar los datos, generar el diagrama de dispersión y calcular la regresión lineal y el coeficiente real.
- 🥇 Los estudiantes comparan sus estimaciones de correlación con el valor exacto y celebran al grupo que se acerque más.
- 🔮 La clase utiliza la ecuación de regresión para predecir tiempos futuros, como los de 2012 y 2020, comprobando cercanía con resultados reales.
- 🚀 Se discute cómo diversas profesiones (atletas, entrenadores, apuestas, salud, marcas deportivas, periodistas) pueden usar estas predicciones.
- 📉 La maestra guía una reflexión sobre el límite físico del rendimiento humano y cómo eventualmente la tendencia deberá estabilizarse.
- 🏁 Como actividad final, cada estudiante predice el tiempo necesario para ganar oro en 2016 y explica su razonamiento.
Q & A
¿Quién es Michael Phelps y por qué es famoso?
-Michael Phelps es un nadador estadounidense famoso por ganar ocho medallas de oro en los Juegos Olímpicos de Beijing y por tener el récord mundial de más medallas olímpicas de todos los tiempos.
¿Qué deben saber los estudiantes sobre Michael Phelps si están entrenando para las Olimpiadas de 2016?
-Los estudiantes deberían saber la velocidad promedio a la que nada Michael Phelps para poder predecir su rendimiento y entrenar para superarlo en una competencia.
¿Cómo se relaciona el tema de Michael Phelps con la actividad matemática de la clase?
-La actividad matemática consiste en analizar los tiempos ganadores en los 100 metros planos de los Juegos Olímpicos desde 1900 hasta 1996. Los estudiantes deben graficar estos datos y calcular el coeficiente de correlación, similar a cómo se predicen los tiempos de Phelps en las Olimpiadas.
¿Qué tipo de gráfico se espera que los estudiantes construyan en la actividad?
-Los estudiantes deben crear un gráfico de dispersión (scatter plot) con el año olímpico en el eje X y el tiempo ganador de los 100 metros en el eje Y.
¿Qué es un coeficiente de correlación y cómo se calcula en esta actividad?
-El coeficiente de correlación mide la relación entre dos variables. En esta actividad, los estudiantes calculan el coeficiente de correlación para su gráfico de dispersión, estimando su valor antes de usar la calculadora para obtenerlo con mayor precisión.
¿Por qué se usa un 'break' (quiebre) en el gráfico y cómo debe ser implementado?
-El 'break' se usa en el eje Y para representar el intervalo de los tiempos de forma más clara y adecuada. Se coloca en la parte inferior del gráfico cuando los datos no comienzan desde cero, permitiendo una mejor visualización.
¿Cómo puede el gráfico de dispersión ayudar a predecir el futuro?
-El gráfico de dispersión puede ayudar a predecir futuros tiempos ganadores, ya que permite observar la tendencia de los tiempos a lo largo de los años. Al aplicar una regresión lineal, se puede estimar el tiempo de la próxima competencia.
¿Qué factores pueden afectar la exactitud de las predicciones basadas en estos gráficos?
-Los factores que pueden afectar la exactitud de las predicciones incluyen cambios en el rendimiento de los atletas, la evolución de las técnicas de entrenamiento, y la mejora de la tecnología en el deporte, como las zapatillas deportivas.
¿Qué es una 'outlier' (valor atípico) y cómo se identifica en el gráfico?
-Un 'outlier' es un punto de datos que está significativamente alejado de la tendencia general del gráfico. En este caso, es un tiempo de carrera que no sigue el patrón de los otros, y se identifica visualmente como un punto aislado.
¿Cuál es la importancia de los coeficientes negativos en la regresión lineal de este tipo de actividad?
-Un coeficiente negativo indica que hay una relación inversa entre las dos variables, lo que en este caso significa que a medida que los años avanzan, el tiempo en el que se corre la prueba de 100 metros disminuye, es decir, los atletas se vuelven más rápidos con el tiempo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
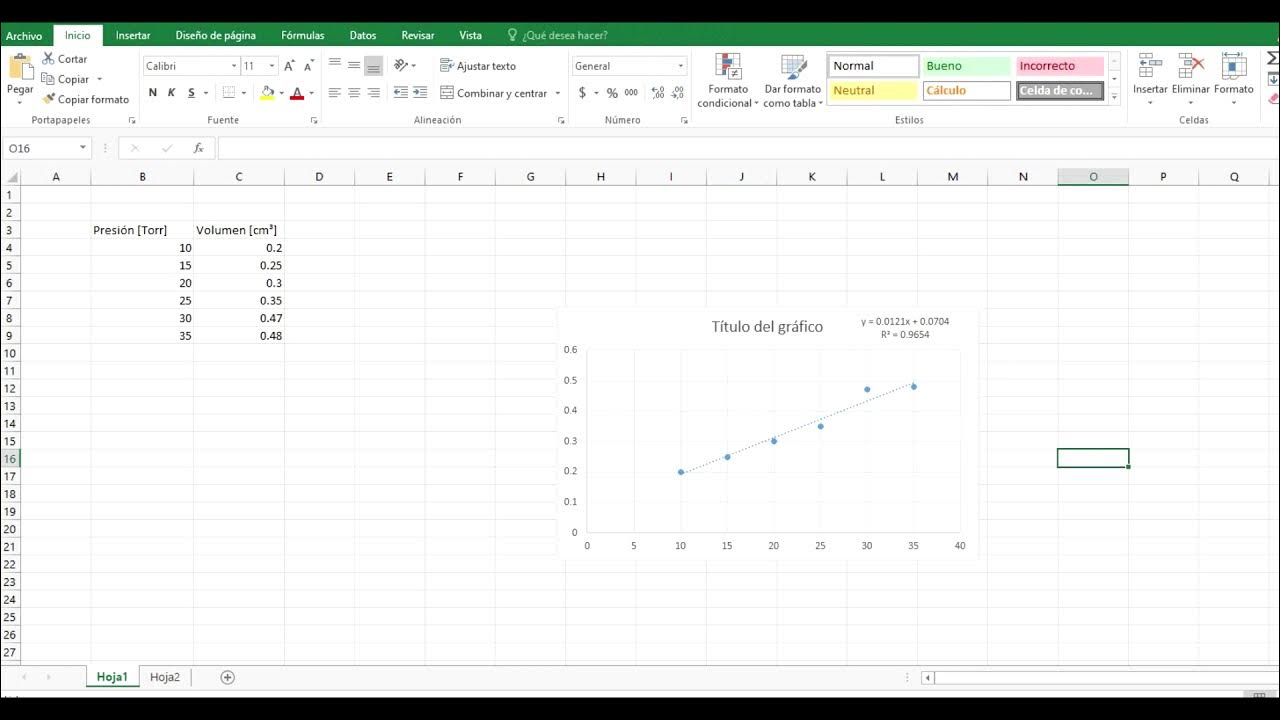
COMO AGREGAR LÍNEA DE TENDENCIA Y ECUACIÓN EN EXCEL | LORENA GARCÍA

Medida de Dispersión en los resultado de una prueba-Resolución ficha 9 libro matemática 5to grado

🥇🥈 ORIGEN, HISTORIA Y CURIOSIDADES DE LOS JUEGOS OLÍMPICOS 🥉💪🏼

Historia del Ciclismo | El Deporte sobre Ruedas | El Ciclismo en Ruta

Conociendo los Juegos Olímpicos - Reglamento e historia - Material educativo
Diagrama de Dispersión en Excel
5.0 / 5 (0 votes)
