Draw Parabola Grade 11 | Part 1 | Grade 11 Functions
Summary
TLDRThis video introduces grade 11 students to parabolas, exploring how changes in their equations affect their graphs. Key concepts include recognizing parabolas, vertical and horizontal shifts, and the impact of positive and negative values on the graph’s orientation. The video explains how to determine whether a parabola is 'happy' or 'sad,' and demonstrates methods to sketch graphs, focusing on translating parabolas and finding turning points. It also covers how to use the quadratic formula and turning point form for precise graphing, offering students a clear guide to graph transformations and sketching techniques.
Takeaways
- 😀 Parabolas are defined by equations of the form y = x², with the key feature being the x² term, distinguishing them from exponential graphs.
- 😀 Exponential graphs have x in the exponent, while parabolas have x as the base (x²).
- 😀 A parabola's graph can be shifted vertically by adding or subtracting a constant to the equation (e.g., y = x² + 1 shifts it upwards).
- 😀 Horizontal shifts in parabolas are made by modifying the x value inside parentheses (e.g., x - 2 shifts the graph 2 units to the right).
- 😀 When shifting horizontally, the direction is opposite to the sign: 'minus' moves the graph right, and 'plus' moves it left.
- 😀 The 'a' value in the equation y = a(x - h)² + k determines whether the parabola is 'happy' (positive a) or 'sad' (negative a).
- 😀 A larger 'a' value makes the parabola narrower, while a smaller 'a' value makes it wider. However, the exact value of 'a' is less important for basic graphing.
- 😀 Practice with parabolas focuses on understanding vertical and horizontal shifts, and whether the graph is 'happy' or 'sad', without needing precise x- or y-intercepts.
- 😀 Example problems involve determining the direction and movement of the graph based on equation parameters, such as shifts and the sign of 'a'.
- 😀 For sketching parabolas, key steps include finding the x-intercept (set y = 0), the y-intercept (set x = 0), and the turning point using various methods like the quadratic formula.
Q & A
What is the basic shape of a parabola, and what is its general equation?
-A parabola is a U-shaped curve that can open either upwards or downwards. The general equation for a parabola is y = x², where the x is squared, and the graph's turning point is at (0, 0).
How do you differentiate between a parabola and an exponential graph?
-The main difference is that for a parabola, the x is squared (e.g., y = x²), whereas for an exponential graph, the x is in the exponent (e.g., y = 2^x).
How does a '+1' in the equation y = x² + 1 affect the graph?
-The '+1' in the equation y = x² + 1 shifts the parabola one unit upwards, changing the turning point from (0, 0) to (0, 1).
What does placing the x-value inside brackets (e.g., y = (x - 2)²) do to the graph?
-Placing the x-value inside brackets shifts the graph horizontally. In this case, the equation y = (x - 2)² moves the parabola 2 units to the right.
Why is it important to remember that horizontal shifts are in opposites?
-Horizontal shifts follow the rule that 'minus' shifts the graph to the right, and 'plus' shifts the graph to the left. This is opposite to the intuitive understanding, so it's essential to apply the opposite logic for horizontal shifts.
How does the coefficient in front of x² (the 'a' value) affect the shape of the parabola?
-The 'a' value determines whether the parabola opens upwards or downwards. If 'a' is positive, the parabola is 'happy' (smiles), and if 'a' is negative, the parabola is 'sad' (frowns). Additionally, a larger value of 'a' makes the parabola narrower, while a smaller value makes it wider.
What happens to the parabola if the 'a' value is negative?
-If the 'a' value is negative, the parabola opens downwards, creating a 'sad' shape. The larger the absolute value of 'a', the steeper and narrower the parabola.
What does a horizontal shift of x - 1 mean in terms of the parabola's movement?
-The equation x - 1 means the parabola shifts 1 unit to the right. Remember that a negative sign inside the brackets corresponds to a shift to the right.
In the equation y = x² - 7x - 5, how would you find the x-intercepts?
-To find the x-intercepts, set y = 0 and solve the equation x² - 7x - 5 = 0. You can factorize the equation or use the quadratic formula to find the x-intercepts.
What is the turning point of a parabola, and how do you find it from the equation?
-The turning point is the vertex of the parabola, which can be found by using the x-coordinate formula x = -b/2a, where 'a' and 'b' come from the quadratic equation y = ax² + bx + c. Once you find the x-coordinate, substitute it back into the equation to get the y-coordinate of the turning point.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
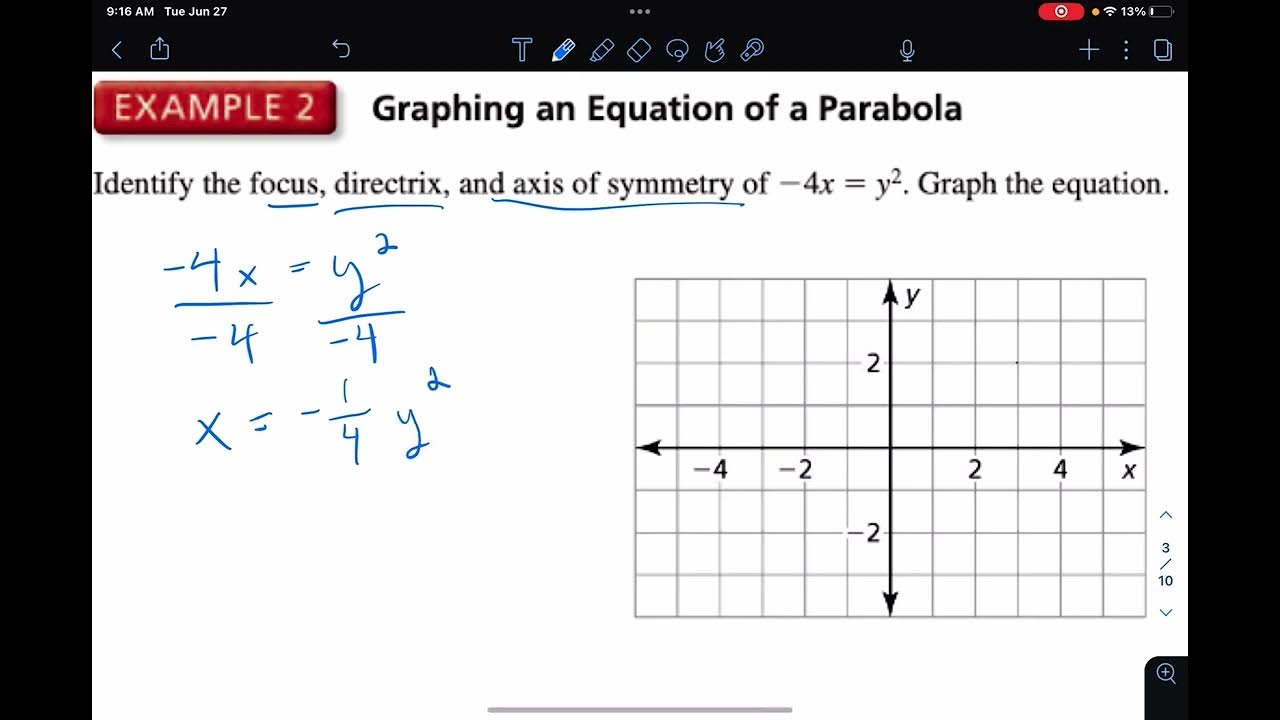
A2 Focus and Directrix

Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV) dengan Metode Grafik.

SHS General Mathematics Q1 Ep1: Function

EPISODE 1- GENERAL MATHEMATICS : Answering Sample Questions in Modules
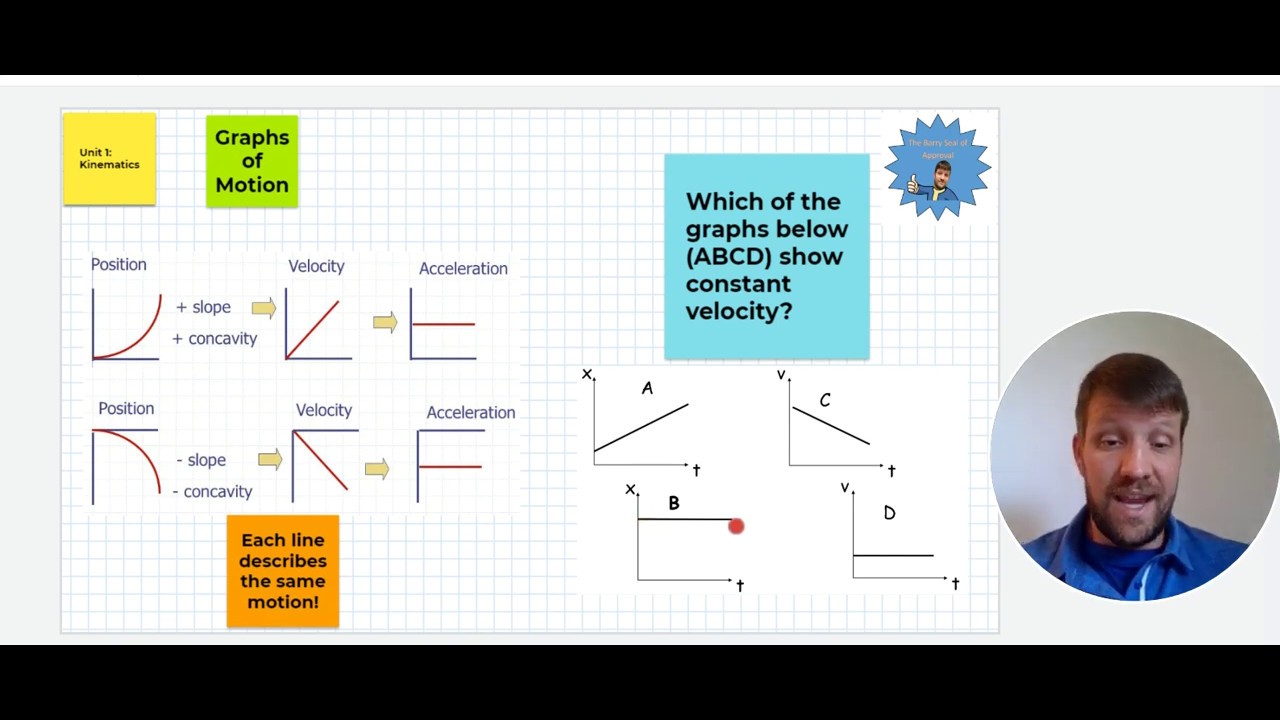
AP Physics 1 - Unit 1 Summary - Kinematics

Conic Sections (Parabola, Ellipse & Hyperbola) All Important Formulas & Tricks for JEE Mains 2023
5.0 / 5 (0 votes)