Limit Fungsi Aljabar • Part 4: Bentuk Tak Tentu dan Sifat-Sifat Limit Fungsi

Summary

In this video, the concept of limits in algebraic functions is explored, focusing on indeterminate forms and the properties of limits. The video explains the various indeterminate forms, such as 0/0 and infinity/infinity, and distinguishes them from undefined results. It further delves into the properties of limits, including how limits interact with constants, functions' sum, difference, product, quotient, exponentiation, and logarithms. The video aims to provide viewers with a comprehensive understanding of these fundamental mathematical concepts, useful for solving limit problems in algebraic functions.

Takeaways

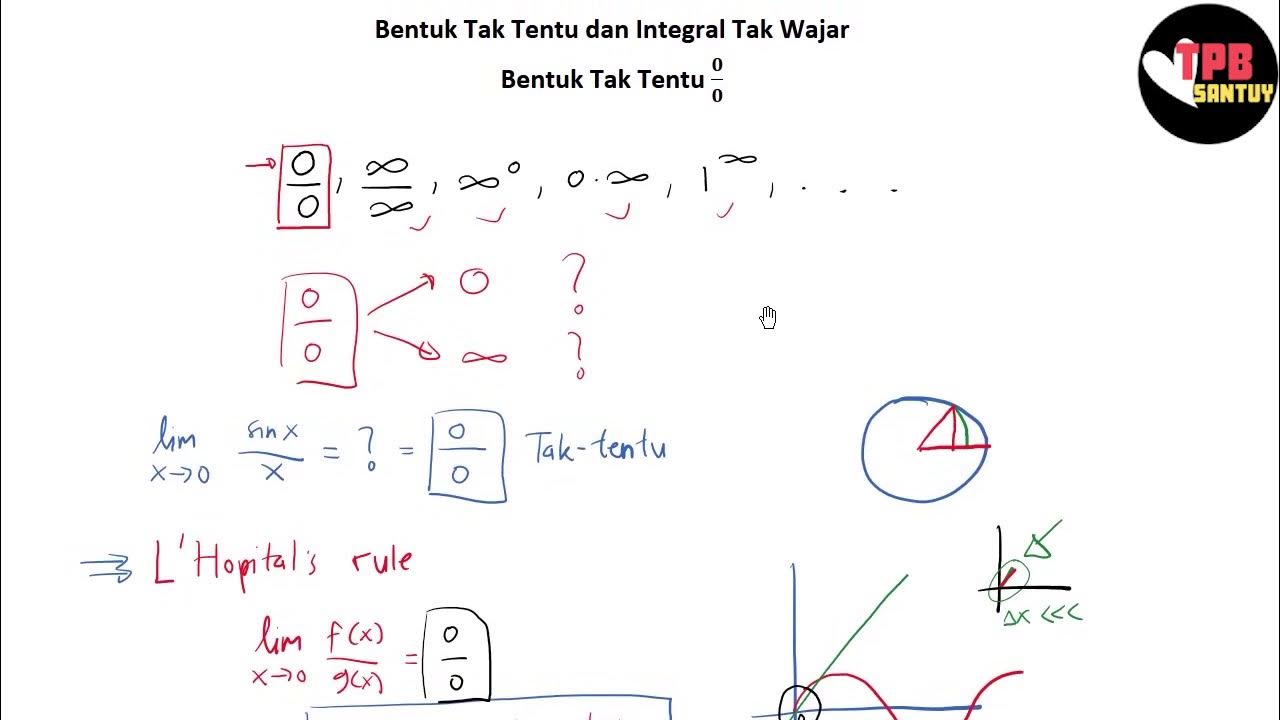
• 😀 Indeterminate forms occur when the result of solving a limit function is undefined or has multiple possible outcomes.
• 😀 One of the most common indeterminate forms is 0/0, where the result can vary depending on the situation, making it indeterminate.
• 😀 Other examples of indeterminate forms include infinity/infinity, 0 raised to a finite power, and 1 raised to the power of 0.
• 😀 It's important to differentiate between undefined expressions (such as division by zero) and indeterminate forms, which can have multiple solutions.
• 😀 Indeterminate forms can have different values depending on the context and must be processed further to determine a concrete limit value.
• 😀 In contrast to indeterminate forms, undefined expressions (like dividing by zero) have no solution and are considered undefined.
• 😀 The first property of limits is that if a function approaches a constant value, the limit will be that constant.
• 😀 Limits can be applied to various operations, including addition, subtraction, multiplication, division, exponentiation, roots, and logarithms.
• 😀 The limit of a quotient of two functions can be calculated, provided the denominator is not zero, as division by zero is undefined.
• 😀 Constants can be factored out of a limit operation, and the result of the limit of the constant function is simply the constant itself.

Q & A

What is an indeterminate form in limits?

An indeterminate form is a result obtained when solving a limit that does not give a definitive answer. For example, 0/0 is an indeterminate form, meaning the limit may yield multiple possible outcomes depending on the context.

What are the seven types of indeterminate forms?

The seven types of indeterminate forms are: 0/0, ∞/∞, 0^0, ∞^0, 1^∞, 0*∞, and ∞-∞.

How do indeterminate forms differ from undefined expressions?

Indeterminate forms, like 0/0, have multiple possible outcomes depending on how the limit is processed. In contrast, undefined expressions like dividing by zero (e.g., 1/0) do not result in any meaningful value and are considered undefined.

Why is 0/0 considered an indeterminate form?

0/0 is considered an indeterminate form because it can yield different results based on the specific functions involved. For example, depending on the limits of the numerator and denominator, it could approach 0, 1, or other values.

What is the significance of the limit properties discussed in the video?

The properties of limits allow us to manipulate and solve limits of functions by applying basic mathematical operations, such as addition, subtraction, multiplication, division, exponentiation, and logarithms, within the limit expression.

Can limits be applied to all mathematical operations?

Yes, limits can be applied to operations such as addition, subtraction, multiplication, division, exponentiation, and logarithms, as long as the conditions are met (e.g., no division by zero).

What is the role of constants in the properties of limits?

In the properties of limits, constants can be factored out of the limit. For example, the limit of a constant multiplied by a function is the constant multiplied by the limit of the function.

What happens when the denominator approaches zero in a limit?

If the denominator of a fraction approaches zero, the limit might not exist unless the numerator also approaches zero in a specific way. In cases where the denominator approaches zero and the numerator is non-zero, the limit may tend towards infinity.

How does the property of limits apply to functions with exponents?

The property of limits allows exponents to be applied to the limit of a function. For example, the nth power of a limit can be calculated by first evaluating the limit of the function and then raising it to the nth power.

What does it mean when a limit results in an indeterminate form like 0^0?

A limit resulting in 0^0 is an indeterminate form because, depending on the specific function, the limit can approach different values. This requires further techniques, such as L'Hopital's Rule or rewriting the expression, to resolve.