Ecuaciones Diferenciales de primer orden - Aplicaciones - Periodo Medio - Desintegración
Summary
TLDREn este video se explica la aplicación de las ecuaciones diferenciales de primer orden en el contexto de la desintegración radiactiva. Se aborda cómo la media vida o período de una sustancia radiactiva mide su estabilidad, y cómo calcular el tiempo necesario para que una cantidad determinada se desintegre. Se presentan dos ejemplos prácticos: uno sobre la desintegración de un isótopo de plomo, y otro sobre el cálculo del período medio de un isótopo de plutonio. El video resalta la importancia de entender el modelo exponencial de desintegración y su aplicación en situaciones reales de física y matemáticas.
Takeaways
- 😀 La ecuación diferencial de primer orden es fundamental para modelar fenómenos de desintegración radiactiva y crecimiento poblacional.
- 😀 El período medio es una medida de la estabilidad de una sustancia radiactiva y mide el tiempo que tarda la mitad de los átomos de una muestra en desintegrarse.
- 😀 La desintegración radiactiva sigue un modelo exponencial en el que la cantidad de sustancia disminuye a una tasa proporcional a la cantidad presente.
- 😀 Ejemplo 1: Para el plomo-109, con una vida media de 3.3 horas, se calcula cuánto tiempo pasa hasta que el 90% se desintegra, utilizando la ecuación de decaimiento.
- 😀 La fórmula para la desintegración radiactiva es n(t) = n₀ * e^(kt), donde n(t) es la cantidad de sustancia en el tiempo t y k es la constante de desintegración.
- 😀 Para encontrar la constante de desintegración, se usa el valor de n en un tiempo dado, aplicando logaritmos naturales a ambos lados de la ecuación.
- 😀 Ejemplo 2: En el caso del uranio-238, después de 15 años de decaimiento, el 0.043% de la muestra original se ha desintegrado, y se usa esta información para calcular el período medio de plutonio-239.
- 😀 La fórmula para calcular el período medio (tiempo que tarda en reducirse a la mitad) es similar a la de la desintegración, utilizando logaritmos para despejar el tiempo.
- 😀 El período medio de una sustancia radiactiva puede ser extremadamente largo, como el caso del plutonio-239, que tiene un período medio de 24,180 años.
- 😀 Los residuos radiactivos, como los generados en plantas nucleares, pueden tardar miles de años en desintegrarse, por lo que se almacenan de manera segura hasta que se desintegren completamente.
- 😀 El concepto de desintegración radiactiva se aplica no solo a la física nuclear, sino también a otros campos que involucran procesos de decaimiento o disminución exponencial.
Q & A
¿Qué es el período medio de una sustancia radiactiva?
-El período medio es una medida de la estabilidad de una sustancia radiactiva, indicando el tiempo que tarda en desintegrarse la mitad de los átomos de una muestra inicial.
¿Qué ocurre con los átomos de radio después de 1700 años?
-Después de 1700 años, la mitad de los átomos de radio se desintegran, convirtiéndose en radón-222.
¿Cuánto tiempo tarda el Uranio-238 en convertirse en Plutonio-239?
-El Uranio-238 tiene un período medio de 4.5 mil millones de años para convertirse en Plutonio-239.
¿Cómo se resuelve un problema de desintegración radiactiva utilizando ecuaciones diferenciales de primer orden?
-Se resuelve con la ecuación diferencial n'(t) = -k * n(t), donde n(t) es la cantidad de sustancia en el tiempo t y k es la constante de desintegración. La solución general es n(t) = n_0 * e^(-kt), donde n_0 es la cantidad inicial.
¿Cómo se encuentra la constante de desintegración 'k' en estos problemas?
-La constante de desintegración 'k' se encuentra utilizando el valor de la mitad de la vida (tiempo en el que se reduce a la mitad la cantidad de sustancia) y la fórmula k = ln(0.5) / t_half.
En el ejemplo de Pb-109, ¿cuánto tiempo debe transcurrir para que el 90% de la sustancia se desintegre?
-En el caso de Pb-109, para que se desintegre el 90%, es necesario que transcurran aproximadamente 10.96 horas.
¿Qué significa que la tasa de desintegración de una sustancia sea proporcional a la cantidad presente?
-Significa que la cantidad de sustancia que se desintegra en un tiempo dado es proporcional a la cantidad restante de la sustancia en ese momento.
En el caso del Uranio-238, ¿qué cantidad de plutonio-239 queda después de 15 años si solo el 0.043% se desintegra?
-Después de 15 años, queda el 99.9957% de la cantidad inicial de plutonio-239.
¿Cómo se calcula el período medio de un isótopo radiactivo en el caso de plutonio-239?
-Para calcular el período medio de plutonio-239, se usa la ecuación de desintegración y se resuelve para el tiempo necesario para que la sustancia se reduzca a la mitad. En este caso, el período medio es aproximadamente 24,180 años.
¿Por qué es importante saber el período medio de una sustancia radiactiva?
-Es importante porque nos ayuda a entender cuánto tiempo tomará para que una sustancia radiactiva se desintegre y sea menos peligrosa, lo que es crucial en aplicaciones como la gestión de residuos nucleares.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Orden de una Ecuación Diferencial

Variables Separables, video 1

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED
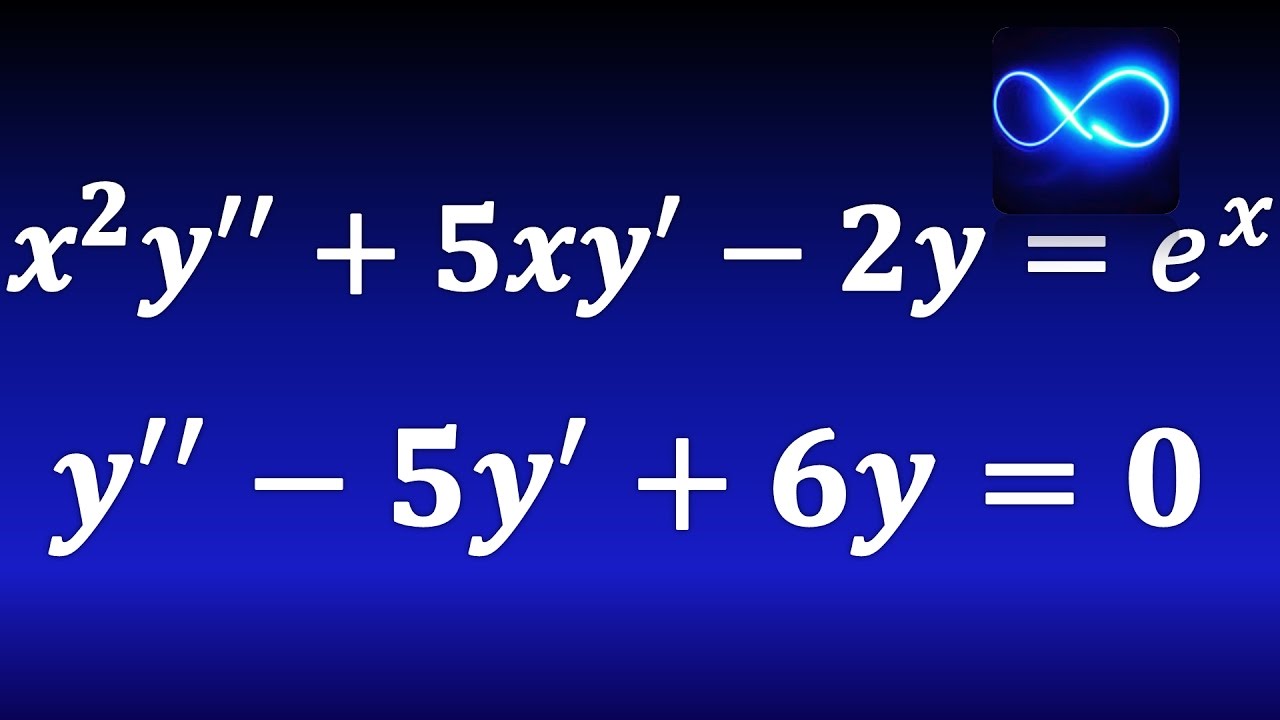
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
Ecuaciones diferenciales con Mathematica: Apliaciones de los sistemas de ecuaciones diferen | | UPV

79. Funciones linealmente independientes ¿qué son? CON EJEMPLOS
5.0 / 5 (0 votes)
