Volumen de sólidos compuestos
Summary
TLDREn este video, el profesor Roberto explica cómo calcular el volumen de sólidos compuestos, descomponiéndolos en figuras geométricas conocidas como un cono y una esfera. A través de ejemplos prácticos, enseña a calcular el volumen de un hemisferio y un cono, utilizando las fórmulas correspondientes. Además, se presentan ejemplos de sólidos combinados, como un cilindro y un cono, y se proporcionan ejercicios para que los estudiantes apliquen los conceptos aprendidos. El enfoque es sencillo, favoreciendo la comprensión de los estudiantes y asegurando su éxito en el cálculo de volúmenes de sólidos compuestos.
Takeaways
- 😀 El volumen de sólidos compuestos se puede calcular descomponiéndolos en cuerpos geométricos conocidos, como el cono y la esfera.
- 😀 El volumen de una esfera es la mitad de la fórmula del volumen de una esfera completa: (4/3)πr³ dividido entre 2.
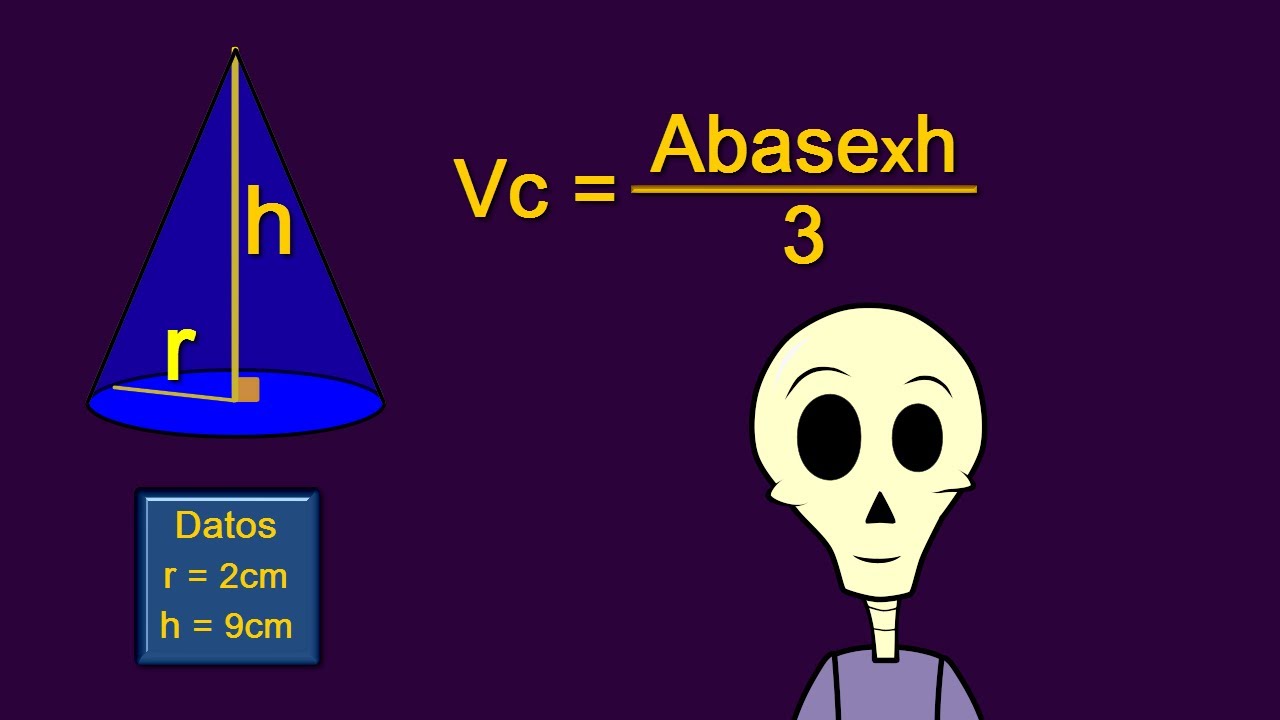
- 😀 Para calcular el volumen de un cono, se usa la fórmula (1/3)πr²h, donde r es el radio y h es la altura del cono.
- 😀 En un ejemplo, se calculó el volumen de una figura compuesta por un hemisferio (radio de 5 cm) y un cono (radio de 5 cm, altura de 2 cm), resultando en 183.3 cm³.
- 😀 Para calcular el volumen de un hemisferio, se usa la fórmula (1/2) * (4/3)πr³, donde r es el radio del hemisferio.
- 😀 En otro ejemplo, se mostró cómo calcular el volumen de un cono con radio de 3 cm y altura de 7 cm, utilizando la fórmula correspondiente.
- 😀 También se mostró cómo calcular el volumen de una figura compuesta por un cilindro (radio 6 cm, altura 8 cm) y un cono (radio 6 cm, altura 4 cm), sumando los volúmenes de ambos cuerpos.
- 😀 Se debe identificar siempre los valores de los radios y las alturas de las figuras al calcular sus volúmenes.
- 😀 Un ejercicio final requiere calcular el volumen de un cilindro y un hemisferio, donde ambos tienen un radio de 3 cm y el cilindro tiene una altura de 6 cm.
- 😀 Es importante practicar con diferentes combinaciones de cuerpos geométricos compuestos para entender mejor los cálculos de volúmenes y asegurarse de usar las fórmulas correctas.
Q & A
¿Cuál es el objetivo principal de la clase 3.1?
-El objetivo principal de la clase 3.1 es enseñar a calcular el volumen de sólidos compuestos, utilizando figuras geométricas conocidas como el cono y la esfera hemisférica.
¿Cómo se calcula el volumen de un hemisferio según la clase?
-El volumen del hemisferio se calcula tomando la mitad del volumen de una esfera, que se obtiene con la fórmula (4/3)πr³, y luego se divide entre dos, resultando en (2/3)πr³.
¿Qué fórmula se utiliza para calcular el volumen de un cono?
-La fórmula para calcular el volumen de un cono es (1/3)πr²h, donde r es el radio y h es la altura del cono.
¿Cómo se resuelve el volumen de un sólido compuesto?
-Para resolver el volumen de un sólido compuesto, se descompone en cuerpos geométricos conocidos, como un cono y un hemisferio, y se suman los volúmenes de estos cuerpos.
¿Cuánto es el volumen de un hemisferio con radio de 5 cm?
-El volumen del hemisferio con radio de 5 cm es de aproximadamente 83.3 cm³, calculado usando la fórmula (2/3)π(5)³.
¿Qué valores se necesitan para calcular el volumen de un sólido compuesto con un cono y un hemisferio?
-Se necesitan el radio y la altura del cono y el radio del hemisferio. Por ejemplo, si el radio es 5 cm y la altura del cono es 2 cm, se usan estas medidas para calcular los volúmenes por separado.
Si el radio de un hemisferio es 3 cm, ¿cómo se calcula su volumen?
-Para un hemisferio con radio de 3 cm, su volumen se calcula como (1/2) × (4/3)π(3)³, lo que da aproximadamente 56.55 cm³.
¿Cómo se calcula el volumen de un cilindro y un cono con el mismo radio?
-Para un cilindro, se utiliza la fórmula πr²h, y para un cono, se usa (1/3)πr²h. En ambos casos, el radio es el mismo, pero sus alturas son diferentes, lo que afecta el resultado.
¿Cómo se calculan los volúmenes de un cilindro y un cono con radio 6 cm y alturas 8 cm y 4 cm, respectivamente?
-El volumen del cilindro es π(6)²(8) = 904.32 cm³, y el volumen del cono es (1/3)π(6)²(4) = 226.195 cm³.
¿Cuál es el volumen total de un sólido compuesto por un cilindro y un cono con las medidas mencionadas?
-El volumen total del sólido compuesto sería la suma de los volúmenes del cilindro y el cono, es decir, 904.32 cm³ + 226.195 cm³ = 1130.515 cm³.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)