A-Level Maths: E6-01 Compound Angles: Proving the Compound Angle Formulae
Summary
TLDRIn this video, the presenter demonstrates a geometrical proof for the compound angle formula, explaining that angles x, y, and x+y are all acute for the proof to work. The proof involves a series of geometric steps using trigonometric identities, including sine and cosine values. By constructing triangles and applying trigonometric relationships, the formula for sine and cosine of compound angles is derived. The presenter also explores the formula for tan(a + b), showing how the division by cos(a)cos(b) results in the compound angle formula for tangent, while ensuring the correctness of the signs based on the assumption of acute angles.
Takeaways
- 😀 Angles x, y, and x + y are all assumed to be acute for the geometrical proof to work.
- 😀 The geometrical proof begins with a rectangle and a right-angled triangle, where one side is given a length of 1.
- 😀 Using basic angle relationships (90° - x and 90° - y), the script demonstrates how to find various internal angles.
- 😀 The sum of the three interior angles (90° + 90° - x) adds up to 180°, leading to an angle of x.
- 😀 Parallel lines and alternate angle theory are applied to conclude that one angle is x + y.
- 😀 Using trigonometric functions, the lengths of different sides are determined, such as sine x * cos y for one side.
- 😀 The proof derives key side lengths, including cos x * cos y and sine x * sine y, using trigonometric identities.
- 😀 A reflection principle is explained, with cosine remaining unchanged under reflection in the y-axis, while sine changes sign under reflection in the x-axis.
- 😀 The proof concludes that sine of (x + y) equals sine x * cos y + cos x * sine y, and cosine of (x + y) equals cos x * cos y - sine x * sine y.
- 😀 The compound angle formula is extended to sine and cosine for both addition and subtraction of angles.
- 😀 The tangent formula for compound angles (tan(a + b) or tan(a - b)) is derived by dividing the sine and cosine formulas for addition or subtraction by cos a * cos b.
Q & A
Why must the angles x, y, and x + y be acute for the geometrical proof to work?
-The geometrical proof for the compound angle formulas requires x, y, and x + y to be acute to ensure that the specific geometric relationships, such as alternate angles and side ratios, hold true. If any of these angles are not acute, the proof may not apply correctly.
What geometric shape is used in the proof and why is it significant?
-The proof uses a rectangle with a right-angled triangle inside it. The geometric shape helps establish the necessary trigonometric relationships by creating right-angled triangles, allowing for the application of sine and cosine rules.
How do the angles in the triangle relate to each other in the proof?
-The angles in the right-angled triangles relate to each other by using complementary angles. For instance, in one triangle, the angle is calculated as 90 - x, and in another, it is 90 - y. These relationships are critical for deducing the compound angle formulas.
How is the sine and cosine of x and y related to the sides of the right-angled triangles?
-In the proof, sine and cosine of x and y are expressed as ratios of the sides of the right-angled triangles. For example, sine x is the opposite side divided by the hypotenuse, and cosine x is the adjacent side divided by the hypotenuse. These relationships are used to express the sides in terms of sine and cosine functions.
What is the significance of using the alternate angle theorem in the proof?
-The alternate angle theorem helps establish relationships between parallel lines and angles. Specifically, it allows for the determination that certain angles, such as x + y, are congruent to alternate angles formed by parallel lines, which is essential for completing the proof.
How is the compound angle formula for sine derived geometrically?
-The compound angle formula for sine is derived by observing the relationship between the sides of the triangles and comparing them. The sum of the sides involving sine x and cosine y, as well as cosine x and sine y, leads to the formula sin(x + y) = sin(x)cos(y) + cos(x)sin(y).
How does the reflection property of sine and cosine help derive the formula for sine of x - y?
-The reflection property states that cos(-y) = cos(y) and sin(-y) = -sin(y). This allows for the derivation of the formula for sin(x - y) by substituting -y into the formula for sin(x + y), which results in sin(x - y) = sin(x)cos(y) - cos(x)sin(y).
Why does the proof maintain the positive signs when dividing by cos(x)cos(y)?
-The positive signs are maintained when dividing by cos(x)cos(y) because x and y are acute angles. In the first quadrant, cosine is positive, meaning the signs will not change during the division, preserving the integrity of the formula.
How does the compound angle formula for tangent relate to the sine and cosine formulas?
-The compound angle formula for tangent is derived by dividing the sine formula by the cosine formula. This results in the formula tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b)), by simplifying the expression using the sine and cosine identities.
What happens to the formula for tan(a + b) when a and b are acute?
-When a and b are acute, both tan(a) and tan(b) are positive. This ensures that the compound angle formula for tangent holds true without requiring any adjustments for negative values, as both sine and cosine remain positive in the first quadrant.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Cara menentukan besar sudut pada sudut berpenyiku berpelurus dan bertolak belakang

Fungsi Eksponen Pertumbuhan dan Peluruhan
2 Missing Angles in a Polygon
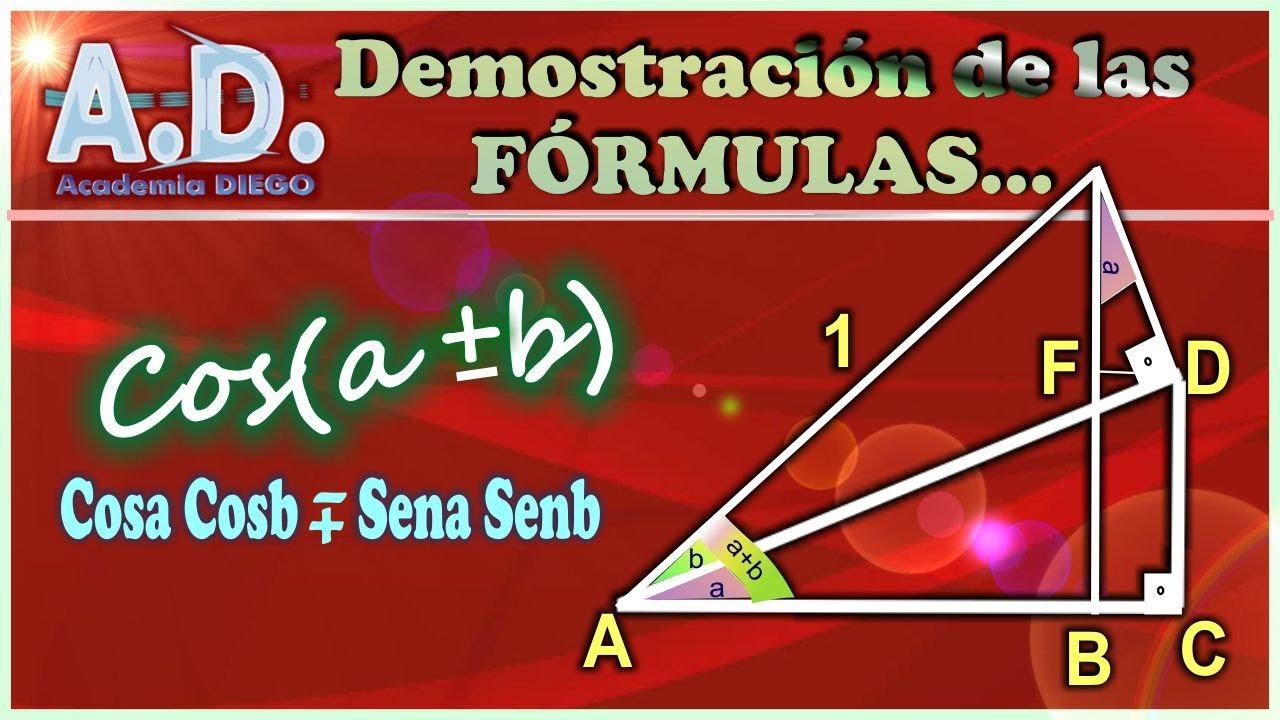
TRIGONOMETRÍA: Cos (a+b) Demostración de la fórmula Academia DIEGO

LATIHAN 2.1 NO 1 SUDUT PUSAT SUDUT KELILING MATEMATIKA SMA KELAS 11 #kurikulummerdeka #matematikasma

Pada gambar di samping, sudut CAB=sudut ZBA=90, X=titik tengah AB, AB=2 AC, dan AB=BZ.Buktikan b...
5.0 / 5 (0 votes)