INV617-W9-BIRT(3)
Summary
TLDRThis video explains the process of valuing bonds with embedded options (callable and putable bonds) using a binomial interest rate tree. The method involves adjusting bond values at each node based on the possibility of the options being exercised. For callable bonds, the value is adjusted to the minimum of the bond value or the call price, while for putable bonds, it’s adjusted to the minimum of the bond value or the put price. The video also covers how to calculate the value of embedded call and put options by comparing the values of option-free and option-adjusted bonds.
Takeaways
- 😀 The process of valuing callable and putable bonds using a binomial interest rate tree is similar to valuing option-free bonds, with adjustments for the embedded options.
- 😀 For callable bonds, the bond value at each node is adjusted to reflect the minimum of its calculated value and the call price if the calculated value exceeds the call price.
- 😀 The call price is the maximum price the issuer will pay to call the bond, and if the calculated value exceeds this, the bond value is adjusted to the call price.
- 😀 In the case of a callable bond, the binomial tree is constructed in four periods: period 0 (initial), period 1, period 2, and period 3 (maturity).
- 😀 For period 3 (maturity), the bond value is simply the par value plus the coupon, as no options are exercised at this stage.
- 😀 When calculating the value at nodes in the binomial tree, use the cash flow from the adjacent nodes and discount it by the appropriate interest rate.
- 😀 If the callable bond's value exceeds the call price at any node, substitute the bond's value with the call price to reflect the issuer's right to call the bond.
- 😀 The value of the call option is calculated as the difference between the value of the non-callable bond and the callable bond.
- 😀 For putable bonds, the valuation process is similar to callable bonds, except the bondholder can put the bond back to the issuer if the value is lower than the put price.
- 😀 The value of the put option is the difference between the value of the non-puttable bond and the putable bond, and the put price serves as the minimum value for putable bonds.
Q & A
What is the primary purpose of using a binomial interest rate tree in bond valuation?
-The binomial interest rate tree is used to model the different possible paths an interest rate might take over time, allowing for the valuation of bonds, including those with embedded options like callable or putable bonds.
How is the process of valuing a callable bond different from valuing an option-free bond?
-The process is similar, but in the case of a callable bond, if the bond's value at any node exceeds the call price, the value is adjusted to the call price. This reflects the issuer's option to call the bond early.
What happens when the value of a callable bond at a node exceeds the call price?
-When the value at a node exceeds the call price, it is adjusted to the call price. This ensures that the callable bond's value reflects the issuer's ability to call the bond back at a set price.
How do you calculate the value of a call option embedded in a callable bond?
-The value of the call option is determined by subtracting the value of the callable bond from the value of the option-free bond. This difference represents the value of the embedded call option.
In the context of putable bonds, what happens when the bond value at a node falls below the put price?
-When the bond value at a node falls below the put price, the value is adjusted to reflect the put price, which ensures that the bondholder can sell the bond back at this minimum value.
How is the process of valuing a putable bond similar to that of valuing a callable bond?
-The process is similar in both cases, but for putable bonds, the minimum value at each node is the put price. If the bond's value is less than the put price, it is adjusted to reflect the put price.
What is the significance of the call price in the valuation of a callable bond?
-The call price acts as a cap on the bond’s value at each node. If the value at a node exceeds the call price, it is replaced with the call price, as this reflects the issuer's ability to redeem the bond early at that price.
Can the put price be higher than the bond's value at any given node during the valuation of a putable bond?
-No, the put price represents the minimum value for the bond. If the bond’s value at a node is higher than the put price, the value remains unchanged; if it is lower, the value is adjusted to the put price.
What are the main differences between a callable bond and a putable bond in terms of valuation?
-The key difference is that in a callable bond, the issuer has the option to call the bond back at a specified price, which caps the bond’s value. In a putable bond, the bondholder has the option to sell the bond back at the put price, which sets a floor on the bond’s value.
Why do you need to adjust bond values at each node when using a binomial interest rate tree for bonds with embedded options?
-Adjustments are necessary to reflect the impact of the embedded options (like call or put options). These adjustments ensure that the bond's value accounts for the possibility of early redemption (in the case of callable bonds) or early sale (in the case of putable bonds).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Floating Rate Bonds (FRB): What are RBI Floating Rate Bonds, Type and How to Invest in FRB

#Part1 Ch 14 Long Term Payable (Bond Payable) - Akuntansi Keuangan Menengah 2
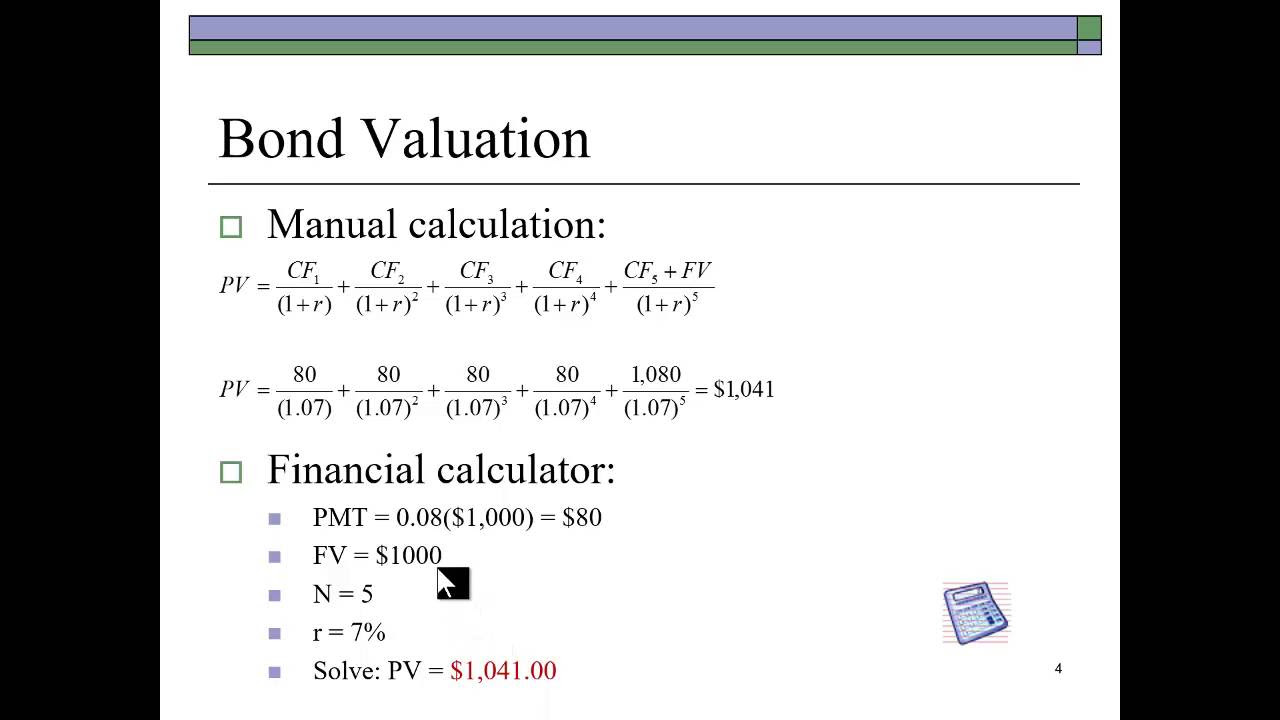
Bond Valuation - A Quick Review

C 1 BOND YTM & YTC

RBI’s Repo Rate Calculations: How Does The RBI Policy Actually Affect You?

Investing Basics: Bonds
5.0 / 5 (0 votes)