Correção exercicio do Barco
Summary
TLDRIn this video script, the speaker explains a projectile motion problem involving a pirate ship and a cannon. The goal is to determine the launch angle and maximum range of a cannonball fired at a pirate ship 560 meters away. Using principles of physics, the speaker demonstrates how to calculate the launch angle using trigonometric equations and how to find the time of flight based on gravitational acceleration. The script also covers the maximum range of the projectile when the angle is adjusted to 45 degrees, providing a detailed, step-by-step breakdown of the solution process.
Takeaways
- 😀 The exercise involves calculating the launch angle and range of a projectile fired from a cannon at a pirate ship located 560 meters away from a fort.
- 😀 The cannonball's initial speed is 82 m/s, and the launch angle is unknown and needs to be calculated.
- 😀 The velocity in the x-direction is constant, given by v0x = 82 * cos(θ), where θ is the unknown launch angle.
- 😀 The velocity in the y-direction is described by v0y = 82 * sin(θ), and this component needs to be used in the calculations.
- 😀 The acceleration due to gravity in the vertical direction is -9.81 m/s², which affects the projectile's motion as it rises and falls.
- 😀 At the peak of the projectile's trajectory, the vertical velocity is zero, as the projectile stops rising before falling back down.
- 😀 The time to reach the highest point is half of the total time, meaning the total time of flight is twice the time to reach the peak.
- 😀 The horizontal motion has no acceleration, so the horizontal distance (range) can be calculated by multiplying the horizontal velocity by the total time of flight.
- 😀 The equation to calculate the total time of flight involves using the vertical motion equation and the gravitational acceleration.
- 😀 The launch angle can be derived using trigonometric identities, resulting in an angle of approximately 27° or its complement 63° to achieve the desired range.
- 😀 When the launch angle is set to 45°, the maximum range is calculated as approximately 685.4 meters, with a total flight time of 11.82 seconds.
Q & A
What is the distance between the pirate ship and the fort?
-The distance between the pirate ship and the fort is 560 meters.
What is the initial velocity of the cannonball?
-The initial velocity of the cannonball is 82.5 meters per second.
What is the gravitational acceleration used in the calculations?
-The gravitational acceleration used in the calculations is -9.81 m/s².
What is the goal of the problem discussed in the transcript?
-The goal is to determine the angle of projection for the cannonball and the maximum range it can achieve.
How is the horizontal distance (range) calculated in the problem?
-The horizontal distance (range) is calculated using the equation x = v₀ cos(θ) * t, where v₀ is the initial velocity, θ is the angle of projection, and t is the time of flight.
Why is the horizontal velocity constant in this problem?
-The horizontal velocity remains constant because there is no acceleration in the horizontal direction, as specified in the problem.
What happens to the vertical velocity at the highest point of the trajectory?
-At the highest point of the trajectory, the vertical velocity becomes zero because the cannonball momentarily stops moving upward before it starts to fall.
How is the total time of flight determined from the vertical motion?
-The total time of flight is twice the time taken to reach the highest point (the time of ascent), which can be calculated using the equation v₀ sin(θ) / g.
How do you solve for the angle of projection, θ, in the problem?
-The angle of projection, θ, is solved by using the equation for horizontal motion and vertical motion, and then applying trigonometric identities. The equation involving sin(2θ) is solved to find the angle.
What is the value of the angle of projection calculated in the solution?
-The angle of projection is calculated to be approximately 27 degrees, with the complementary angle of 63 degrees also being a valid solution.
What is the maximum range of the cannonball when the angle of projection is 45 degrees?
-When the angle of projection is 45 degrees, the maximum range of the cannonball is 685.4 meters.
Why is the time of flight doubled when calculating the total time for the projectile?
-The total time of flight is doubled because the time spent ascending to the highest point is equal to the time spent descending. Therefore, the total flight time is twice the ascent time.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

projectile motion explained
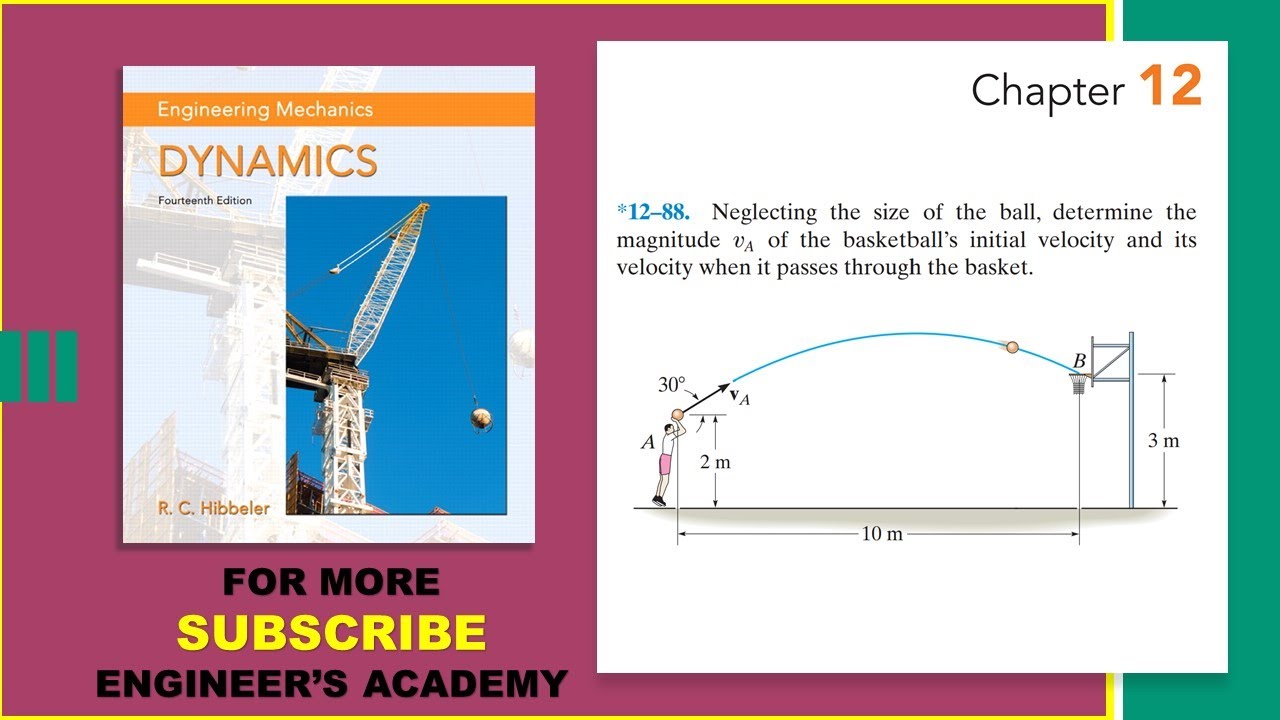
12-88 | Engineering Dynamics Hibbeler 14th Edition | Engineers Academy

Gerak Parabola - Fisika Kelas 10 (Quipper Video)

Física: Movimiento Vertical - Traful Utemvirtual
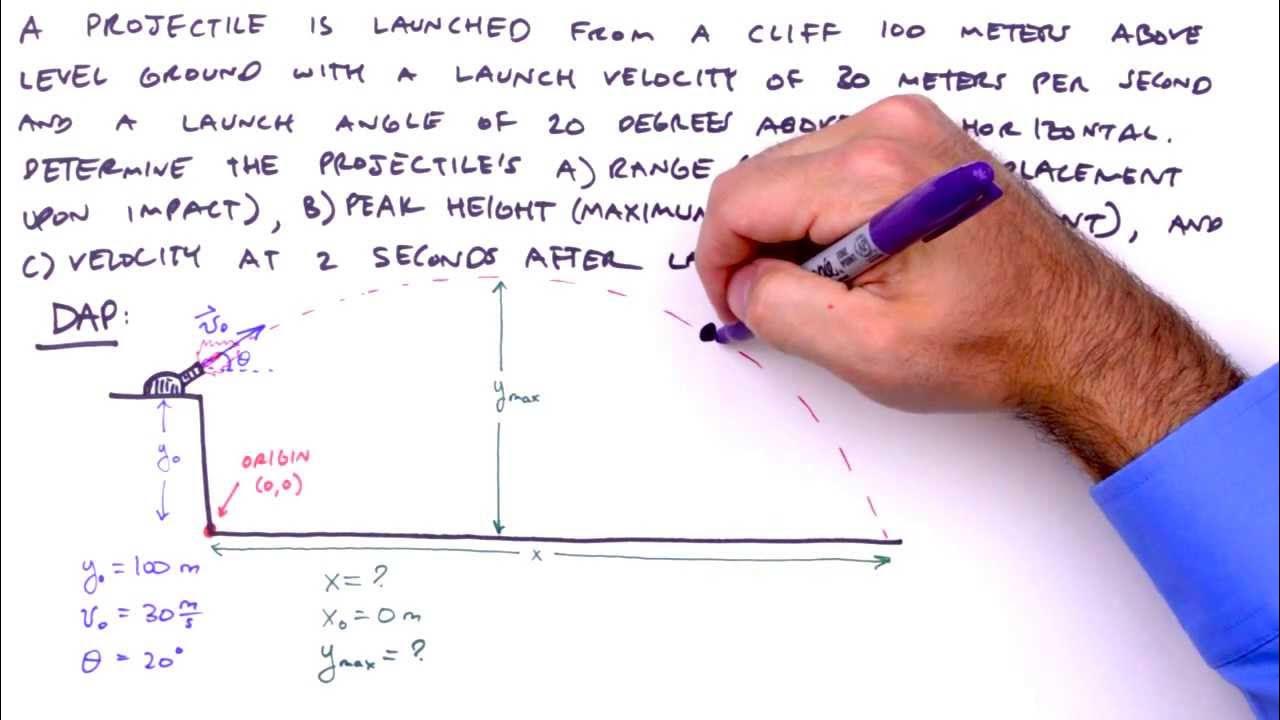
How To Solve Any Projectile Motion Problem (The Toolbox Method)

How Do Horizontally Launched Projectiles Behave? | Physics in Motion
5.0 / 5 (0 votes)