This is the Epsilon Delta Definition of Continuity | Real Analysis
Summary
TLDRThis video provides a thorough explanation of the Epsilon-Delta definition of continuity, a fundamental concept in calculus. It explores how a function is continuous at a point C if the limit of the function as X approaches C equals the function's value at C. The video also introduces equivalent characterizations of continuity and demonstrates how to prove continuity using the Epsilon-Delta definition. Through examples like the identity function, the video shows how this rigorous method can be applied to different functions, explaining important properties and offering an exercise for further practice.
Takeaways
- 😀 The definition of continuity at a point requires the limit of the function as x approaches a point C to equal the function's value at C.
- 😀 The Epsilon-Delta definition of continuity involves finding a Delta for every Epsilon such that if X is within Delta of C, the function value will be within Epsilon of F(C).
- 😀 If C is not a limit point of the domain, a function is trivially continuous at C because the function will always equal F(C) within that region.
- 😀 The main difference between continuity and functional limits is that continuity does not require C to be a limit point of the domain.
- 😀 Continuity can be characterized in multiple ways, including the Epsilon-Delta definition, neighborhood definition, and sequential definition.
- 😀 The sequential definition of continuity states that a function is continuous at C if for all sequences converging to C, the corresponding function values converge to F(C).
- 😀 If C is a limit point, all four definitions of continuity (Epsilon-Delta, neighborhood, limit, and sequential) are equivalent.
- 😀 The identity function f(x) = x is continuous across its entire domain (real numbers) as shown through an Epsilon-Delta proof.
- 😀 To prove continuity using the Epsilon-Delta definition, you pick an arbitrary Epsilon and C, then choose Delta to satisfy the condition that the difference between f(x) and f(C) is less than Epsilon.
- 😀 The continuity of basic functions like f(x) = x leads to the continuity of more complex functions like polynomials and rational functions due to the properties of continuous functions.
- 😀 A practice problem provided encourages proving that the square root function is continuous on its domain (non-negative reals), using a conjugate technique for the proof.
Q & A
What does it mean for a function to be continuous at a point?
-A function is continuous at a point if the limit of the function as x approaches that point equals the function's value at that point.
What is the Epsilon-Delta definition of continuity?
-The Epsilon-Delta definition states that a function f is continuous at a point C if, for every Epsilon greater than zero, there exists a Delta greater than zero such that for all x in the domain, if |x - C| < Delta, then |f(x) - f(C)| < Epsilon.
Why is the definition of continuity related to limits?
-The definition of continuity is closely related to the definition of a limit, as it essentially says that the limit of the function at a point must equal the value of the function at that point for continuity to hold.
What happens when C is not a limit point of the domain in terms of continuity?
-If C is not a limit point of the domain, the function is trivially continuous at C because there will be a small region around C where no other points in the domain exist, forcing f(x) to be equal to f(C).
Why don't we need to specify that |x - C| > 0 in the continuity definition?
-In the definition of continuity, we don't need to specify that |x - C| > 0 because C is part of the domain, so it's fine if x equals C, which contrasts with the definition of a limit where C might not be in the domain.
What are the different characterizations of continuity discussed?
-The four characterizations of continuity discussed are: the Epsilon-Delta definition, the topological definition (using neighborhoods), the limit definition, and the sequential definition (based on sequences converging to C).
How does the sequential definition of continuity differ from the others?
-The sequential definition of continuity states that a function is continuous at C if for every sequence xn converging to C, the sequence of function values f(xn) converges to f(C), which can be used to prove discontinuity without using Epsilons and Deltas.
What is the basic approach to proving a function is continuous using the Epsilon-Delta definition?
-The basic approach is to take an arbitrary Epsilon greater than zero, then find a Delta such that if x is within Delta of C, the distance between f(x) and f(C) is less than Epsilon. For simple functions, you can often choose Delta = Epsilon.
How is the identity function f(x) = x shown to be continuous?
-The identity function f(x) = x is shown to be continuous by taking an arbitrary Epsilon and showing that for any x within Delta of a point C, the distance between f(x) and f(C) is less than Epsilon, with Delta chosen to be equal to Epsilon.
How can the properties of continuity help prove that polynomials are continuous?
-By using the properties of continuity, such as the sum and product of continuous functions being continuous, it follows that polynomials are continuous since they are formed from sums and products of continuous functions like the identity function.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Part 1: Formal Definition of a Limit
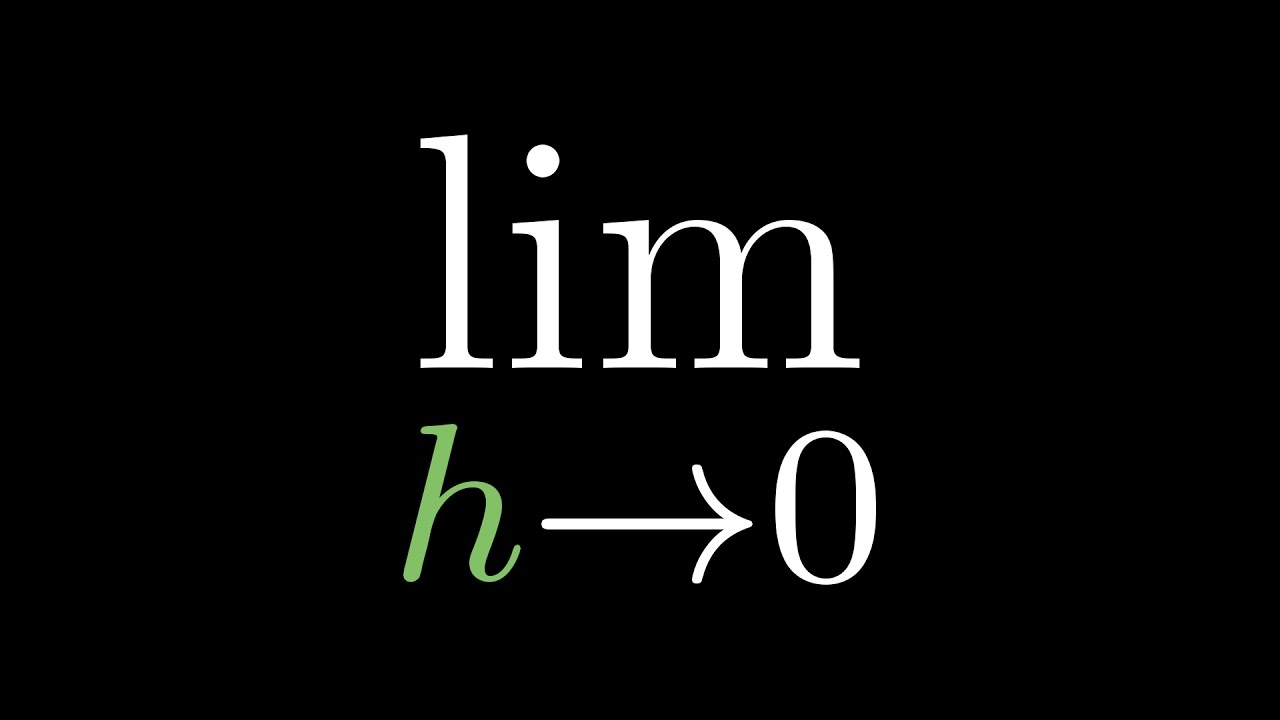
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Limits in Calculus: Definition & Meaning. What is a Limit?

LIMITE: a Ideia Fundamental do Cálculo

Limit of a function | Two Variable Function | Epsilon Delta definition of Limit | Examples

04. Limites e Continuidade. | Cálculo I.
5.0 / 5 (0 votes)