Kalor Jenis Molar Gas | Termodinamika | Part 3 | Fisika Dasar

Summary

This video explores the concept of molar specific heat capacity in gases, detailing the differences between isovolumetric and isobaric processes. It explains the use of formulas to calculate heat and highlights the relationship between the specific heat capacities at constant volume (CV) and pressure (CP). The video emphasizes the importance of understanding these principles when discussing thermodynamic processes, including adiabatic processes and their specific heat ratios. Real-world examples, such as the behavior of monoatomic and diatomic gases, are used to illustrate these concepts, providing viewers with practical knowledge of thermodynamic calculations.

Takeaways

• 😀 The concept of molar specific heat capacity for gases is central to understanding how heat is required to change the temperature of a substance.
• 😀 Molar specific heat (Cm) is commonly used in thermodynamics and depends on the gas type and the process (isovolume or isobaric).
• 😀 Specific heat capacity (C) for different gases may vary and is influenced by their physical properties, especially for non-ideal gases.
• 😀 In isovolume processes, the heat required is calculated using the formula Q = n × Cv × ΔT, where Cv is the specific heat capacity at constant volume.
• 😀 In isobaric processes, the heat required is given by Q = n × Cp × ΔT, where Cp is the specific heat capacity at constant pressure.
• 😀 The relationship between Cp and Cv is important and is described by the equation Cp - Cv = R, where R is the ideal gas constant.
• 😀 The value of Cp is always greater than Cv, as it accounts for the additional work done at constant pressure when the volume can change.
• 😀 For different types of gases, specific heat values are calculated differently. For example, for monoatomic gases, Cv = 3/2 R, and Cp = 5/2 R.
• 😀 The adiabatic index (γ) is the ratio of Cp to Cv and varies for different gases based on their degrees of freedom.
• 😀 To solve practical problems involving heat calculation, formulas for both isovolume and isobaric processes can be used directly, depending on the gas behavior and given conditions.

Q & A

What is molar heat capacity, and how is it different from specific heat capacity?

Molar heat capacity refers to the amount of heat required to change the temperature of one mole of a substance by one degree Celsius. It is different from specific heat capacity, which is the amount of heat needed to raise the temperature of a unit mass of a substance by one degree Celsius.

What is the formula for calculating heat (Q) in terms of molar heat capacity?

The formula for calculating heat (Q) is: Q = n × C_m × ΔT, where n is the number of moles, C_m is the molar heat capacity, and ΔT is the change in temperature.

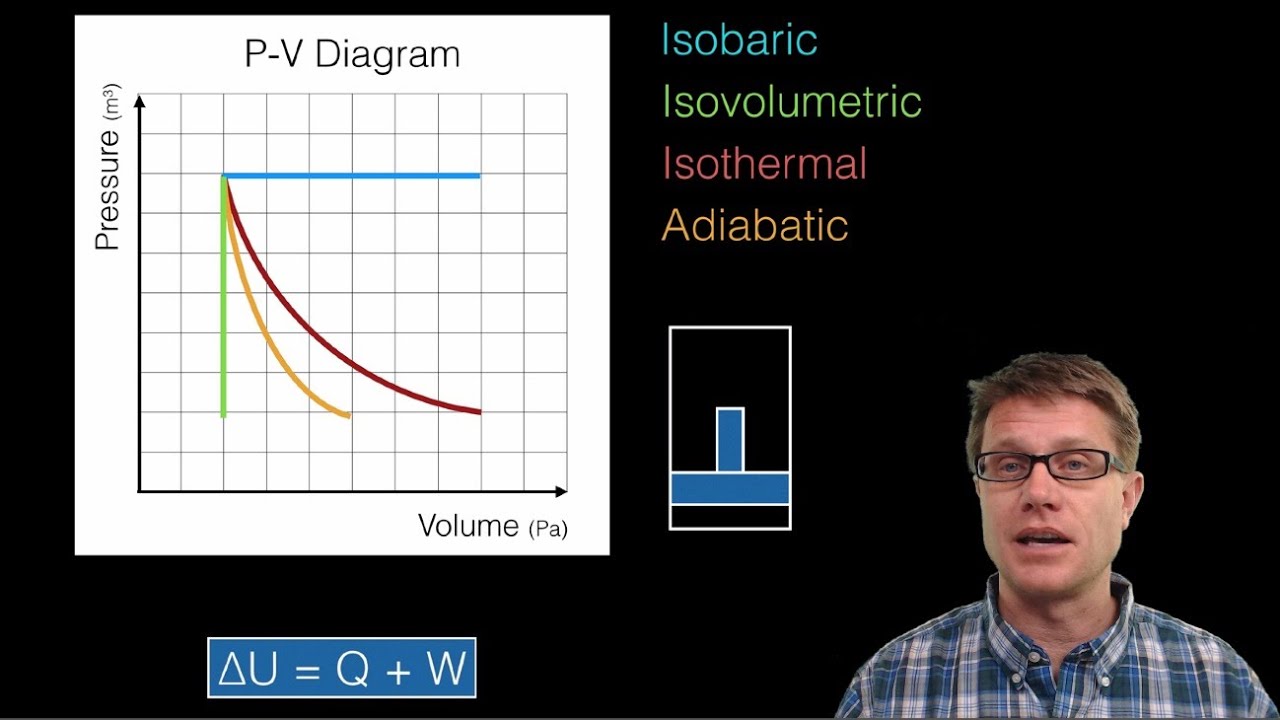
What are isovolumetric and isobaric processes in thermodynamics?

In an isovolumetric (isochoric) process, the volume remains constant, and the heat added results in a change in internal energy. In an isobaric process, the pressure remains constant, and the heat added results in both a change in temperature and work done by the system.

What is the relationship between specific heat capacities at constant pressure (C_P) and constant volume (C_V)?

The relationship between C_P and C_V is given by the equation: C_P - C_V = R, where R is the universal gas constant. This shows that C_P is always greater than C_V.

Why is C_P generally greater than C_V?

C_P is greater than C_V because, during an isobaric process (constant pressure), work is done by the system as it expands, which requires additional heat. In contrast, in an isovolumetric process (constant volume), no work is done, so less heat is required for the same temperature change.

How are the heat capacities for monatomic and diatomic gases different?

For monatomic gases, the molar heat capacity at constant volume (C_V) is 3/2 R, and at constant pressure (C_P) is 5/2 R. For diatomic gases, C_V is 5/2 R, and C_P is 7/2 R, due to the additional degrees of freedom in diatomic molecules.

What is the significance of the heat capacity ratio (γ), and how is it calculated?

The heat capacity ratio (γ) is the ratio of C_P to C_V, and it is an important property of gases, particularly for adiabatic processes. It is calculated as γ = C_P / C_V.

How do the values of C_P and C_V affect the behavior of gases during adiabatic processes?

During an adiabatic process, where no heat is exchanged with the surroundings, the heat capacities C_P and C_V influence the temperature and pressure relationship of the gas. The ratio γ = C_P / C_V affects how the gas's temperature and pressure change when the volume changes adiabatically.

What is the formula for the work done in an isobaric process?

In an isobaric process, the work done by the gas is given by the formula: W = P × ΔV, where P is the constant pressure and ΔV is the change in volume.

How can the first law of thermodynamics be applied to calculate heat in a system?

The first law of thermodynamics states that the change in internal energy (ΔU) is equal to the heat added to the system (Q) minus the work done by the system (W). This can be expressed as ΔU = Q - W, which allows the calculation of heat when internal energy and work are known.