Menghitung Tinggi Menara Dengan Bayangannya
Summary
TLDRIn this educational video, the presenter explains how to calculate the height of a tower using its shadow. By applying the concept of similar triangles, viewers learn to compute the height through basic measurements, such as the distance from the tower and the distance from the observer to the shadow. The video also introduces trigonometry, specifically the tangent function, to solve the same problem. The presenter provides step-by-step instructions and demonstrates how both methods give the same result. This practical lesson can be applied to calculate the heights of flags, trees, buildings, and more, making it valuable for both students and teachers.
Takeaways
- 😀 The video explains how to calculate the height of a tower using its shadow.
- 😀 The method can also be applied to calculate the height of other objects like flags, trees, and buildings.
- 😀 The process involves using the concept of similar triangles, specifically the relationship between the shadow of the tower and the shadow of the person.
- 😀 The distance from the tower to the tip of its shadow is 15 meters, while the distance from the person to the tip of their shadow is 3 meters.
- 😀 The height of the person is 1.6 meters, which is key for applying the concept of similar triangles.
- 😀 The relationship between the heights and distances is derived from the proportion of similar triangles: the person's shadow to the tower's shadow equals the person's height to the tower's height.
- 😀 Using the proportional relationship, the formula is: 3/15 = 1.6/Tower Height.
- 😀 By solving the proportion through cross-multiplication, the height of the tower (TM) is calculated as 8 meters.
- 😀 An alternative method using trigonometry is also explained, where the tangent of the angles formed by the tower and the person are set equal to each other.
- 😀 The tangent formula involves the same proportional relationship and gives the same result of 8 meters for the height of the tower.
- 😀 The video concludes by offering further clarification in the comments section for any additional questions from viewers.
Q & A
What is the primary objective of the script?
-The primary objective is to teach how to calculate the height of a tower using the length of its shadow, a technique that can also be applied to other objects like trees, flags, or buildings.
What information is needed to calculate the height of the tower using its shadow?
-You need the distance from the base of the tower to the tip of the shadow (15 meters), the distance from the observer to the tip of their shadow (3 meters), and the height of the observer (1.6 meters).
How is the similarity of triangles used in this calculation?
-The script uses the principle of similar triangles, where the ratio of corresponding sides of the two triangles (one formed by the tower and its shadow, and the other by the observer and their shadow) are equal. This ratio allows for the calculation of the tower's height.
What is the formula derived from the similarity of triangles?
-The formula is: (distance from observer to shadow / distance from tower to shadow) = (height of observer / height of tower), which can be written as 3/15 = 1.6/TM, where TM represents the height of the tower.
How is the final height of the tower calculated?
-By cross-multiplying, the equation becomes 3 * TM = 15 * 1.6, which simplifies to 3 * TM = 24. Solving for TM gives a result of TM = 24/3 = 8 meters.
What alternative method is mentioned for calculating the tower's height?
-The script also introduces the trigonometric method using the tangent of the angle formed by the top of the tower and its shadow, and the angle formed by the observer and their shadow. The tangent formula for both angles is set equal to each other.
How does the trigonometric method work in this context?
-The tangent of angle BAC (related to the tower) is set equal to the tangent of angle DAE (related to the observer). The equation is TM/15 = 1.6/3, which is then solved by cross-multiplying to find TM = 8 meters, just as in the first method.
What are the advantages of using the similarity of triangles method?
-The similarity of triangles method is straightforward and relies on basic geometric principles, making it easier to understand and apply for most students without requiring advanced knowledge of trigonometry.
Why does the script mention using both methods for calculating the tower's height?
-By presenting both the similarity of triangles method and the trigonometric method, the script caters to students with different levels of understanding, allowing them to choose the method they are most comfortable with or best suited for the situation.
What does the script recommend for teachers or students after learning the method?
-The script encourages teachers to use this technique as a practical exercise in mathematics to help students develop logical and systematic thinking skills. It also invites students to ask questions in the comments if they need further clarification.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
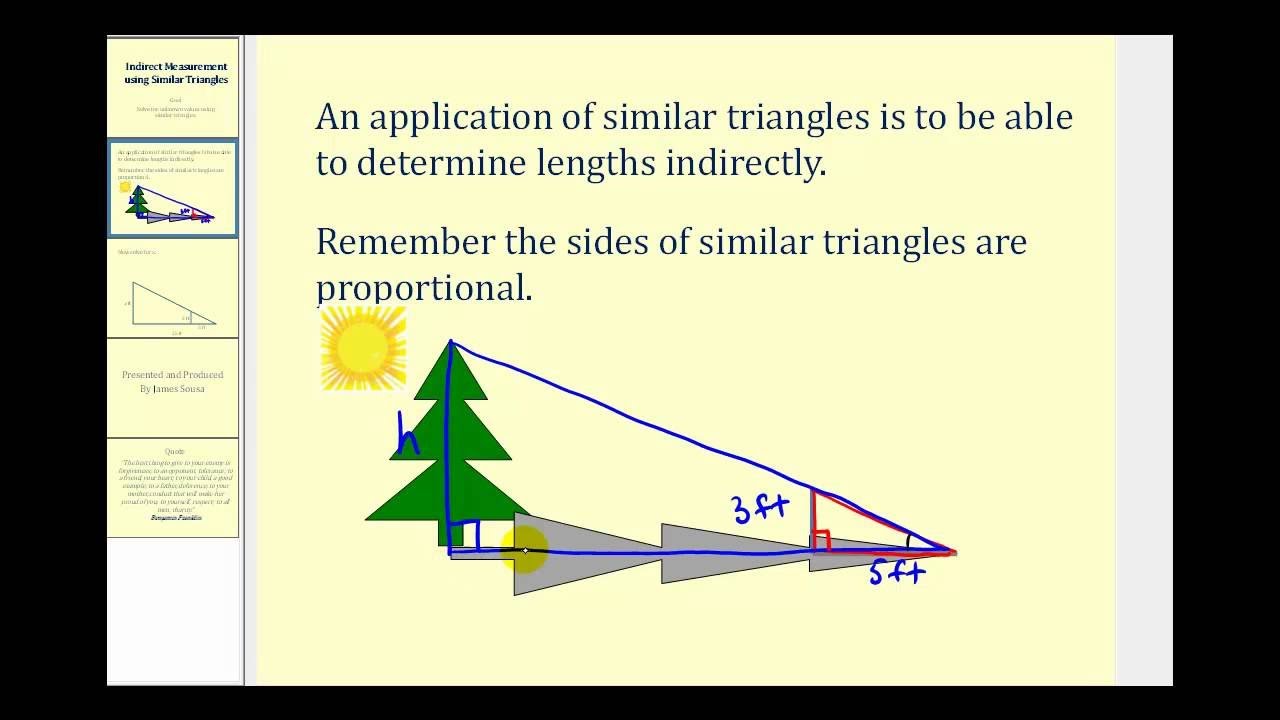
Medición indirecta utilizando triángulos similares

FREE FALL PHYSICS PERFORMANCE TASK

IGCSE Physics [Syllabus 1.8] Pressure
FÁCIL E RÁPIDO | ÁREA DO TRIÂNGULO - GEOMETRIA

CARA MENGHITUNG TINGGI TIANG BENDERA DENGAN MENGGUNAKAN RUMUS TRIGONOMETRI #trigonometry #matematika

Sides Ratio of a Special Angled Triangle - Part 5 Pythagoras Series - Grade 8th
5.0 / 5 (0 votes)