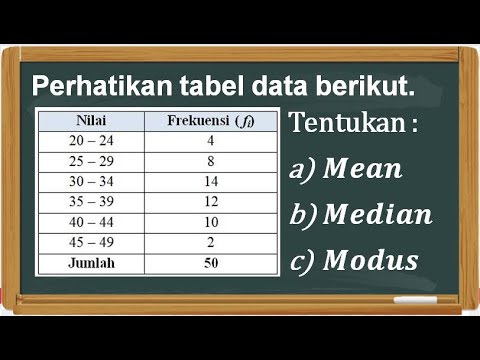
mean median modus data tunggal dalam bentuk tabel

Summary

This educational video explains how to calculate the mean, median, and mode of a dataset presented in a table format. The tutorial demonstrates the process for calculating the mean by multiplying each data value by its frequency, followed by summing and dividing by the total frequency. For the median, the script explains how to handle even-numbered datasets by averaging the 10th and 11th data points. Lastly, the mode is determined by identifying the value with the highest frequency. The lesson provides clear examples to help viewers understand these statistical concepts effectively.

Takeaways

• 😀 The script explains how to calculate the mean, median, and mode for data presented in a frequency table.
• 😀 The mean (average) is calculated by multiplying each data value by its frequency, summing these products, and dividing by the total number of data points.
• 😀 To find the median for an even number of data points, use the formula: Median = (X₁₀ + X₁₁) / 2.
• 😀 The mode is the data value that appears most frequently in the dataset. If there are multiple values with the same highest frequency, the dataset is bimodal or multimodal.
• 😀 For the example provided, the mean is calculated as 12.
• 😀 The median is found by identifying the 10th and 11th data points and averaging them, resulting in a median of 12.5.
• 😀 The mode is the value with the highest frequency in the dataset, which is 15 in this case.
• 😀 The script stresses the importance of correctly handling both odd and even numbers of data points when calculating the median.
• 😀 The calculation of the mean involves adding the products of data values and their frequencies, then dividing by the total frequency.
• 😀 The script uses a clear step-by-step approach to guide through calculating mean, median, and mode from a frequency table for beginners.

Q & A

What is the formula to calculate the mean of a dataset in this script?

The formula to calculate the mean is the sum of all (data values multiplied by their frequencies) divided by the total frequency: Mean = (Sum of Data × Frequency) / Total Frequency.

How did the speaker calculate the total sum of data in the script?

The speaker calculated the total sum by multiplying each data value by its frequency, then summing up the results: 5×4 = 20, 10×6 = 60, 15×8 = 120, 20×2 = 40, and adding these: 20 + 60 + 120 + 40 = 240.

What is the total frequency (number of data points) in the script?

The total frequency is calculated by summing the individual frequencies: 4 + 6 + 8 + 2 = 20.

What is the mean of the dataset based on the calculations provided in the script?

The mean is 12, calculated by dividing the total sum of data (240) by the total frequency (20), resulting in 240 / 20 = 12.

What is the formula for calculating the median for an even number of data points?

The formula for the median when the number of data points (n) is even is: Median = (X(n/2) + X((n/2)+1)) / 2.

How did the speaker determine which data points corresponded to the 10th and 11th positions in the dataset?

The speaker examined the cumulative frequency distribution to find that the 10th data point is the value 10, and the 11th data point is the value 15.

What was the final median value calculated in the script?

The final median value was 12.5, calculated by averaging the 10th and 11th data points: (10 + 15) / 2 = 12.5.

What is the mode of the dataset in the script?

The mode is the value that appears most frequently in the dataset. In this case, the value 15 appears 8 times, making it the mode.

What happens if there are two values with the same highest frequency in a dataset?

If there are two values with the same highest frequency, the dataset has two modes, which is known as bimodal.

Why is it important to understand the difference between odd and even numbers of data points when calculating the median?

Understanding the difference is important because the formula for calculating the median differs depending on whether the number of data points is odd or even. For even datasets, the median is the average of the two middle values, while for odd datasets, it is simply the middle value.