Pares ordenados y producto cartesiano

Summary

En este video se abordan los conceptos de pares ordenados y producto cartesiano. Se explica cómo situar un par ordenado en el plano cartesiano, destacando que la abscisa y la ordenada son componentes clave. Se desarrolla un ejemplo práctico para ilustrar cómo trabajar con ecuaciones involucradas en pares ordenados. Además, se profundiza en el producto cartesiano de dos conjuntos, mostrando cómo formar pares ordenados a partir de los elementos de los conjuntos, y cómo graficar estos productos cuando los conjuntos tienen elementos finitos o infinitos. El video concluye con una visualización gráfica y explicación de las fronteras en productos cartesianos infinitos.

Takeaways

• 😀 Un par ordenado es una pareja de números representados por (x, y), donde x es la abscisa y y es la ordenada.
• 😀 Para ubicar un par ordenado en el plano cartesiano, se deben mover x unidades en el eje horizontal y y unidades en el eje vertical.
• 😀 Si dos pares ordenados son iguales, sus abscisas y ordenadas son iguales.
• 😀 Al resolver ecuaciones que involucran pares ordenados, se pueden despejar las variables para encontrar sus valores.
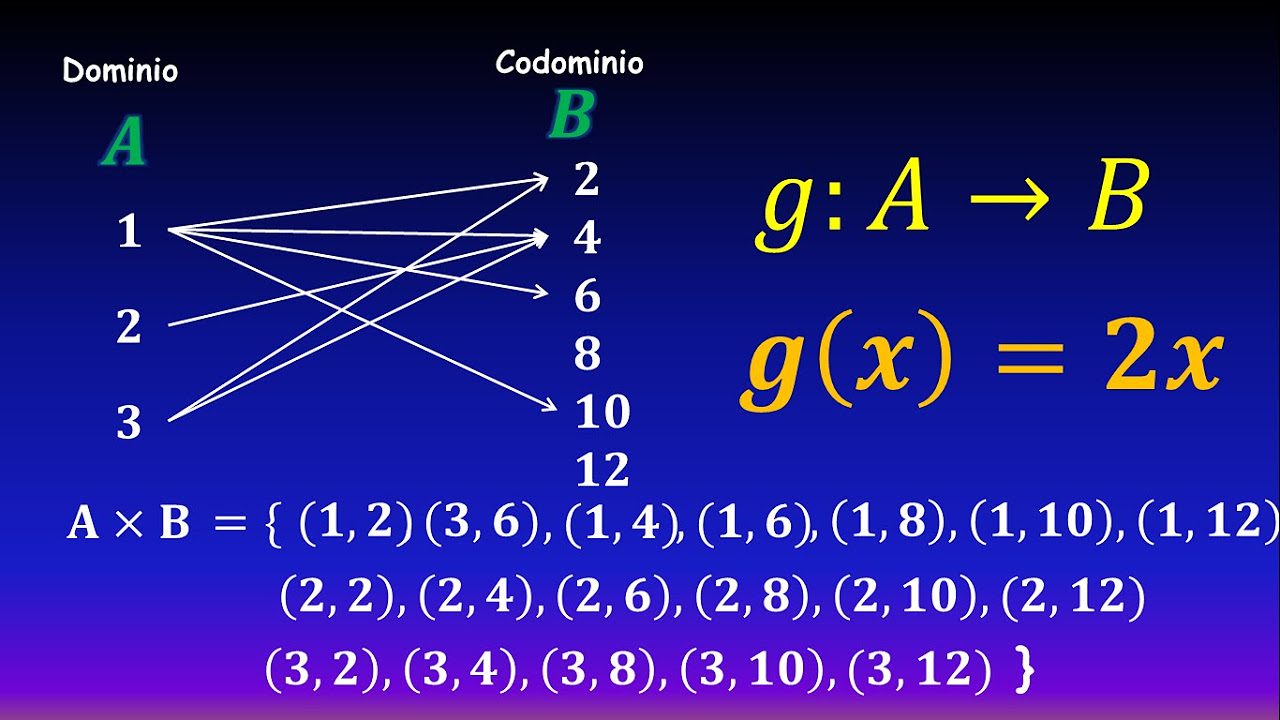
• 😀 El producto cartesiano de dos conjuntos A y B genera un nuevo conjunto de pares ordenados (a, b), donde a pertenece al conjunto A y b pertenece al conjunto B.
• 😀 El número de elementos en el producto cartesiano de dos conjuntos es el producto de la cantidad de elementos en cada conjunto.
• 😀 El producto cartesiano de A x B no es igual a B x A, ya que el orden de las componentes en los pares ordenados cambia.
• 😀 Cuando los conjuntos son finitos, el producto cartesiano tiene un número limitado de pares ordenados, y se puede visualizar gráficamente.
• 😀 Si los conjuntos son infinitos, el producto cartesiano genera una región en el plano cartesiano, que se puede representar gráficamente mediante intervalos.
• 😀 Cuando graficamos el producto cartesiano de intervalos, las fronteras del gráfico se incluyen o excluyen dependiendo de si los extremos del intervalo están incluidos o no.
• 😀 Es importante tener en cuenta que un punto en la frontera de la región del producto cartesiano puede pertenecer o no, dependiendo de si está dentro de los intervalos definidos por los conjuntos.

Q & A

¿Qué es un par ordenado?

Un par ordenado es una pareja de números en la que la primera componente se llama abscisa y la segunda se llama ordenada. Estos pares se usan para representar puntos en el plano cartesiano.

¿Cómo se ubica un par ordenado en el plano cartesiano?

Para ubicar un par ordenado en el plano cartesiano, primero nos movemos 'x' unidades en el eje horizontal (eje X) y luego 'y' unidades en el eje vertical (eje Y), para situar el punto correspondiente.

¿Qué significa que dos pares ordenados sean iguales?

Si dos pares ordenados son iguales, significa que tanto las abscisas como las ordenadas de ambos pares son iguales, es decir, el valor 'x' de ambos pares es el mismo y el valor 'y' también es el mismo.

En el ejemplo de la ecuación 'x = 5/3 y = 2', ¿cómo se obtuvo el valor de 's'?

El valor de 's' se obtuvo sustituyendo los valores de 'x' y 'y' en la fórmula de 's = 2x + 3'. Al hacerlo, se obtiene 's = 20'.

¿Qué es el producto cartesiano de dos conjuntos?

El producto cartesiano de dos conjuntos A y B es el conjunto de todos los pares ordenados (a, b), donde 'a' pertenece al conjunto A y 'b' pertenece al conjunto B.

¿Cómo se determina el número de elementos en el producto cartesiano de dos conjuntos finitos?

El número de elementos en el producto cartesiano de dos conjuntos finitos se determina multiplicando el número de elementos de cada conjunto. Por ejemplo, si A tiene 3 elementos y B tiene 2 elementos, el producto cartesiano tendrá 6 elementos.

¿Cuál es la diferencia entre el producto cartesiano A × B y B × A?

La diferencia radica en que en A × B, la primera componente de cada par ordenado pertenece a A y la segunda a B. En B × A, la primera componente pertenece a B y la segunda a A. Estos productos no son iguales, salvo que A y B tengan los mismos elementos.

¿Qué sucede cuando los conjuntos involucrados en el producto cartesiano tienen elementos infinitos?

Cuando los conjuntos tienen elementos infinitos, no se puede representar el producto cartesiano con una lista de pares ordenados. En su lugar, se representa gráficamente, creando una región en el plano cartesiano, en lugar de puntos aislados.

¿Cómo se grafica el producto cartesiano cuando los conjuntos son intervalos con elementos infinitos?

Se grafica situando los intervalos de los conjuntos A y B en los ejes X y Y, respectivamente, y luego trazando líneas perpendiculares a estos ejes para formar un rectángulo. Si los extremos de los intervalos están incluidos, se marcan los bordes del rectángulo, de lo contrario, se dejan abiertos.

¿Qué significa que un punto esté dentro del producto cartesiano en una representación gráfica?

Un punto está dentro del producto cartesiano si sus coordenadas cumplen con las condiciones de pertenecer a los intervalos de los conjuntos A y B. Esto significa que tanto su valor en el eje X como en el eje Y deben estar dentro de los intervalos respectivos.