#AYOBELAJAR MATEMATIKA | JUMLAH DAN HASIL KALI AKAR-AKAR PERSAMAAN KUADRAT
Summary
TLDRIn this educational video, the presenter explains how to calculate the sum and product of the roots of a quadratic equation. Through detailed examples, viewers learn to use formulas such as -b/a for the sum and c/a for the product of the roots, without needing to find the roots themselves. The video also covers additional formulas related to quadratic equations, including sums of squared roots and reciprocal sums. Several practice problems help clarify the concepts, demonstrating the practical application of these formulas in solving quadratic equations.
Takeaways
- 😀 To calculate the sum and product of the roots of a quadratic equation, you can use formulas without explicitly finding the roots.
- 😀 The sum of the roots (x1 + x2) can be determined using the formula -b/a, where 'b' is the coefficient of x and 'a' is the coefficient of x^2 in the quadratic equation.
- 😀 The product of the roots (x1 * x2) can be determined using the formula c/a, where 'c' is the constant term in the quadratic equation.
- 😀 For a quadratic equation of the form ax^2 + bx + c = 0, you can find the sum of the roots by calculating -b/a and the product of the roots by calculating c/a.
- 😀 If the quadratic equation is in factored form, such as (x - 3)(x + 1) = 0, the roots can be directly found as x = 3 and x = -1.
- 😀 The sum and product of the roots can be verified by factoring the quadratic equation and checking if the calculated sum and product match the roots.
- 😀 There are additional formulas involving the squares and cubes of the roots, such as x1^2 + x2^2, which can be derived and used in various problems.
- 😀 When dealing with reciprocal sums (1/x1 + 1/x2), you can use the formula (x1 + x2) / (x1 * x2) to simplify the calculation.
- 😀 The script explains several example problems, demonstrating how to use the sum and product of the roots formulas for different quadratic equations.
- 😀 For quadratic equations with more complex structures or given roots as variables (like Alfa and Beta), the formulas can be adapted to solve for unknown values.
Q & A
What is the main focus of the video script?
-The main focus of the video is teaching how to calculate the sum and product of the roots of a quadratic equation without directly solving for the roots using the quadratic formula.
How can the sum and product of the roots of a quadratic equation be calculated without solving for the roots?
-The sum of the roots can be calculated using the formula -b/a, and the product of the roots can be calculated using the formula c/a, where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c = 0.
What is the significance of using the quadratic formula in the script?
-The quadratic formula is used to find the roots of a quadratic equation, but in the script, it is shown that the sum and product of the roots can be derived directly from the coefficients, making it a simpler approach in some cases.
Can you explain the relationship between the roots and the coefficients of a quadratic equation?
-Yes, in a quadratic equation ax^2 + bx + c = 0, the sum of the roots (x1 + x2) is -b/a, and the product of the roots (x1 * x2) is c/a. These relationships allow for the calculation of the roots' sum and product without solving for the individual roots.
How do you find the sum of the roots for the equation x^2 - 2x - 3 = 0?
-For the equation x^2 - 2x - 3 = 0, the sum of the roots can be calculated as -(-2)/1, which equals 2.
What formula is used to calculate the sum of the reciprocals of the roots?
-The formula for the sum of the reciprocals of the roots is (x1 + x2) / (x1 * x2). This formula combines the sum and product of the roots to calculate the sum of their reciprocals.
What is the sum of the reciprocals of the roots for the equation 3x^2 - 9x + 4 = 0?
-The sum of the reciprocals of the roots is calculated as (x1 + x2) / (x1 * x2). From the equation 3x^2 - 9x + 4 = 0, the sum of the roots is -(-9)/3 = 3, and the product is 4/3. Therefore, the sum of the reciprocals is 3 / (4/3), which equals 9/4.
What steps should be followed when solving for the product of the roots in a quadratic equation?
-To find the product of the roots, use the formula c/a, where c is the constant term and a is the coefficient of x^2. For example, in the equation 2x^2 - 6x - p = 0, the product of the roots is -p/2.
How can we calculate the value of 'p' in the equation 2x^2 - 6x - p = 0, given that the difference between the roots is 5?
-First, calculate the sum of the roots using -(-6)/2 = 3. Then, use the given difference between the roots, x1 - x2 = 5, to find the value of the roots. Finally, use the formula for the product of the roots to solve for p, yielding p = 8.
What is the value of 'p' when solving for the quadratic equation 2x^2 - 6x - p = 0, where the difference of the roots is 5?
-In the given equation, after calculating the sum of the roots and using the difference, the value of 'p' is found to be 8.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Akar-akar persamaan kuadrat : Rumus jumlah dan hasil kali akar persamaan kuadrat

Persamaan Kuadrat [Part 5] - Menyusun Persamaan Kuadrat Baru
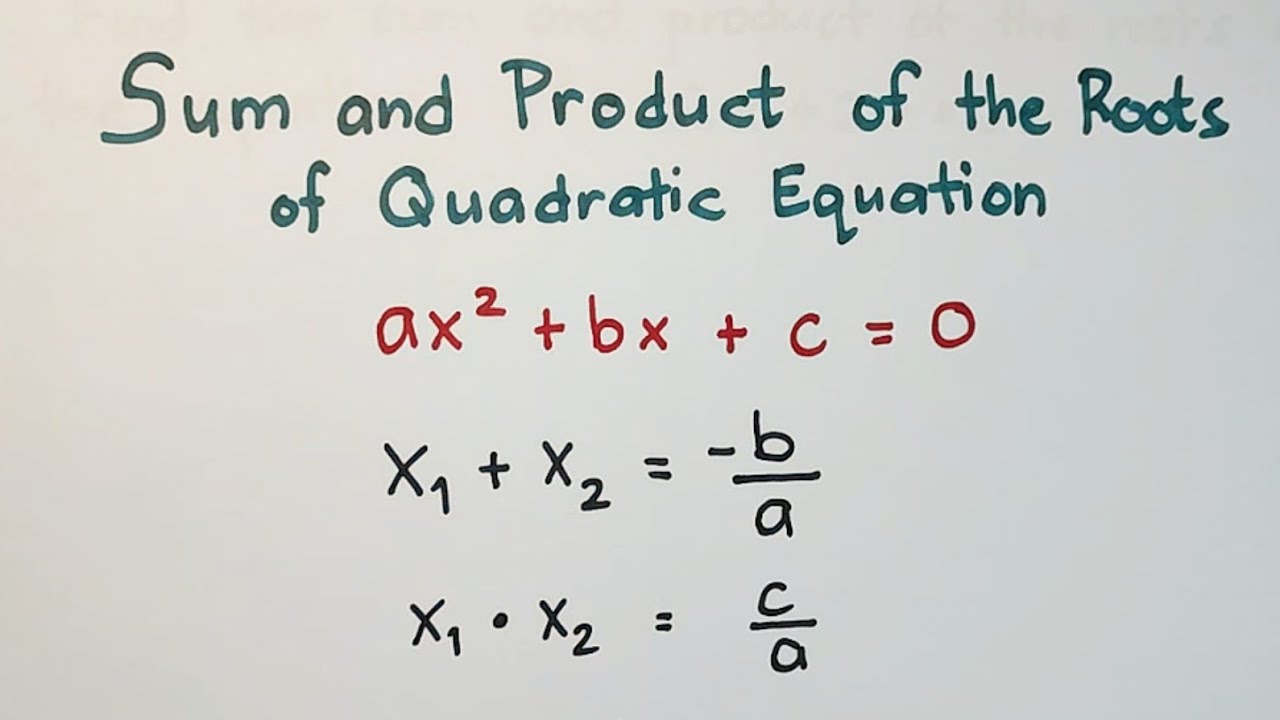
Sum and Product of the Roots of Quadratic Equation - Finding the Quadratic Equation

Matematika SMA - Persamaan Kuadrat (2) - Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

TRIK MENGUASAI SOAL PERSAMAAN KUADRAT BARU‼️

MATH9 DISCRIMINANT and NATURE OF ROOTS of quadratic equation #math9 #discriminant #natureofroots
5.0 / 5 (0 votes)