Properties of Relations in Discrete Math (Reflexive, Symmetric, Transitive, and Equivalence)

Summary

This video explains key properties of relations on sets, focusing on reflexivity, symmetry, transitivity, and equivalence relations. The concept of a relation is explored through examples involving directed graphs and matrices. Reflexivity means every element is related to itself, symmetry requires reciprocal relations, and transitivity ensures that relationships between elements extend through connections. The video concludes with the definition of an equivalence relation, which must satisfy all three properties. Visual representations and matrix analysis help simplify the understanding of these abstract concepts, making them more accessible for learners.

Takeaways

• 😀 Reflexive Property: A relation is reflexive if every element of a set is related to itself. This can be represented visually with loops in a directed graph or by checking the diagonal of a matrix.
• 😀 Symmetric Property: A relation is symmetric if, for every pair (a, b), the reverse pair (b, a) is also in the relation. In a directed graph, this means every arrow has a counterpart in the opposite direction.
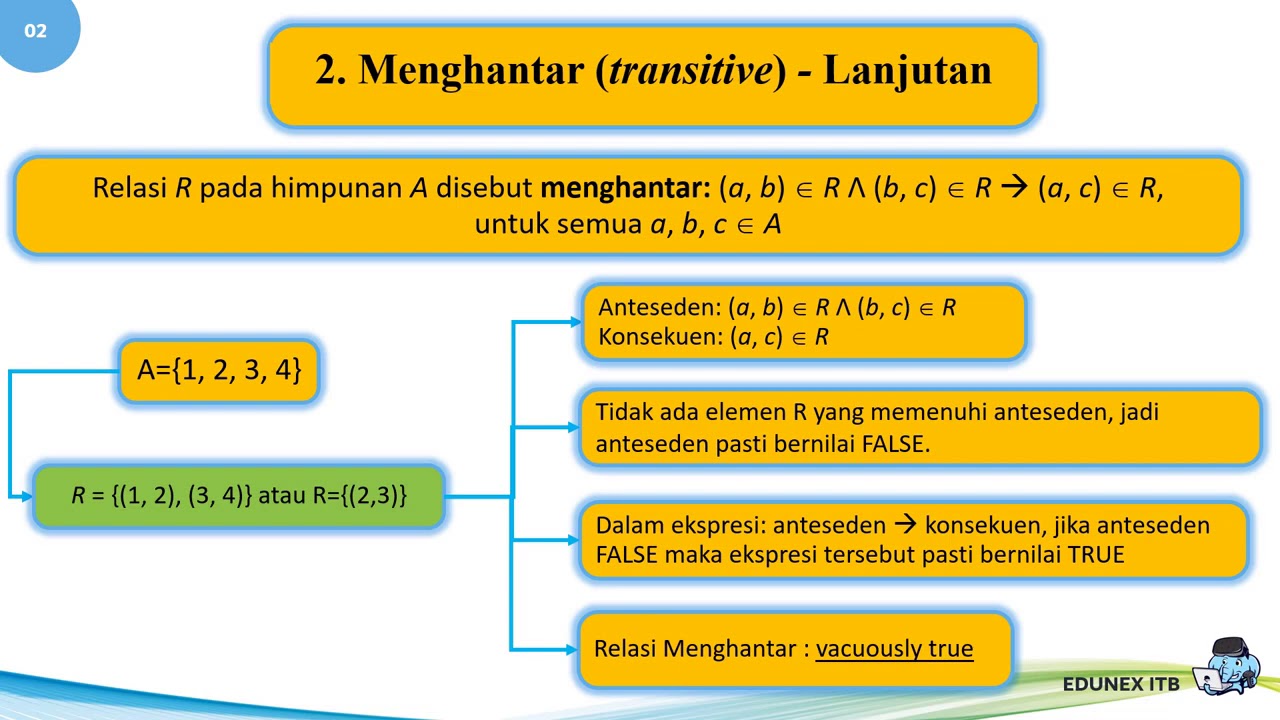
• 😀 Transitive Property: A relation is transitive if, whenever (a, b) and (b, c) are in the relation, (a, c) must also be in the relation. This property can be checked by examining paths in a directed graph or by squaring the matrix.
• 😀 Reflexivity Check with Matrices: A matrix representation of a relation can help check reflexivity by ensuring all diagonal elements are 1. If any diagonal element is 0, the relation is not reflexive.
• 😀 Symmetry Check with Matrices: A relation is symmetric if its matrix is equal to its transpose. If flipping the matrix over its diagonal results in the same matrix, the relation is symmetric.
• 😀 Matrix Squaring for Transitivity: To check transitivity, square the matrix. If there is a non-zero value in the squared matrix at position (a, c), there must also be a non-zero value in the original matrix at (a, c) for the relation to be transitive.
• 😀 Equivalence Relation: A relation that is reflexive, symmetric, and transitive is called an equivalence relation. Equivalence relations partition a set into equivalence classes.
• 😀 Directed Graphs for Visualizing Relations: Directed graphs are useful for visualizing the properties of relations. Vertices represent elements, and edges (arrows) represent the relationships between them.
• 😀 Complex Relations: Some relations may not immediately be recognizable as reflexive, symmetric, or transitive without using representations like directed graphs or matrices to help identify the properties.
• 😀 Matrix Representation of Relations: The matrix representation is a powerful tool for understanding relations. It can be used to check reflexivity, symmetry, and transitivity in an easy-to-read format.

Q & A

What does it mean for a relation to be reflexive?

A relation is reflexive if for every element 'a' in the set 'A', the pair (a, a) is included in the relation. This means each element is related to itself.

How can a reflexive relation be represented graphically?

In a directed graph, a reflexive relation is represented by a loop at each vertex, indicating that every element is related to itself.

What role does a matrix play in identifying reflexivity?

In a matrix, a relation is reflexive if the diagonal contains only ones, meaning every element is related to itself. If there is any zero on the diagonal, the relation is not reflexive.

What defines a symmetric relation?

A relation is symmetric if, for every pair (a, b) in the relation, the pair (b, a) must also be in the relation. This means that if one element is related to another, the second element is related back to the first.

How can a symmetric relation be identified in a directed graph?

In a directed graph, a symmetric relation is characterized by bidirectional arrows between vertices. If there's an arrow from 'a' to 'b', there must also be an arrow from 'b' to 'a'.

How can we tell if a relation is symmetric using a matrix?

A relation is symmetric if its matrix is equal to its transpose. This means that the matrix's values on the opposite sides of the diagonal must be identical.

What is the transitive property in a relation?

A relation is transitive if whenever (a, b) and (b, c) are in the relation, the pair (a, c) must also be in the relation. In other words, if 'a' is related to 'b' and 'b' is related to 'c', then 'a' should be related to 'c'.

How does a matrix help in checking the transitive property?

To check transitivity using a matrix, you square the matrix. If there's a path of length 2 (represented by a 1 in the squared matrix), there must also be a direct path of length 1 (a 1 in the original matrix) connecting the same elements.

What is an equivalence relation?

An equivalence relation is a relation that is reflexive, symmetric, and transitive. These three properties must hold for a relation to be considered an equivalence relation.

Why are digraphs and matrices useful for analyzing relations?

Digraphs and matrices help visualize and represent relations more clearly. They make it easier to check for properties like reflexivity, symmetry, and transitivity, which may be difficult to identify directly from the set itself.