CONJUNTOS DOS NÚMEROS REAIS | APRENDA RÁPIDO!

Summary

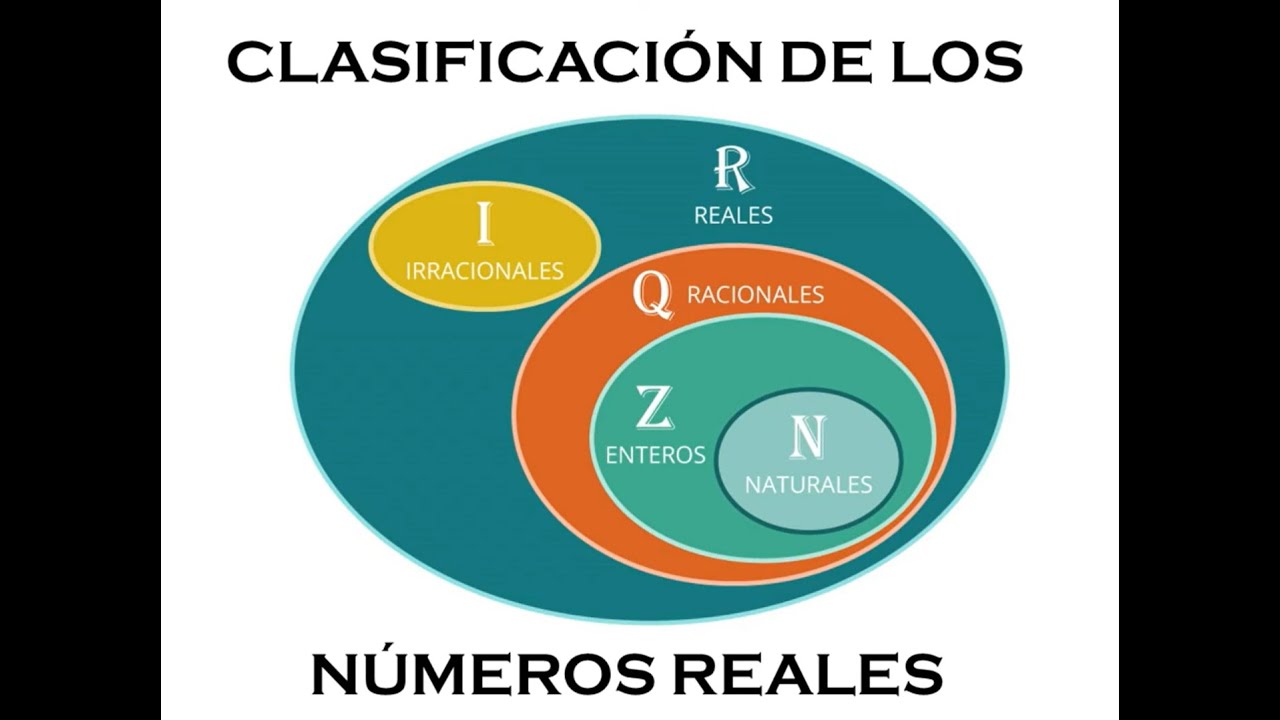
This video explains the concept of real numbers and their subsets, including natural numbers, integers, rational numbers, and irrational numbers. The speaker uses visual aids, such as a Venn diagram, to show the relationships between these sets. Rational numbers are defined as fractions, while irrational numbers, like √2 and π, cannot be expressed as fractions. The video concludes with a quiz on the properties of real numbers, inviting viewers to engage by answering the questions and subscribing to the channel for further learning.

Takeaways

• 😀 Real numbers (R) include both rational and irrational numbers.
• 😀 Rational numbers (Q) can be expressed as fractions, including both positive and negative integers.
• 😀 Irrational numbers cannot be written as fractions and have non-repeating, infinite decimal expansions.
• 😀 Natural numbers (N) are the set of positive counting numbers (1, 2, 3, ...).
• 😀 Integers (Z) include all natural numbers as well as their negatives (e.g., -1, -2, 0, 1, 2, ...).
• 😀 Rational numbers include integers, fractions, and repeating or terminating decimals.
• 😀 Irrational numbers include values like √2 and π, which cannot be written as fractions or repeating decimals.
• 😀 A Venn diagram is used to visualize the relationships between sets of numbers like natural numbers, integers, rational numbers, and irrational numbers.
• 😀 The set of real numbers encompasses all rational and irrational numbers, making them the broadest category.
• 😀 In the quiz, the statement 'All negative numbers are integers' is false, as irrational negative numbers exist (e.g., -√2).
• 😀 The statement 'All natural numbers are real numbers' is true, as all natural numbers belong to the set of real numbers.

Q & A

What is the main topic discussed in the video?

The main topic is the set of real numbers and its subsets, which include rational numbers, integers, natural numbers, and irrational numbers.

How are rational numbers defined?

Rational numbers are those that can be written as fractions, such as 3/10, 13/5, or even integers and natural numbers when expressed as fractions with a denominator of 1.

What are irrational numbers?

Irrational numbers cannot be expressed as fractions and have non-terminating, non-repeating decimal expansions, like √2 or π.

What is the relationship between rational and irrational numbers?

Rational numbers can be written as fractions, while irrational numbers cannot. Together, they form the set of real numbers.

Can integers and natural numbers be considered rational numbers?

Yes, integers and natural numbers can be considered rational numbers because they can be written as fractions, such as 3 (3/1) or -2 (-2/1).

What are examples of irrational numbers given in the video?

Examples of irrational numbers include √2, π (approximately 3.1415…), and non-repeating decimals like 1.2345678910...

What is a Venn diagram used for in this lesson?

The Venn diagram is used to show how different subsets of numbers (rational, integers, natural, and irrational) are related and included within the real number system.

What does it mean that rational numbers can form periodic and terminating decimals?

Rational numbers can have decimals that either repeat (periodic) or terminate. For example, 1/3 gives a repeating decimal (0.333...), and 1/2 gives a terminating decimal (0.5).

Why are irrational numbers described as 'anti-heroes' in the video?

Irrational numbers are described as 'anti-heroes' because, unlike rational numbers that form neat fractions, they don't fit into the easy structure of fractions and have non-repeating, non-terminating decimals.

What are the correct answers to the interactive question about real numbers in the video?

The correct answers are: 'Statement 1' is false (because negative numbers can be irrational), 'Statement 2' is true (natural numbers are real numbers), and 'Statement 3' is true (real numbers can be rational or irrational).