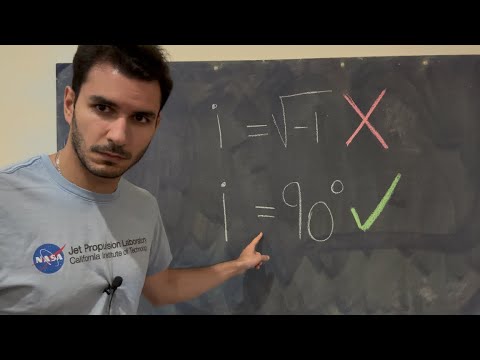Bilangan Kompleks • Part 2: Bilangan Imajiner

Summary

This video tutorial explains imaginary numbers and their role in solving quadratic equations. It covers the definition of imaginary numbers as roots of negative numbers (represented as 'i') and shows how they are used in solving quadratic equations, especially when the discriminant is negative. Through various examples, the video demonstrates how to express negative square roots in terms of 'i' and solve quadratic equations using both factorization and the quadratic formula. The video provides clear explanations, making complex concepts accessible for learners.

Takeaways

• 😀 Imaginary numbers are defined as the square roots of negative numbers, represented by the symbol 'i', where i = √-1.
• 😀 The discriminant (D) in a quadratic equation helps determine whether the roots are real or imaginary.
• 😀 When the discriminant is negative (D < 0), the solutions of the quadratic equation are imaginary.
• 😀 The quadratic formula is used to find the solutions of quadratic equations: x = (-b ± √D) / 2a.
• 😀 Imaginary numbers cannot be represented on the real number line, but they are essential for solving equations with negative discriminants.
• 😀 To express square roots of negative numbers in terms of imaginary numbers, you break them down using 'i'. For example, √-9 = 3i.
• 😀 Imaginary numbers are used to simplify the solutions of quadratic equations where real solutions do not exist.
• 😀 Example: For the equation x² + 5 = 0, the solution is x = ±√5i.
• 😀 When the equation involves fractions, such as √-1/4, it can be expressed as 1/2i.
• 😀 Complex quadratic equations can be solved using the quadratic formula, even when the discriminant leads to negative values, resulting in imaginary solutions.
• 😀 The solutions to more complex quadratic equations, like 3x² + 6x + 5 = 0, involve imaginary roots such as x = -1 ± 1/3√6i.

Q & A

What is an imaginary number?

An imaginary number is defined as the square root of a negative number. It is represented by the symbol 'i', where 'i = √-1'. These numbers are not represented on the real number line.

What does the symbol 'i' represent in complex numbers?

'i' represents the square root of -1, i.e., 'i = √-1'. It is used to express imaginary numbers in algebraic equations.

How does the discriminant relate to imaginary roots in quadratic equations?

In a quadratic equation of the form 'ax² + bx + c = 0', if the discriminant 'D = b² - 4ac' is less than 0, the equation has imaginary roots. This means the square root of a negative number, which leads to the inclusion of 'i' in the solutions.

How can we express the square root of a negative number as an imaginary number?

To express the square root of a negative number as an imaginary number, we factor the negative number into a positive part and -1. Then, we use 'i' to represent the square root of -1. For example, √-9 can be written as √9 * √-1 = 3i.

What is the quadratic formula used for solving quadratic equations?

The quadratic formula is used to find the roots of a quadratic equation. It is given by 'x = (-b ± √(b² - 4ac)) / 2a'. This formula is applied when solving equations of the form 'ax² + bx + c = 0'.

What happens when the discriminant is negative in the quadratic formula?

When the discriminant (b² - 4ac) is negative, the square root of a negative number is taken, which results in imaginary solutions. These solutions are expressed using 'i'.

In the example '√-9', how is the solution simplified?

The square root of -9 is simplified by breaking it down into √9 * √-1. √9 equals 3, and √-1 is represented by 'i'. So, √-9 becomes 3i.

How would you express '√-1/4' in terms of imaginary numbers?

To express √-1/4 in terms of imaginary numbers, we break it down as √(1/4) * √(-1). The square root of 1/4 is 1/2, and √(-1) is 'i'. Thus, √-1/4 becomes (1/2)i.

How do you solve a quadratic equation like 'x² + 5 = 0'?

To solve x² + 5 = 0, subtract 5 from both sides to get x² = -5. Then, take the square root of both sides: x = ±√(-5). This can be expressed as x = ±√5 * √-1 = ±√5i.

What is the solution to the quadratic equation '3x² + 6x + 5 = 0' using the quadratic formula?

For the equation 3x² + 6x + 5 = 0, we apply the quadratic formula. The discriminant is calculated as 36 - 60 = -24. The roots are x = (-6 ± √-24) / 6. Simplifying this, we get x = -1 ± (√6)i / 3, or x = -1 ± (1/3)√6i.