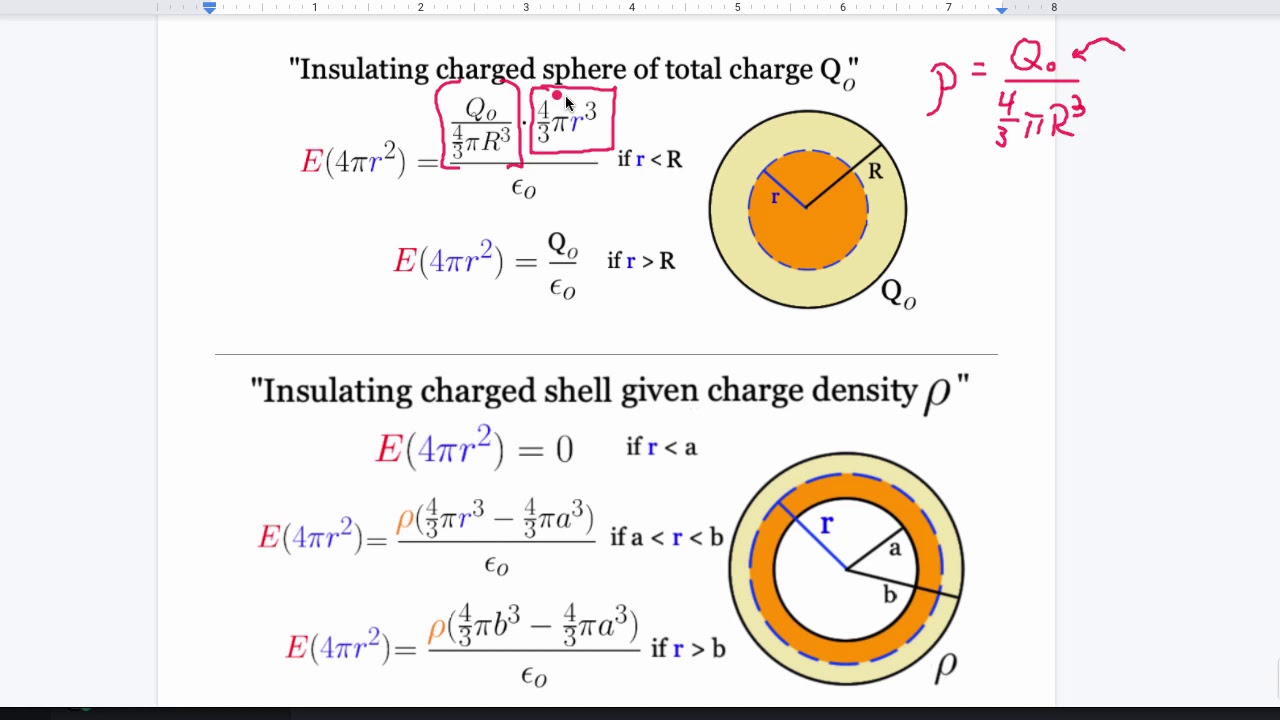University Physics Lectures, Gauss's Law and Applications

Summary

This lecture covers Gauss's Law and its applications. The instructor explains how the electric flux through a spherical Gaussian surface can be determined using Coulomb's Law, where the flux depends on the charge inside the surface and is independent of the shape of the surface. The discussion highlights the relationship between electric fields and flux, including examples of field lines entering and exiting different surfaces. The key takeaway is that the flux through any surface surrounding a point charge is proportional to the charge enclosed, and the net flux is zero when no charge is inside the surface.

Takeaways

• 😀 Gauss's law is applicable when a charge is placed inside a spherical Gaussian surface, resulting in an electric field that is normal to the surface.
• 😀 The electric flux through the surface is derived using the formula E·A = EA cos(θ), where θ is 0 degrees, making cos(0) = 1.
• 😀 Coulomb's law is used to calculate the electric field (E = kEq / r^2), where k is Coulomb's constant (8.99 x 10^9 N·m²/C²).
• 😀 The electric flux is calculated by integrating E·dA, with the surface integral over a sphere resulting in 4πR², representing the sphere's surface area.
• 😀 By substituting Coulomb's constant into the equation, the electric flux can be expressed as Q / ε₀, where ε₀ is the permittivity of free space.
• 😀 The net electric flux through any closed surface surrounding a point charge is always Q / ε₀, independent of the shape of the surface.
• 😀 If a charge is outside the surface, the electric flux through the surface is zero because the field lines entering and leaving the surface cancel each other out.
• 😀 When analyzing electric flux in different scenarios, such as with charges inside various surfaces (S, S'), the flux depends on the net charge inside the surface.
• 😀 If the net flux through a Gaussian surface is zero, the net charge inside the surface could still be zero or consist of charges that cancel each other out.
• 😀 Gauss's law can be applied to different charge distributions, and the electric flux is calculated using E·dA, which varies depending on the angle between E and dA.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.