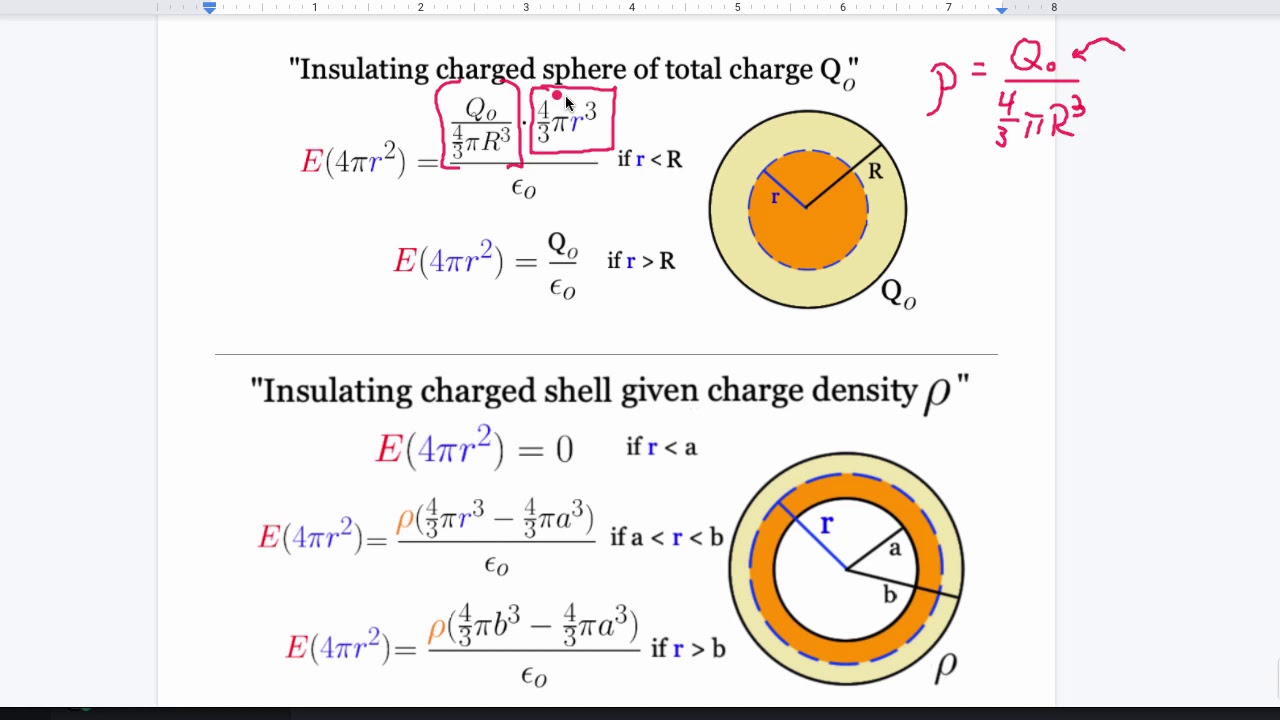3.1.1 Introduction to Laplace's Equation
Summary
TLDRThis chapter delves into electrostatics, exploring Coulomb's law, Gauss's law, and electric potential. It covers the calculation of electric fields and potentials for static charges, using integral and differential forms. The chapter introduces Laplace's equation, a key mathematical tool in electrostatics, highlighting its application in regions with no charge. Solutions to Laplace's equation, known as harmonic functions, are discussed for their relevance in various fields such as thermodynamics and gravitational fields. The chapter emphasizes mathematical techniques for solving complex electrostatic problems, offering valuable insights for students tackling physics challenges.
Takeaways
- 😀 The previous chapter focused on discovering the force on a particle from static, non-moving source charges.
- 😀 Coulomb's law was used to derive the electric field, which involves a complex integral over charge density.
- 😀 Gauss's law, which states that the flux of the electric field through a surface equals the enclosed charge over epsilon, is introduced as a simpler way to handle electric field calculations.
- 😀 The divergence of the electric field vector equals charge density divided by epsilon (Gauss's law in differential form).
- 😀 The electric field vector is related to the scalar potential function V, which simplifies calculations by avoiding vector calculus.
- 😀 The formula for calculating the potential involves an integral of 1/R, which is simpler to solve compared to other forms.
- 😀 Some charge distributions lead to hard integrals, and in such cases, a better approach or method may be needed.
- 😀 Conductors introduce a challenge, as charge density may not be known upfront, requiring additional techniques to determine it.
- 😀 Poisson's equation, or Laplace's equation in regions with no charge, is useful for solving electrostatic problems involving charge density and potential.
- 😀 Solutions to Laplace's equation, which are called harmonic functions, are crucial in solving many physical problems, from electrostatics to thermodynamics and gravitational fields.
- 😀 This chapter involves solving partial differential equations, with applications to various scientific domains, making it a more mathematical and problem-solving-focused chapter.
Q & A
What is the main focus of the last chapter discussed in the transcript?
-The last chapter focused on discovering the force on a particle due to static source charges that aren't moving, and it introduced Coulomb's law and Gauss's law as tools for solving electrostatic problems.
What is Coulomb's law, and how does it relate to electric fields?
-Coulomb's law defines the force between two point charges, and it is used to create the electric field by relating the charge distribution and distance. However, integrating it directly is often complex.
What is Gauss's law, and how is it useful in electrostatics?
-Gauss's law states that the electric flux through a surface is equal to the total charge enclosed within that surface divided by the permittivity of free space (ε₀). It simplifies solving electrostatic problems with high symmetry.
What does the differential form of Gauss's law state?
-The differential form of Gauss's law states that the divergence of the electric field (∇·E) is equal to the charge density (ρ) divided by ε₀, which is useful in analyzing localized regions of space.
How is the electric field related to the potential?
-The electric field (E) is the negative gradient of the potential (V), meaning E = -∇V. This relation allows the electric field to be derived from the scalar potential.
What is the advantage of using the potential in solving electrostatic problems?
-Using the potential simplifies the problem by turning vector equations into scalar ones, making it easier to compute, especially when dealing with symmetric charge distributions.
What equation is used to solve for the potential, and why is it preferred in some cases?
-The equation used to solve for the potential is the integral of 1/R times the charge density (ρ). This equation is preferred because the integral of 1/R is often simpler to solve than vector-based calculations.
What challenges arise when solving electrostatic problems involving conductors?
-One of the challenges with conductors is that the charge density cannot always be determined in advance. This requires additional methods or assumptions to derive the charge distribution.
What is Poisson's equation, and how is it used in electrostatics?
-Poisson's equation relates the Laplacian of the potential to the charge density. It is used to solve for the potential in regions where charge density is present.
What is Laplace's equation, and when is it applicable?
-Laplace's equation is a special case of Poisson's equation where the charge density is zero. It is useful in regions of space without any charges and can help solve for the potential in such areas.
What are harmonic functions, and what role do they play in solving electrostatic problems?
-Harmonic functions are the solutions to Laplace's equation. They are important in electrostatics because they describe the potential in charge-free regions, and their properties can be used to solve complex problems in various fields like thermodynamics, gravitation, and magnetism.
What types of problems can be solved using knowledge of harmonic functions and Laplace's equation?
-Harmonic functions and Laplace's equation are used in a wide range of problems, including electrostatics, thermodynamics, gravitational fields, magnetism, and other areas where solutions to partial differential equations are needed.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)