Pascal's Principle
Summary
TLDRThis video explains Pascal's Principle, which states that applied pressure is equally transmitted throughout a contained fluid, provided the fluid is incompressible. The principle is demonstrated using syringes, showing how pressure applied to one syringe is transferred to another. The concept of pressure, force, and area is explored, with a focus on hydraulics systems like lifts, brakes, and elevators. Additionally, the script covers the importance of pressure at the same height and introduces the hydrostatic equation, which accounts for pressure variations with depth.
Takeaways
- 😀 Pascal's principle states that applied pressure is transmitted equally throughout a contained fluid.
- 😀 The fluid must be incompressible for Pascal's principle to apply.
- 😀 A simple demonstration using two syringes and water shows Pascal's principle in action.
- 😀 When pressure is applied to one syringe, the other syringe moves due to the incompressibility of the fluid.
- 😀 The pressure applied to the fluid is transmitted equally, meaning the pressure in both syringes is the same.
- 😀 Pressure is defined as force divided by area (P = F/A), which helps explain the behavior in the syringes.
- 😀 The syringe with a smaller area requires less force to achieve the same pressure as the larger syringe.
- 😀 Pascal's principle is commonly used in hydraulic systems, such as hydraulic lifts, elevators, and brakes.
- 😀 Hydraulic systems use smaller areas to lift larger objects by transmitting pressure efficiently.
- 😀 Pressure varies with depth, meaning if points are at different heights, the hydrostatic equation (P = ρgh) must be used to calculate pressure differences.
- 😀 The hydrostatic equation takes into account density (ρ), gravitational acceleration (g), and height (h) when calculating pressure at different depths.
Q & A
What does Pascal's principle state?
-Pascal's principle states that applied pressure is transmitted equally throughout a contained fluid.
What condition must be met for Pascal's principle to apply?
-For Pascal's principle to apply, the fluid must be incompressible.
How can Pascal's principle be demonstrated?
-Pascal's principle can be demonstrated using a simple system of two syringes, tubing, and water. When pressure is applied to one syringe, the other syringe moves due to the incompressible nature of the fluid.
Why is it harder to push down the larger syringe in the demonstration?
-It is harder to push down the larger syringe because, due to Pascal's principle, the pressure is equal at both syringes, and the larger syringe has a larger area, requiring more force to achieve the same pressure.
What is the mathematical relationship for pressure?
-Pressure equals force divided by area, or P = F/A.
Why does the smaller syringe require less force in the demonstration?
-The smaller syringe has a much smaller area, so it requires less force to achieve the same pressure compared to the larger syringe.
What are some common applications of Pascal's principle?
-Some common applications of Pascal's principle include hydraulic lifts, elevators, and brakes.
How do hydraulic systems take advantage of Pascal's principle?
-Hydraulic systems use smaller areas to apply force, which can lift larger objects. This is an example of how Pascal's principle is used in practical systems.
When does pressure vary in a fluid?
-Pressure varies with depth in a fluid, meaning that at different depths, the pressure may be different.
What additional consideration must be taken when points of interest are at different heights?
-When points of interest are at different heights, you must also take into account the hydrostatic equation, which states that pressure equals height times density times gravity (P = h * ρ * g).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
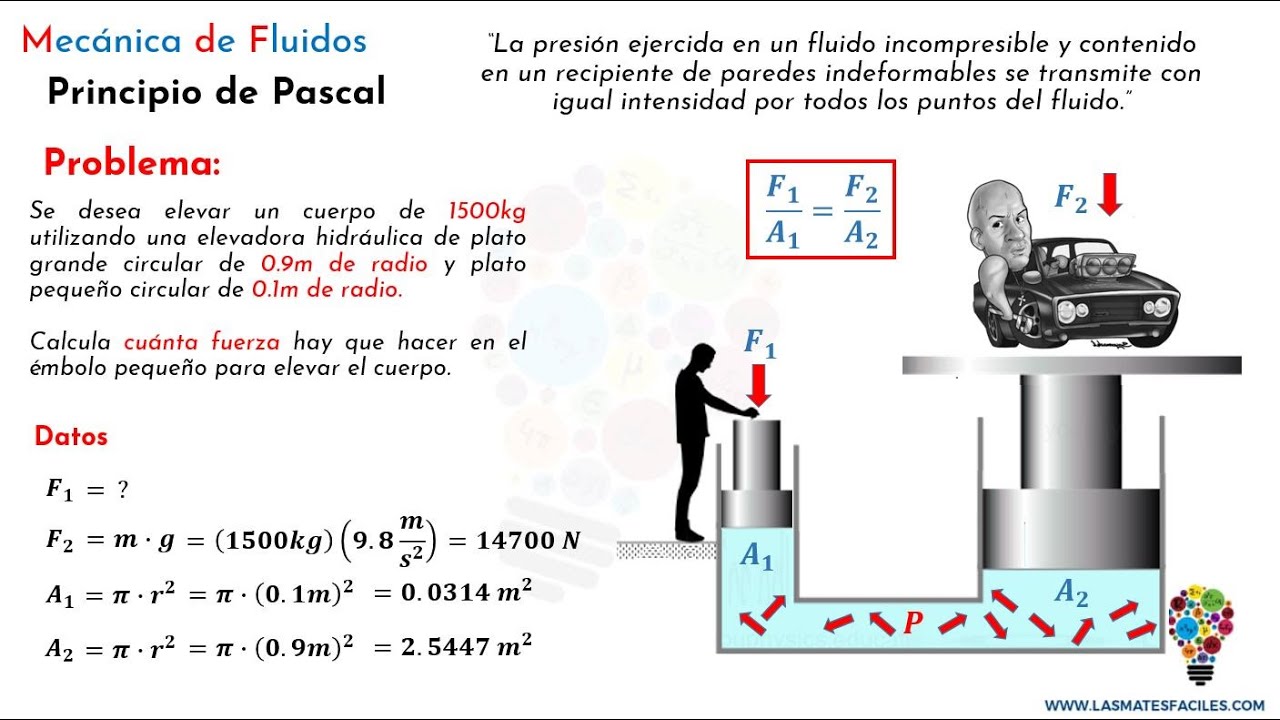
Principio de Pascal. Explicación

22. Física e Introducción a la Biofísica. Principio de Pascal

I fluidi, la pressione, la legge di Pascal e il torchio idraulico

FISIKA Kelas 11 - Hukum Pascal | GIA Academy

How a hydraulic jack works (3D Animation | Pascal Principle)

Hukum Pascal ( Tekanan Zat Dan Penerapannya Dalam Kehidupan Sehari-hari )
5.0 / 5 (0 votes)