Rumus Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRIn this video, the presenter discusses the concept of inverse functions, focusing on how to determine the inverse of a given function using quick formulas. The video covers three main cases: when the function is of the form x + a, ax, or a rational expression (ax + b)/(cx + d). The presenter demonstrates the application of these formulas through examples and provides a step-by-step guide to solving inverse function problems. Additionally, the video includes a detailed proof of the formulas to ensure their validity and ends with a practice problem for viewers.
Takeaways
- 😀 Inverse functions are the reverse or opposite of the original function, switching the roles of x and y.
- 😀 The first formula for finding the inverse is for a function of the form f(x) = x + a, where the inverse is f^(-1)(x) = x - a.
- 😀 The second formula is for functions in the form f(x) = a * x, with the inverse being f^(-1)(x) = x / a.
- 😀 The third formula applies to rational functions of the form f(x) = (ax + b) / (cx + d), where the inverse is f^(-1)(x) = (-dx + b) / (cx - a).
- 😀 Inverse functions can be verified by substituting the inverse back into the original function and checking if the result is x.
- 😀 For a simple example, if f(x) = x + 3, the inverse is f^(-1)(x) = x - 3.
- 😀 For the function f(x) = 2x, the inverse is f^(-1)(x) = x / 2.
- 😀 To find the inverse of more complex functions, like f(x) = (2x + 3) / (x - 5), apply the third formula by swapping values of a and d, and multiplying by negative.
- 😀 The process to derive the inverse involves changing f(x) to y, isolating x, and then swapping variables to find the inverse.
- 😀 In all cases, once the inverse is derived, it can be verified using the standard process to ensure accuracy.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of inverse functions and how to calculate the inverse of various types of functions.
What is the first formula for determining the inverse of a function?
-The first formula is for functions of the form f(x) = x + a, where the inverse function is f⁻¹(x) = x - a.
How is the inverse function derived for a function of the form f(x) = a * x?
-For a function of the form f(x) = a * x, the inverse is f⁻¹(x) = x / a, as the inverse operation is division.
What is the inverse of a function of the form f(x) = (a * x + b) / (c * x + d)?
-For a function in the form f(x) = (a * x + b) / (c * x + d), the inverse function is f⁻¹(x) = (-d * x + b) / (c * x - a), where the coefficients a, b, c, and d are swapped and adjusted with negative signs.
How does the inverse of f(x) = x + 3 work based on the formulas?
-Using the first formula, for f(x) = x + 3, the inverse function would be f⁻¹(x) = x - 3, as the inverse of addition is subtraction.
Why is it important to validate the inverse of a function?
-It is important to validate the inverse of a function to ensure that the derived inverse function truly satisfies the inverse relationship and works for all possible cases.
In the example where f(x) = 2x, how is the inverse determined?
-For the function f(x) = 2x, the inverse is f⁻¹(x) = x / 2, since the inverse operation of multiplication by 2 is division by 2.
How is the inverse of the rational function f(x) = (2x + 3) / (x - 5) calculated?
-The inverse of the rational function f(x) = (2x + 3) / (x - 5) is calculated by swapping the coefficients and multiplying by negative signs, resulting in f⁻¹(x) = (5x + 3) / (x - 2).
What steps are involved in the detailed process of calculating the inverse of f(x) = (2x + 3) / (x - 5)?
-The detailed process involves replacing f(x) with y, cross-multiplying to eliminate the fraction, and solving for x. The resulting equation is then simplified, and y is replaced with x to find the inverse function.
How can we ensure that the derived inverse function is correct?
-To ensure the derived inverse function is correct, we can verify it by checking if applying the original function and its inverse results in the identity function, i.e., f(f⁻¹(x)) = x and f⁻¹(f(x)) = x.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Fungsi Invers Part 1 ||Materi, Soal & Pembahasan||

Fungsi Komposisi dan Fungsi Invers SMA/MA/SMK
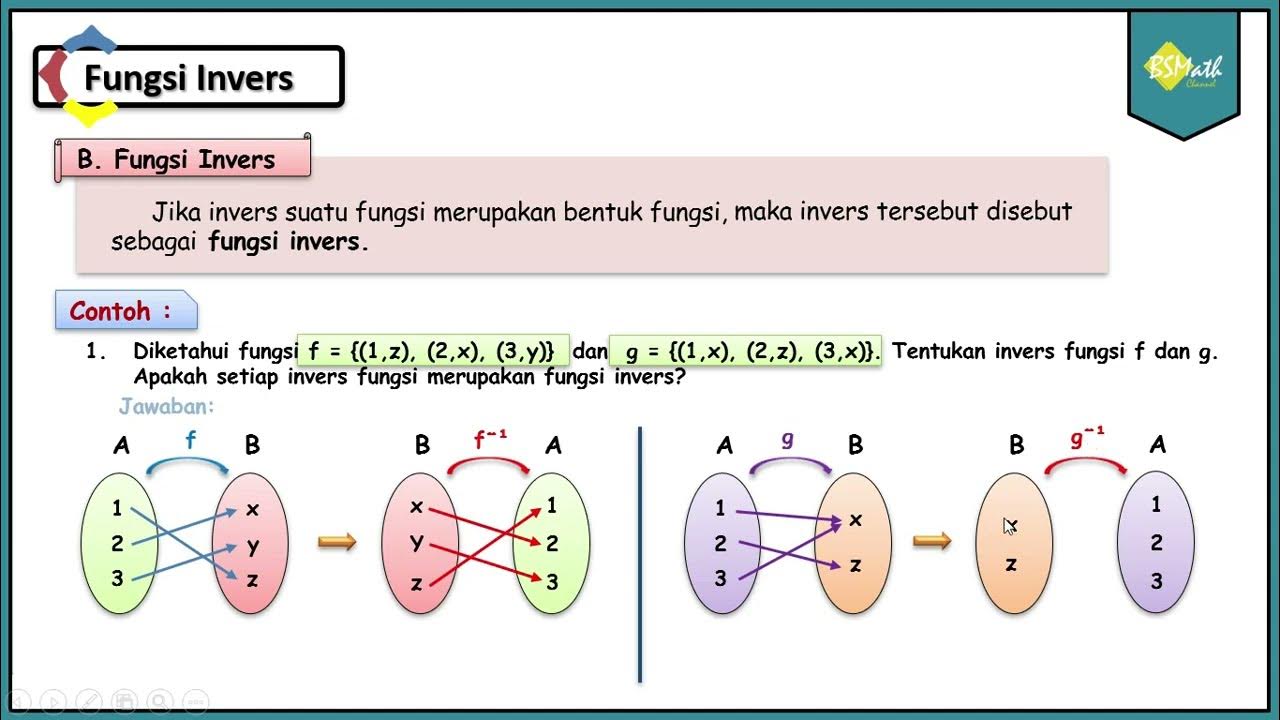
Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka

Derivatives of inverse functions | Advanced derivatives | AP Calculus AB | Khan Academy

Komposisi Fungsi Part 3 - Fungsi invers dan Sifat-sifatnya [ Matematika Wajib Kelas X ]

REPRESENTATIONS OF AN INVERSE FUNCTIONS | General Mathematics | Quarter 1 - Module 13
5.0 / 5 (0 votes)