Pivot de #Gauss : résoudre les systèmes d'équations a trois inconnues

Summary

In this video, the process of solving a system of equations using the left pivot method is explained step by step. The method begins by choosing a pivot in the first equation, followed by eliminating variables to create a triangular system. The solution is found by substituting known values for Z and Y into the system, ultimately solving for X, Y, and Z. The video emphasizes the simplicity and clarity of the left pivot method, with the same system being solved through the substitution method in the next video. Viewers are encouraged to engage and subscribe for more educational content.

Takeaways

• 😀 The video explains how to solve a system of equations using the left pivot method.
• 😀 The left pivot method is introduced as a way to simplify a system into a triangular form.
• 😀 It is recommended to choose the simplest coefficient for the pivot to make the calculation easier.
• 😀 The script emphasizes the importance of multiplying the pivot to eliminate terms from other equations.
• 😀 After applying the pivot, the system is transformed into a triangular form, which simplifies further solutions.
• 😀 The method involves performing operations like multiplying equations and combining them to eliminate variables step by step.
• 😀 The process of solving is shown through a detailed example, where pivots are chosen carefully to reduce the system.
• 😀 The video also highlights how to find the value of each variable by substituting known values into the equations.
• 😀 After solving for the last variable (Z), substitution is used to find the values for other variables (Y, X).
• 😀 The final solution of the system is a triplet (X, Y, Z), providing the complete set of solutions to the system.
• 😀 The script concludes by indicating that this method can be used for any system of equations and suggests the next video will cover substitution in more detail.

Q & A

What method is used in the video to solve the system of equations?

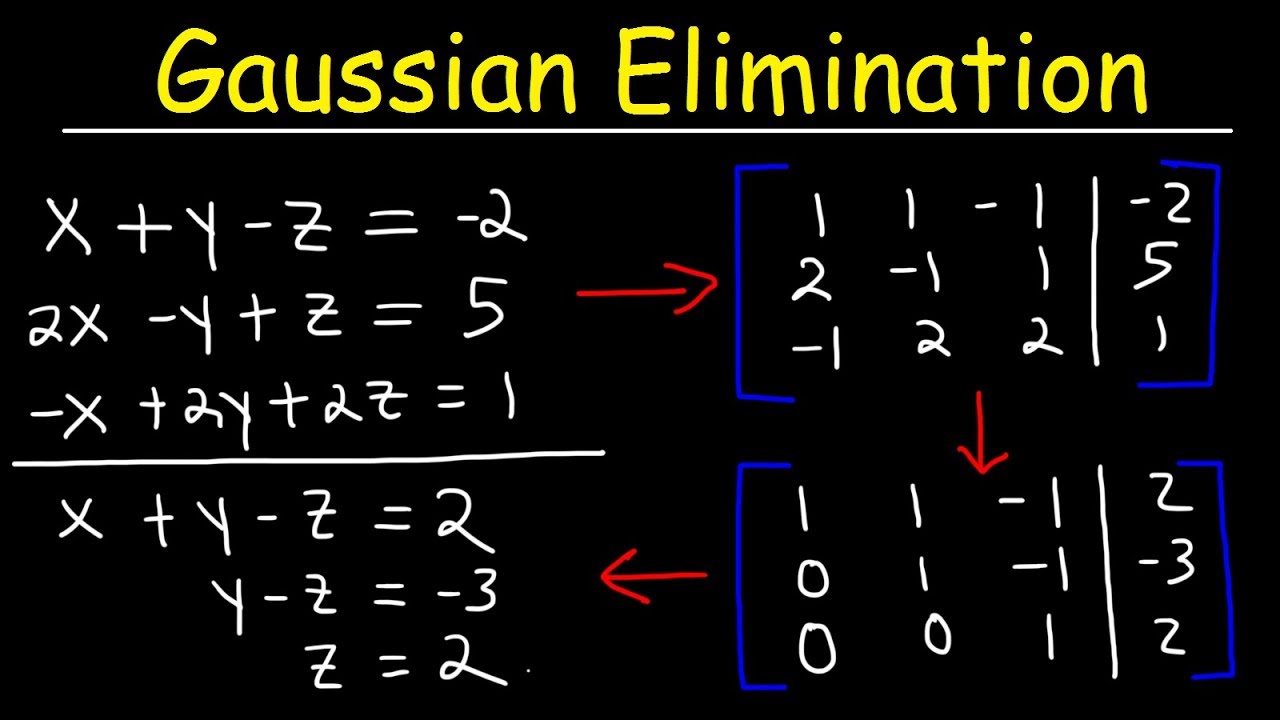
The video demonstrates solving the system of equations using the **left pivot method (pivot de gauche)**, which involves converting the system into a triangular form to simplify solving the variables.

What is the purpose of pivoting in the left pivot method?

The purpose of pivoting is to eliminate variables from the system by multiplying the pivot equation with appropriate values and adding it to the other equations, ultimately creating a simpler triangular system.

Why is the choice of the pivot important in the left pivot method?

The pivot is crucial because it simplifies the process of eliminating variables. The chosen pivot should ideally have the smallest or most straightforward coefficient to make calculations easier, such as selecting the coefficient of `X` in the first equation.

How is the first equation pivoted in the video?

The first equation is used as the pivot, and the other equations are manipulated by multiplying the pivot equation by specific values (like -2) to eliminate the `X` variable from the second and third equations.

What is the result after pivoting the first equation in the video?

After pivoting, the second and third equations are modified, with the goal of eliminating the `X` variable and simplifying the system to a triangular form, making it easier to solve for other variables like `Y` and `Z`.

What does the triangular form of a system of equations represent?

The triangular form of a system represents a simplified structure where variables can be solved progressively, starting with the last variable (usually `Z`), followed by `Y`, and then `X`, making the system easier to solve step by step.

How are the variables `Z` and `Y` solved in the triangular system?

In the triangular system, the value of `Z` is solved first, followed by `Y`. After finding `Z = -2`, it is substituted into the equation for `Y`, yielding `Y = 2`. The value of `Y` is then substituted into the equation for `X` to find `X = 1`.

What are the final values of the variables `X`, `Y`, and `Z`?

The final values of the variables are: `X = 1`, `Y = 2`, and `Z = -2`.

What is the final solution of the system in terms of the variables?

The final solution to the system of equations is the triplet `(X, Y, Z) = (1, 2, -2)`, which is the set of values that satisfy all three equations.

What is the advantage of using the left pivot method to solve a system of equations?

The left pivot method provides a structured approach to solving systems of linear equations by transforming the system into a simpler triangular form, which makes it easier to isolate and solve for each variable one by one.