Lec-62: Introduction to Red-Black Tree | Data Structure for Beginners
Summary
TLDRIn this video, the concept of Red-Black Trees is explained in detail, emphasizing their importance for competitive exams and interviews. A Red-Black Tree is a self-balancing binary search tree that ensures logarithmic time complexity for operations like search, insertion, and deletion. The key properties of a Red-Black Tree include each node being either red or black, the root being black, no adjacent red nodes, and maintaining a consistent black depth across paths. The video also highlights the structure and rules that govern Red-Black Trees, preparing viewers for upcoming lessons on insertion techniques.
Takeaways
- 😀 A Red-Black Tree is a self-balancing binary search tree where each node is either Red or Black.
- 😀 The root of a Red-Black Tree is always Black, which is a key property to maintain balance.
- 😀 Red nodes cannot have Red children, meaning no two adjacent nodes can both be Red.
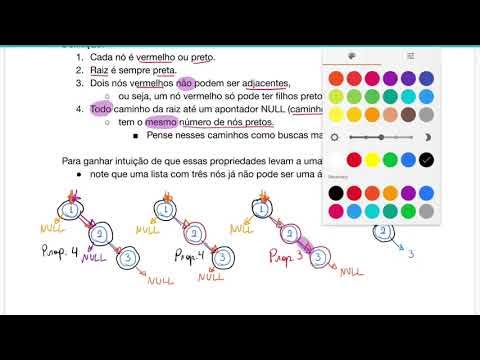
- 😀 The Red-Black Tree ensures that all paths from any node to its leaf nodes contain the same number of Black nodes.
- 😀 Leaf nodes (also known as NIL nodes) are always Black and do not store any data.
- 😀 Each node in the tree has a color, which can be represented by a single bit: 1 for Red and 0 for Black.
- 😀 A Red-Black Tree is an extension of the Binary Search Tree (BST) with added balancing properties for efficient operations.
- 😀 In a Red-Black Tree, every path from the root to any leaf contains the same number of Black nodes, ensuring balance.
- 😀 The primary operations like search, insert, and delete in a Red-Black Tree can all be performed in O(log n) time complexity.
- 😀 The balance of the tree is maintained using five key properties, with emphasis on the root's color, Red node restrictions, and Black depth.
Q & A
What is a Red-Black Tree?
-A Red-Black Tree is a self-balancing binary search tree where each node is colored either red or black. The color properties help maintain balance in the tree, ensuring that operations like search, insert, and delete take logarithmic time (O(log n)) in the worst case.
How does a Red-Black Tree differ from a regular Binary Search Tree (BST)?
-While both Red-Black Trees and regular BSTs are binary search trees, the Red-Black Tree has additional color-coding and balancing properties. These properties ensure the tree remains balanced, avoiding the skewing that can occur in a regular BST, thereby ensuring O(log n) time complexity for operations.
What is the role of the 'color' in a Red-Black Tree?
-The color of each node (either red or black) is used to maintain the balance of the tree. The color helps enforce rules such as preventing two red nodes from being adjacent and ensuring an equal number of black nodes on all paths from a node to its leaf nodes.
Can the root of a Red-Black Tree be red?
-No, the root of a Red-Black Tree must always be black. This is a fixed property and helps maintain the tree's balance from the start.
What happens if two red nodes are adjacent in a Red-Black Tree?
-If two red nodes are adjacent, the tree violates the Red-Black Tree property that no two red nodes can be adjacent. This imbalance must be corrected through rotations and color adjustments during insertion or deletion operations.
What is the Black Depth Property in a Red-Black Tree?
-The Black Depth Property states that every path from a node to its descendant leaf nodes must contain the same number of black nodes. This ensures the tree remains balanced by limiting the height of paths, keeping operations efficient.
What is the significance of leaf nodes in a Red-Black Tree?
-Leaf nodes in a Red-Black Tree (which are also known as null or nil nodes) are always black and do not store any data. They are important for maintaining the tree structure and ensuring balance but do not participate in the data search process.
What happens when you start traversing from a node in a Red-Black Tree?
-When you start traversing from any node in a Red-Black Tree, the number of black nodes encountered on all paths to leaf nodes must be the same. If the black node count differs between paths, the tree is not a valid Red-Black Tree.
Why is the Red-Black Tree considered efficient for search operations?
-The Red-Black Tree is considered efficient for search operations because of its self-balancing properties. By ensuring that the tree's height is always logarithmic (O(log n)), it guarantees that search, insert, and delete operations can all be performed efficiently, even in the worst case.
What is the significance of the 'Red Node Property' in a Red-Black Tree?
-The Red Node Property dictates that no red node can have a red child. This prevents adjacent red nodes, maintaining the balance of the tree and ensuring that paths from any node to its leaf nodes do not become too long or unbalanced, which would otherwise degrade performance.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

L-7.3: Allocation Methods in operating system in hindi | Contiguous vs NonContiguous
Aula 05.1 - Árvores Rubro Negras: Definição (AED2)

Lec-61: ARP Explained- Address Resolution Protocol | Network Layer

General Characteristics Of Ionic Bonding | Chemical Bonding -1 | BSc.1st Semester Chemistry Notes |

L-4.13: Bellman Ford Algorithm | Dijkstra's Vs Bellman Ford | Single Source Shortest Path

Types of Testing in Software Engineering | Levels of Testing
5.0 / 5 (0 votes)