2025 IYPT 11. Spring Hysteresis Unraveling Dynamics of Spring Systems!
Summary
TLDRThis study explores the dynamic behavior of a mass-spring system with two identical, linear springs symmetrically attached to a v-shaped mass. By applying an adjustable force, the system exhibits fascinating motion patterns that depend on the force's history. The research delves into various bifurcations, such as saddle-node and pitchfork bifurcations, occurring as system parameters change. It also examines critical slowing down and hysteresis cycles near bifurcation points. Through theoretical analysis and detailed simulations, the study offers an in-depth understanding of stability, bifurcation, and the underlying principles driving this dynamic system.
Takeaways
- 😀 Two identical, linear springs are symmetrically attached to a v-shaped mass in the system.
- 😀 An adjustable external force is applied to the mass, influencing its motion in complex ways.
- 😀 The motion patterns of the system depend on the history of the force variation.
- 😀 The study explores the dynamic behavior of the system, combining theoretical analysis and computational simulations.
- 😀 The system demonstrates how continuous parameter changes can lead to critical transitions or tipping points.
- 😀 Key bifurcations such as saddle node and pitchfork bifurcations occur when varying the external force or spring separation.
- 😀 The system exhibits hysteresis cycles and critical slowing down near bifurcation points.
- 😀 The research provides a comprehensive analysis of bifurcation and stability in the mass-spring system.
- 😀 The study progresses from basic principles to advanced theoretical models for a deeper understanding of the system's behavior.
- 😀 The system's behavior is analyzed not only in terms of static conditions but also dynamic responses to varying parameters over time.
Q & A
What is the system described in the transcript?
-The system consists of two identical, linear springs symmetrically attached to a V-shaped mass, with an adjustable force applied to the mass.
What happens when the external force applied to the system is varied?
-Varying the external force leads to fascinating motion patterns that depend on the history of the force variation, showcasing complex dynamic behavior.
What are bifurcations, and which types are discussed in the study?
-Bifurcations refer to critical transitions in a system's behavior. The study discusses saddle-node and pitchfork bifurcations that occur when varying external forces or spring separation parameters.
What is meant by 'critical slowing down' in the context of the system?
-'Critical slowing down' refers to the phenomenon where the system’s response time increases significantly as it approaches a bifurcation point.
What are 'hysteresis cycles,' and how do they manifest in the system?
-Hysteresis cycles occur when the system exhibits different behavior depending on whether the parameters are increasing or decreasing. This phenomenon is observed as the system moves through different states in response to varying external forces.
What kind of transitions does the system demonstrate as it moves through bifurcation points?
-The system demonstrates transitions such as changes in stability and behavior as it approaches and passes through bifurcation points, with critical slowing down and hysteresis playing key roles in these transitions.
How does the study approach the analysis of this system's behavior?
-The study uses both theoretical analysis and detailed computational simulations to explore the dynamic behavior of the system and its bifurcations.
What are the implications of varying spring separation parameters in the system?
-Varying the spring separation parameters influences the occurrence of bifurcations, which in turn affect the stability and behavior of the system.
How do continuous changes in system parameters lead to critical transitions?
-Continuous changes in parameters like external force or spring separation can push the system to a tipping point, leading to sudden and significant changes in its behavior, known as bifurcations.
What is the focus of the study regarding the system’s stability and bifurcations?
-The study provides an in-depth analysis of the bifurcation and stability in the system, starting from basic principles and progressing to more advanced theoretical models.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Simple Harmonic Motion Introduction(SHM) via a Horizontal Mass-Spring System

Oscillations Demo: Mass Spring System

Springs & Hooke's Law - GCSE & A-level Physics (full version)

How to determine the spring constant

Praktikum Fisika 1 Getaran pada Pegas (Modul 7)
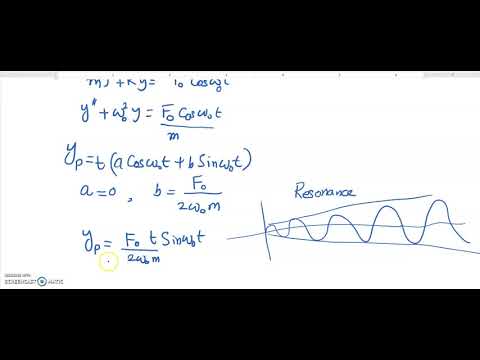
Modeling Forced Oscillations of Mass Spring System clip 3
5.0 / 5 (0 votes)