Electrical Resistivity and Conductivity - Superconductors & Supercapacitors - Engineering Physics 1

Summary

In this lecture, we delve into the concepts of resistivity and conductivity, starting with the derivation of the resistance formula based on a conductor’s length and cross-sectional area. We explore how resistivity (ρ) relates to resistance (R) and its inverse relationship with conductivity (σ). The video also explains the SI units of resistivity and conductivity, and the impact of temperature on resistance, introducing the equation that describes this dependency. Overall, the lecture provides foundational knowledge for understanding how materials resist or conduct electric current, and how these properties change with temperature.

Takeaways

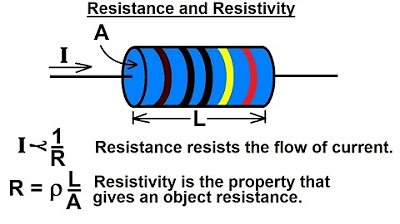
• 😀 Resistance is proportional to the length of the conductor (R ∝ L).
• 😀 Resistance is inversely proportional to the cross-sectional area of the conductor (R ∝ 1/A).
• 😀 The formula for resistance is R = ρ(L/A), where ρ is resistivity.
• 😀 Resistivity (ρ) is a constant of proportionality, and conductivity (σ) is the reciprocal of resistivity.
• 😀 The formula for conductivity is σ = L/A.
• 😀 The SI unit for resistivity (ρ) is ohm meter (Ω·m).
• 😀 The SI unit for conductivity (σ) is Siemens per meter (S/m).
• 😀 The temperature dependence of resistance is described by the equation: RT = R0(1 + αΔT).
• 😀 RT represents the resistance at a temperature T, R0 is the resistance at 0°C, α is the temperature coefficient of resistance, and ΔT is the temperature change.
• 😀 As temperature increases, the resistance of the conductor also increases, typically showing a linear relationship.
• 😀 The graph of resistance versus temperature is a straight line, similar to the equation y = mx + c, with R0 as the y-intercept.

Q & A

What is the relationship between resistance and the length of a conductor?

Resistance is directly proportional to the length of the conductor. As the length of the conductor increases, the resistance also increases.

How does the area of cross-section affect the resistance of a conductor?

Resistance is inversely proportional to the area of the cross-section of the conductor. A larger area allows current to flow more easily, thus reducing resistance.

What is the equation that relates resistance, resistivity, length, and area?

The equation is R = ρ * (L / A), where R is resistance, ρ is resistivity, L is the length, and A is the area of cross-section.

What is resistivity and how does it relate to conductivity?

Resistivity (ρ) is a property of the material that determines how much it resists the flow of electric current. Conductivity (σ) is the reciprocal of resistivity, meaning σ = 1 / ρ.

What is the relationship between resistivity and conductivity?

The relationship is given by ρ * σ = 1. This means that resistivity and conductivity are inversely related.

What are the SI units of resistivity and conductivity?

The SI unit of resistivity is Ohm meter (Ω·m), and the SI unit of conductivity is Siemens per meter (S/m).

How does temperature affect the resistance of a conductor?

Resistance increases with temperature. This temperature dependence can be expressed using the formula R_T = R_0 * (1 + α * ΔT), where R_T is the resistance at temperature T, R_0 is the resistance at a reference temperature, α is the temperature coefficient of resistance, and ΔT is the temperature change.

What does the temperature coefficient of resistance represent?

The temperature coefficient of resistance (α) represents how much the resistance of a material changes with a change in temperature. A positive α means resistance increases with temperature.

How can the temperature dependence of resistance be graphically represented?

The temperature dependence of resistance can be represented by a graph where resistance increases linearly as temperature increases. The graph typically shows a straight line, with R_0 being the offset.

Why is the concept of resistivity important in material science?

Resistivity is crucial in material science because it helps determine how materials will behave in electrical circuits, which is essential for selecting materials for conductors, insulators, and semiconductors.