Introductory Work due to Friction equals Change in Mechanical Energy Problem
Summary
TLDRIn this engaging physics lesson, students solve a problem involving the motion of a street hockey puck sliding to a stop due to friction. By applying the work-energy principle, they calculate the displacement of the puck, which initially moves with a velocity of -3.2 m/s. The class explores the relationship between friction, energy dissipation as heat and sound, and mechanical energy. Through a mix of humor, clarifications, and calculations, they ultimately determine the puck slides 0.87 meters before stopping, emphasizing the importance of magnitude in the displacement calculation.
Takeaways
- 😀 The initial velocity of the puck is -3.2 m/s, indicating it is moving to the left.
- 😀 The final velocity of the puck is zero, as it slides to a stop.
- 😀 The coefficient of kinetic friction (μk) between the puck and the surface is 0.60.
- 😀 The task is to determine the distance the puck slides, focusing on the magnitude of the displacement.
- 😀 The problem is solved using the equation for work due to friction, which equals the change in mechanical energy.
- 😀 There is no applied force acting on the puck while it slides; only friction does work.
- 😀 The initial mechanical energy is purely kinetic, and it is dissipated as heat and sound as the puck stops.
- 😀 The frictional force is calculated by multiplying the coefficient of kinetic friction (μk) by the normal force.
- 😀 To solve for the normal force, a free-body diagram is used, and it is found that the normal force equals the gravitational force on the puck.
- 😀 The displacement is calculated using the equation involving the coefficient of kinetic friction, gravitational acceleration, and the initial velocity squared, resulting in a displacement of 0.87 meters.
Q & A
Why is the initial velocity of the puck negative?
-The initial velocity is negative because the puck is moving to the left.
What equation is used to solve this problem, and why is it applicable?
-The equation used is the work due to friction equals the change in mechanical energy. It's applicable because friction is the only force doing work on the puck, and mechanical energy changes due to the conversion of kinetic energy into heat and sound.
What forces are involved in this problem, and how are they addressed in the equation?
-The forces involved are kinetic friction and gravity. The force of kinetic friction is calculated using the coefficient of kinetic friction and the normal force, which is equal to the puck's weight (mass times gravitational acceleration).
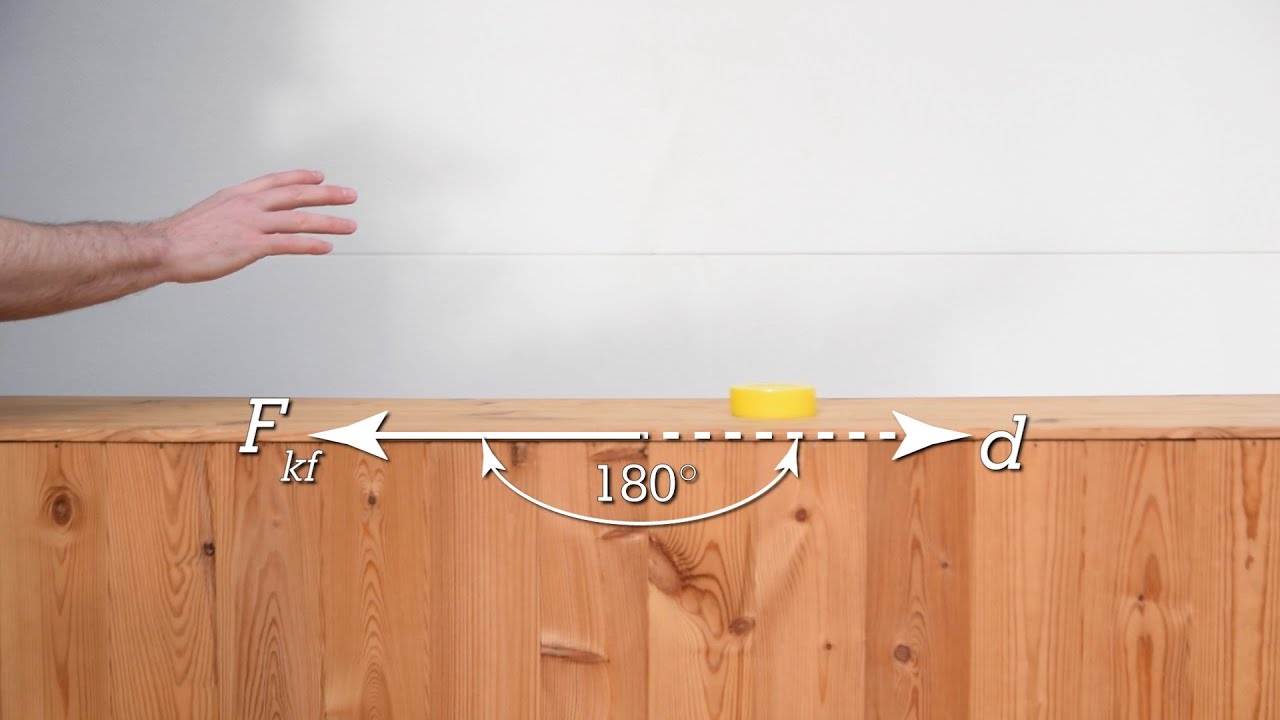
What is the significance of the angle (theta) in the work equation?
-The angle (theta) represents the direction between the force of kinetic friction and the displacement. Since the puck moves to the left and friction opposes this motion, theta is 180 degrees, making the cosine of theta equal to -1.
Why is the final mechanical energy of the puck zero?
-The final mechanical energy is zero because the puck comes to a stop, meaning its final kinetic energy is zero.
How does the kinetic energy of the puck change as it slides to a stop?
-The initial kinetic energy of the puck is converted into heat and sound due to friction, which dissipates the energy, causing the puck to stop.
Why does the displacement of the puck need to be positive even though the motion is to the left?
-The displacement is calculated as the magnitude of the distance traveled, which is always positive. The direction of the displacement (to the left) is not relevant for this particular problem, which only asks for the magnitude.
What role does the free body diagram play in solving for the normal force?
-The free body diagram helps identify the forces acting on the puck, particularly the normal force. By summing the forces in the vertical direction, we find that the normal force equals the gravitational force acting on the puck, which is equal to mass times acceleration due to gravity.
How is the force normal calculated in this problem?
-The force normal is calculated by summing the forces in the vertical direction, and since the puck does not move vertically, the net vertical force is zero. Therefore, the normal force equals the gravitational force, which is the mass of the puck times the acceleration due to gravity.
What is the final displacement of the puck, and how is it calculated?
-The final displacement is 0.87 meters. It is calculated using the equation: displacement = (velocity initial squared) / (2 * acceleration due to gravity * coefficient of kinetic friction). By substituting the known values, the displacement is found to be approximately 0.87 meters.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Past Board Exam Problem about Friction SOLVED! (Mechanics)

Friction: Crash Course Physics #6
Plano inclinado con rozamiento (Bachillerato)
Introduction to Mechanical Energy with Friction

FISICA! forza d’attrito, fisica attrito, attrito statico e dinamico, forza d’attrito esercizi

Introductory Rotational Equilibrium Problem
5.0 / 5 (0 votes)